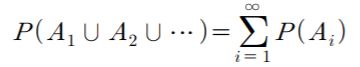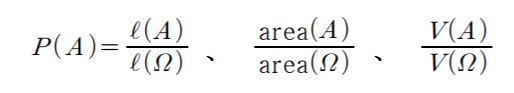【概率论基础】Probability | 数学性概率 | 统计性概率 | 几何概率 | 概率论三大公理
前言:
个人学习笔记,由于是国外教材,所以翻译的数学名词可能与国内教材上的有些许出入。
目录
前言:
0x00 概率的定义
0x02 概率的基本性质
0x03 概率公理化(axiomatic probability)
0x04 几何概率(geometric probability)
0x00 概率的定义
概率(probability)
一场概率实验中,某事件发生A的可能性程度,0 和 1 之间表示的实数值,称为概率(probability)。
通常以以下三种方式定义概率:
① 数学性概率(事件概率)
② 统计性概率(事件概率)
③ 公理性概率
数学性概率(mathematical probablity)
假设概率实验中所有的结果都有相同的概率,如将样本空间 ![]() 中样本点个数标记为
中样本点个数标记为 ![]() 个。 A 中的样本点的数记为
个。 A 中的样本点的数记为 ![]() 个。
个。
我们称之为 —— 事件A的数学性概率(必须有限)
统计性概率(law of large number)
一场概率实验反复施行 ![]() 次,发生事件 A 的次数为
次,发生事件 A 的次数为 ![]() 时,事件A 称为相对频率(relative frequency):
时,事件A 称为相对频率(relative frequency):
缺陷:统计概率因实验次数而异。
大数法则(law of large number)
随着概率试验次数的增加,统计概率愈趋近于数学概率:
![]()
Example1:
(1)求1次抛硬幣正面朝上(記為H)的概率。
(2)通過抛10000次硬幣獲得如下結果,在此結果的基礎上計算出正面(H)出現的概率。
10000次,正面5017次,反面4983次![]()
(1) ![]()
(2) ![]()
Example2:
投幣三次,是正面的次數 i 為事件 Ai(i=0,1,2,3) 時,求該事件的概率。![]()
![]()
![]()
![]()
![]()
Example3:
连续抛两次骰子,第一次抛时出现的点数是3的倍数记为事件A,
第二次抛时出现的点数是3的倍数时记为事件B。
分别求出 P(A) 和 P(A∩B)![]()
A = { (3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }
B = { (1,3), (1,6), (2,3), (2,6), (3,3), (3,6),
(4,3), (4,6), (5,3), (5,6), (6,3), (6,6) }
A ∩ B = { (3,3), (3,6), (6,3), (6,6) }
0x02 概率的基本性质
理论:
对于下列AB事件,如下性质成立:
① ![]()
② ![]()
③ ![]()
④ ![]()
⑤ 如果 A 和 B 互斥,![]()
⑥ 如果 ![]() ,
, ![]()
⑥ 如果 ![]() ,
, ![]()
对于下列ABC事件 ,以下性质成立:
![]()
0x03 概率公理化(axiomatic probability)
标准空间 ![]() 定义所有事件的汇集
定义所有事件的汇集 ![]() 时,
时,
如果集合 ![]() 上定义的函数
上定义的函数 ![]()
满足以下三大公理:
我们所有的研究都是建立在概率是非负数的前提下的
(A2)![]()
所有可能的概率为1
如果事件互斥,它们交的概率为它们各自的概率之和
![]() 在
在 ![]() 上定义的 概率函数(probability function)或 概率测度(probability measure)、
上定义的 概率函数(probability function)或 概率测度(probability measure)、![]() 为事件A的 概率(probability)。
为事件A的 概率(probability)。
此时 ![]() 称作 概率空间(probability space)。
称作 概率空间(probability space)。
0x04 几何概率(geometric probability)
向某一可度量的区域内投一质点,如果所投的点落在门中任意区域 g 内的可能性大小与 g 的度量成正比,而与 g 的位置和形状无关,则称这个随机试验为几何型随机试验或几何概型,此处的度量就是测度,一维指长度,二维指面积,三维指体积等。
标本空间 ![]() 为非加算集合时,如果标准空间中的长度、面积和体积是有限的,被给予几何形测度
为非加算集合时,如果标准空间中的长度、面积和体积是有限的,被给予几何形测度 ![]() 时,事件A的概率定义如下:
时,事件A的概率定义如下:
此时 ![]() 满足概率函数的三大公理 (A1)(A2)(A3)。
满足概率函数的三大公理 (A1)(A2)(A3)。