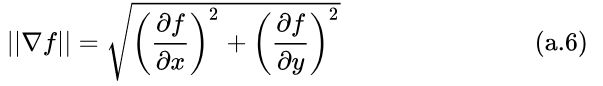Background Matting V2算法讲解
参考论文:Real-Time High-Resolution Background Matting,我也已经发布过Real-Time High-Resolution Background Matting的论文翻译。
BGM2算法内容的参考博客:人像抠图之Background Matting v2
附录一:深度学习的基础内容,没用深度学习基础的可以从附录一开始看。
1、问题定义
Background Matting v2(以下简称BGM2),一种实现人像抠图的算法,首先我们来看人像抠图的核心实现思想。
抠图算法的定义: I = α F + ( 1 − α ) B I = αF+(1-α)B I=αF+(1−α)B
已知输入图像 I I I,背景图像 B B B,求图像 I I I的前景 I I I,以及前景概率 α α α。(前景与背景相对,指我们所需的人像及人所持的物体)
上一代BGM1的方案是直接预测前景概率,或者再加上前景 ,通过这种方式合成的新图片会有比较明显的颜色溢出问题。如下图的眼镜内区域留下残留颜色。而使用前景残差作为预测目标,不仅可以加速收敛,还可以解决颜色溢出问题。
BGM2为了更好地解决在BGM1中存在的颜色溢出问题,定义了前景残差 F R = F − I F^{R} = F-I FR=F−I,而前景 F F F可以通过前景残差 F R F^R FR得到 (残差:在数理统计中是指实际观察值与估计值之间的差):
F = m a x ( m i n ( F R + I , 1 ) , 0 ) ( 1 ) F = max ( min ( F^R + I , 1 ) , 0 )\quad(1) F=max(min(FR+I,1),0)(1)

抠图问题是一个难易样本不均衡的问题,其中重要且难分的像素点往往只存在于前景的边缘,因为非边缘部分的像素点往往是纯粹的前景或者背景,因此值往往非 0 即 1 。而边缘部分的像素点不仅数量少,而且往往是一个介于 0 和 1 之间的浮点值,它的准确率的高低往往才最能反映抠图算法的精细度。
(题外话:本次服创比赛的要求的输出是,人像为白色,背景为黑色的二值图)

BGM2模型为了处理这个问题,提出了Base网络与Refine网络组成的结构。其中基础网络Base,用于快速的在降采样的图像上得到一个低分辨率的结果,微调网络Refine,是在Base网络的基础上,在高分辨下对选定的Patch进行进一步优化。如下图:

2、网络结构
我们先讨论算法模块的实现,然后再搭建网络模型。
BGM2的网络模型如下图:

图3:BGMv2的网络结构,其中蓝色的是 G b a s e G_{base} Gbase网络,绿色的是 G r e f i n e G_{refine} Grefine网络。
给定一张输入图像 I I I和背景图像 B B B,首先将其降采样 c c c倍,得到 I c I_c Ic和 B c B_c Bc。 G b a s e G_{base} Gbase取 I c I_c Ic和 B c B_c Bc作为输入,输出是降采样后同等尺寸的前景概率 α c α_c αc、前景残差 F c R F_c^R FcR、误差预测图 E c E_c Ec和一个32通道的隐藏特征 H c H_c Hc。
然后,细化网络 G r e f i n e G_{refine} Grefine利用 H c H_c Hc、 I I I和 B B B,只在预测误差 E c E_c Ec较大的区域,对 α c α _c αc 和 F c R F_c^R FcR进行细化,并在原始分辨率下产生α和前景残差 F R F^R FR。
2.1 Base网络
BGMv2的网络结构,由骨干网络,空洞空间金字塔池化和解码器三部分组成:
骨干网络:可以采用主流的卷积网络作为,作者开源的模型包括ResNet-50,ResNet-101以及MobileNetV2,用户可以根据速度和精度的不同需求选择不同的模型;
空洞空间金字塔池化:(Atrous Spatial Pyramid Pooling,ASPP)是由DeeplabV3提出并在实例分割领域得到广泛应用的结构,人像抠图和实例分割本质上式非常接近的,因此也可以通过ASPP来提升模型准确率;
解码器:解码器是由一些列的双线性插值上采样和跳跃连接组成,每个卷积块由3×3的卷积,Batch Normalization以及ReLU激活函数组成。
如上文所说, G b a s e G_{base} Gbase的输入是 I c I_c Ic和 B c B_c Bc,输出是 α c α_c αc、 F c R F_c^R FcR、 E c E_c Ec和 H c H_c Hc。其中的误差预测图Error Map E c E_c Ec的Ground Truth是 E ∗ = ∣ α − α ∗ ∣ E^∗=|α−α^∗| E∗=∣α−α∗∣,Error Map是一张人像轮廓图,通过对Error Map的优化,可以使得BGMv2有更好的边缘检测效果。

2.2 Refine网络
G r e f i n e G_{refine} Grefine的输入是在根据误差预测图 E c E_c Ec提取的 k 个补丁快(patches)上进行精校,k 可以提前指定选择 top-k 个或者根据阈值筛选得到若干个(用户也可以根据速度和精度的平衡自行设置 k 或者阈值的具体值。对于缩放到原图的 1 c \frac{1}{c} c1的 E c E_c Ec,我们首先将其上采样到原图的 1 4 \frac{1}{4} 41,那么 E 4 E_4 E4中的一个点就相当于原图上一个4×4的块,那么相当于我们要优化的像素点的个数共有16k个。

G r e f i n e G_{refine} Grefine 的网络分成两个阶段:在 1 2 \frac{1}{2} 21的分辨率和原尺寸的分辨率上,分别进行精校。
- Stage 1:首先将 G b a s e G_{base} Gbase的输出上采样到原图的 1 2 \frac{1}{2} 21,然后再根据 E 4 E_4 E4选择出的补丁块,从其周围裁剪出8×8的块,并分别通过两层3×3的有效卷积(valid padding)、Batch Normalization和ReLU,将块的尺寸依次降低为6×6、4×4。
- Stage 2:将Stage 1得到的4×4的Feature Map上采样到8×8,再依次经过两组3×3的有效卷积、Batch Normalization和ReLU,将Feature Map的最终尺寸降低到4×4。而这个Feature Map对应的ground truth就是我们上面根据 E 4 E_4 E4得到的补丁块。
最后我们将降采样的 α c α_c αc、 F c R F_c^R FcR再上采样到原图大小,再将Refine优化后的补丁块替换到原图中,便得到了最终的结果。
3、训练
3.1 损失函数
根据上面介绍的输入输出,我们可以把Base网络抽象为 G base ( I c , B c ) = ( α c , F c R , E c , H c ) G_{\text {base }}\left(I_{c}, B_{c}\right)= \left(\alpha_{c}, F_{c}^{R}, E_{c}, H_{c}\right) Gbase (Ic,Bc)=(αc,FcR,Ec,Hc),它的损失函数是由 α c , F c R , E c \alpha_{c}, F_{c}^{R}, E_{c} αc,FcR,Ec三部分组成,损失函数表示为式(2):
L base = L α c + L F c + L E c ( 2 ) \mathcal{L}_{\text{base}}=\mathcal{L}_{\alpha_{c}}+\mathcal{L}_{F_{c}}+\mathcal{L}_{E_{c}} \quad (2) Lbase=Lαc+LFc+LEc(2)
Refine网络可以抽象为 G refine ( α c , F c R , E c , H c , I , B ) = ( α , F R ) {G_{{\text{refine }}}}\left( {{\alpha _c},F_c^R,{E_c},{H_c},I,B} \right)=(\alpha ,{F^R}) Grefine (αc,FcR,Ec,Hc,I,B)=(α,FR),它的损失函数由α和 F R F^R FR组成,表示为式(3):
L refine = L α + L F ( 5 ) \mathcal{L}_{\text {refine }}=\mathcal{L}_{\alpha}+\mathcal{L}_{F} \quad (5) Lrefine =Lα+LF(5)
其中 L α \mathcal{L}_{\alpha} Lα是由前景概率α计算得到的特征向量,它包含α本身的L1损失和α的Sobel梯度 ∇ α ∇α ∇α的L1损失,如式(4):
L α = ∥ α − α ∗ ∥ 1 + ∥ ∇ α − ∇ α ∗ ∥ 1 ( 4 ) L_α=∥α−α^∗∥_1+∥∇α−∇α^∗∥_1 \quad (4) Lα=∥α−α∗∥1+∥∇α−∇α∗∥1(4)
其中 α ∗ α^∗ α∗为α的Ground Truth。图像梯度是指,图像强度或者颜色的方向变化率,能够更好的衡量图像边缘的清晰度,关于图像梯度的计算方法见附录2。
损失函数的第二项 L F \mathcal{L}_{F} LF计算的是前景损失,它先使用式(1)由 F R F^R FR得到 F F F,然后再在 α ∗ > 0 α^∗ >0 α∗>0的地方计算L1损失,表示为式(5):
L F = ∥ ( α ∗ > 0 ) ∗ ( F − F ∗ ) ) ∥ 1 ( 5 ) \left.\mathcal{L}_{F}=\|\left(\alpha^{*}>0\right) *\left(F-F^{*}\right)\right) \|_{1} \quad (5) LF=∥(α∗>0)∗(F−F∗))∥1(5)
其中 ( α ∗ > 0 ) (α^∗ > 0) (α∗>0)是一个布尔表达式。
L b a s e \mathcal{L}_{base} Lbase的第三项是关于Error Map的L2损失,它的作用是鼓励放大 α α α和 α ∗ α^∗ α∗直接的差值,表示为式(6):
L E = ∥ E − E ∗ ∥ 2 ( 3 ) \mathcal{L}_{E}=\left\|E-E^{*}\right\|_{2} \quad (3) LE=∥E−E∗∥2(3)
3.2 训练方式
由于文章包含多个模型和多个不同特征的数据集,因此我们这里介绍一下它的训练步骤:
- 先在VideoMatte240K数据集单独训练 G b a s e G_{base} Gbase ,再联合训练 G b a s e G_{base} Gbase 和 G r e f i n e G_{refine} Grefine ;
- 再使用PhotoMatte13K数据集联合训练两个模型以提高对模型在高分辨率图像上的表现效果;
- 最后在Distinctions-646上训练两个模型。
4、总结
BGM2性能的提升得益于重新设计的模型和采集的两个高分辨率的数据集。 G b a s e G_{base} Gbase 的结构参考了DeepLab v3,而 G r e f i n e G_{refine} Grefine则通过Error Map选取了一些难以处理的像素样本对其精校,提升了BGM2在细节上的表现力。
论文文献的附录
- B.网络架构和实现细节
- C.阐明了使用哪些关键字来抓取背景图像
- D.如何训练我们的模型,并展示了数据增强的细节
- E.展示了关于BGM2模型性能的额外指标
- F.用户研究中使用的所有定性结果,以及每个样本的平均得分
附录1:深度学习基础
放这里太长了,见深度学习理论基础
附录2:图像梯度的计算方法
一幅清晰的图像往往拥有强烈的灰度变化和层次感,而一幅模糊的图像则灰度变化不明显。而图像梯度往往就是用来衡量图像灰度的变化率的。图像可以看做二维离散函数,而图像梯度便是对这个二维离散函数的求导。
离散函数的求导往往使用差商的方式进行计算,例如中心差商,如式(a.1)所示。

在图像中, h=1 ,中心差商简化为式(a.2)。

上述操作对应的一维卷积核为[-1,0,1]。如果考虑到上下两行和当前行时(当前行拥有更高的权值),我们便可以得到一个Sobel卷积核,如式(a.3)。

上面的卷积核计算的是图像在x方向上的梯度。同理,我们也可以得到计算图像在y方向梯度的卷积核 S o b e l y Sobel_y Sobely,如式(a.4)。

那么图像在两个方向的梯度边,也可以通过两个卷积操作来完成,如式(a.5)。

图像的梯度向量为 ∇ f = [ ∂ f ∂ x , ∂ f ∂ y ] ∇f = [\frac{∂f}{∂x},\frac{∂f}{∂y}] ∇f=[∂x∂f,∂y∂f]。那么图像的梯度值则可以表示为式(a. 6).