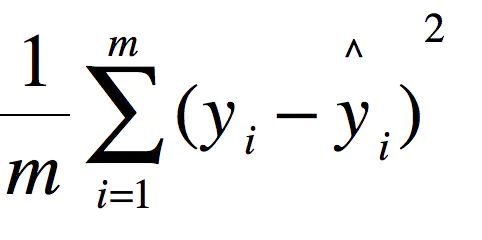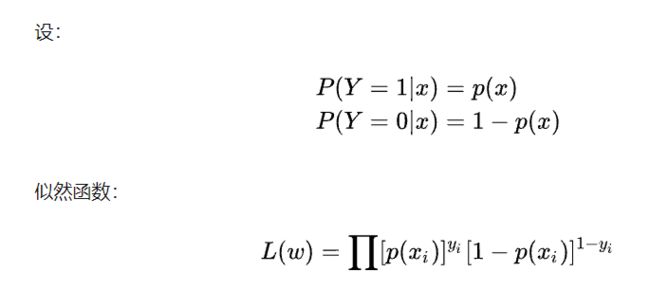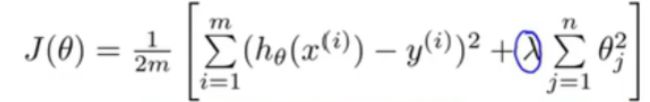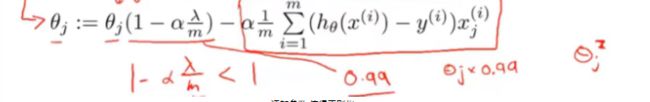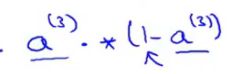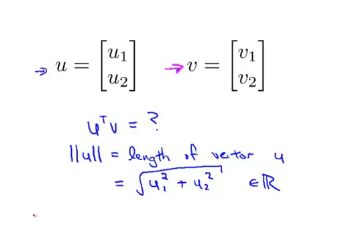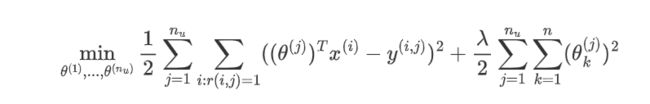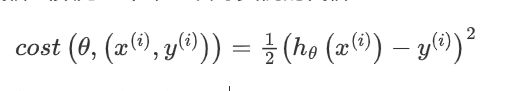机器学习_吴恩达-总

机器学习

个人总结：机器学习就是通过数据以及对应的算法让数据变得有规律可循，并应用于生活

1. 机器学习分类：有监督学习和无监督学习
2. 有监督学习：有辅助性的人为操作，帮助机器更好的算出目标值。如数据标注
3. 无监督学习：给一大堆数据，让机器自己去寻找当中的规律

_2021级_ 第7周_学习总结

21.10.18-21.10.24

周学习任务：

• 100% 回顾吴恩达机器学习前4章节

• 10% 神经网络学习

​

​

一、回顾机器学习前4章节

机器学习：用已知的数据集通过数学模型使得程序能够像人一样的去思考，然后对未知数据做出预测

1.机器学习分类：有监督学习 & 无监督学习

• 有监督学习：有明确的数据，有明确的答案。常用于分类问题以及回归问题。

• 无监督学习：不会告诉什么是错什么是对，只是被告知一堆数据，但是不知道干嘛，不知道类型，让机器自己找到答案。常用聚类算法。

  

2.线性回归模型&梯度下降

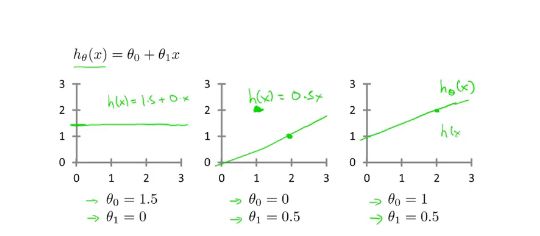
• 回归模型的一般示例：函数公式：$h{}_{\theta }(x)=\theta {}_0+\theta {}_{1}x$ 其中==$\theta {}_0$和$\theta {}_1$是整个函数中的变量，通过控制这两个变量调整函数的图像，使得输入参数和输出参数能够达到拟合，做出更正确的预测。一般可以使用for循环来进行两个参数的选择，但是计算出的值与真实值之间会存在误差，我们需要对误差进行获取以及得到最优的参数值，所以引入了代价函数==进行误差的分析。

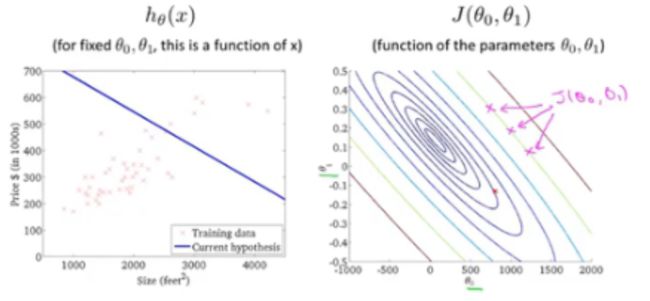
• 代价函数：在回归模型中，使用$J(\theta {}_0,\theta {}_1)=\frac{1}{2m}{\sum }_{i=1}^m\frac{(预测值h{}_{\theta }(x_i)-真实值y{}_i{)}^2}{样本数据数量m}$来作为其代价函数，如下通过$\theta {}_1$的变化，求得对应$\theta {}_1=1$时有最小的代价函数值。当对下图右边进行求导时$\frac{\partial J(\theta {}_1)}{\partial \theta {}_1}$，会发现越靠近最优解时，其偏导数是越靠近0的。

  

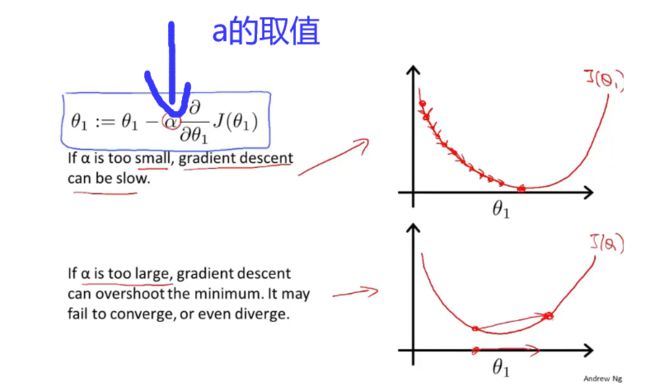
• 梯度下降：为了使得参数变化和代价函数关联起来，使用$\theta {}_j:=\theta {}_1-\alpha \frac{\partial J(\theta {}_0,\theta {}_1)}{\partial \theta {}_j}$对各个参数进行同步改值，其中==$\alpha$==为学习率，太大太小均不可。梯度下降的过程中，接近最优解的时候，偏导数会越来越接近0，那步长也就会越来越小，最终达到合适的权重值。一下为梯度下降算法的流程。

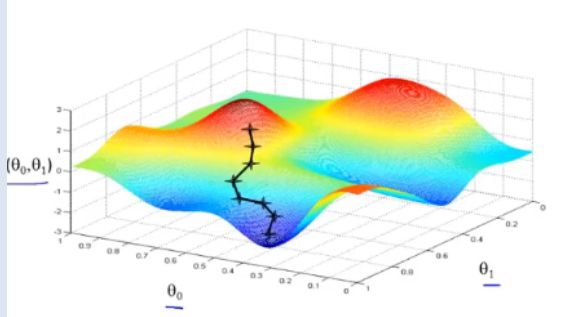
• 多个参数的梯度下降图像（等高线）

• 回归模型的批量参数梯度下降一般是要看着整个训练集进行下降。有全局最优解。

3.线性回归模型的实践-房价的预测

• 模型训练

from sklearn.linear_model import LinearRegression
from  sklearn.model_selection import train_test_split
from  sklearn.datasets import fetch_california_housing as fch #加州房价预测数据
#数据的提取
feature=fch().data
target=fch().target

#数据的拆分
x_train,x_text,y_train,_y_test=train_test_split(feature,target,test_size=0.1,random_state=2021)
linear=LinearRegression() #模型初始化
#模型的训练
linear.fit(x_train,y_train)

#得到权重参数值 linear.coef_   
#打印权重参数名以及参数值
[*zip(fch().feature_names,linear.coef_)]

可以看到值越小的参数对最后的预测值影响越小。

• 模型的评估：使用==MSE（均方误差）==来衡量真实值和预测值之间的差异，其实就是loss函数

• 回归模型的评价指标

  

  from sklearn.metrics import mean_squared_error 
  y_true=y_test #将真实值存到y_true中
  y_pred=linear.predict(x_test)  #通过模型对测试数据集中的数据进行预测
  
  mean_squared_error(y_true,y_pred)#MSE值0.5253224455144776
  
  #使用交叉验证中的均方误差
  from sklearn.model_selection import cross_val_score
  cross_val_score(linear,x_train,y_train,cv=5,scoring='neg_mean_squared_error').mean() 
  #loss（损失值）-0.5284704303001286正数就为MSE
  

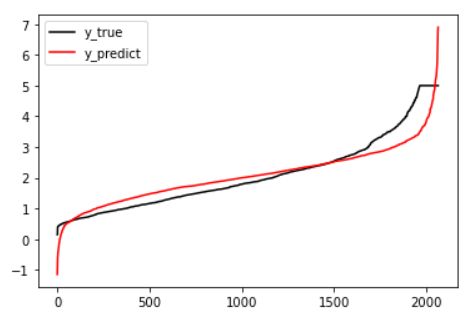
• 拟合图

  #绘制拟合图
  %matplotlib inline
  import matplotlib.pyplot as plt
  
  y_pred=linear.predict(x_test)
  
  plt.plot(range(len(y_test)),sorted(y_test),c="black",label="y_true")
  plt.plot(range(len(y_pred)),sorted(y_pred),c="red",label="y_predict")
  
  plt.legend()
  plt.show
  

  

  当mse越接近0的时候，数据将会更加的拟合

4.矩阵和向量

在使用线性回归梯度下降的时候，其中$\theta$的值是通过代价函数反复确定，增加了循环地次数，在矩阵的运算中，我们可以一次使用多组数据作为参数，求出多组不同的预测值。所以当函数方程存在多个输入参数时，方便求解。引入矩阵时为了后面的正规方程寻最优解

5.多元线性回归&梯度下降&正规方程

• 多元线性回归梯度下降
  • 函数：$h(x)={\theta }^{T}x=\theta {}_{0}x{}_0+\theta {}_{1}x{}_1+\theta {}_{2}x{}_2+...+\theta {}_{n}x{}_n$
  • 代价函数：$J(\theta {}_0,...,\theta {}_n)=\frac{1}{2m}{\sum }_{i=1}^m(h{}_{\theta }(x^i)-y^i{)}^2$
  • 梯度下降：KaTeX parse error: Undefined control sequence: \part at position 38: …-\alpha \frac {\̲p̲a̲r̲t̲ ̲J(\theta{_0},..…
  • 运行流程：对多个参数实行梯度下降，进而取到最优值

• 特征缩放：当数据很大的时候，为了方便计算，我们可以将简单的有规律的数值进行特征缩放，使得我们的梯度下降的更快，收敛也更快。

  • 数据有一定范围：可以将数据成范围比例缩小
  • 均值归一化：$\frac{x-average}{range}$

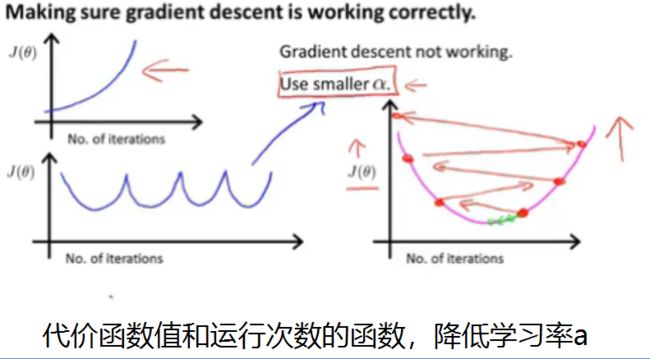
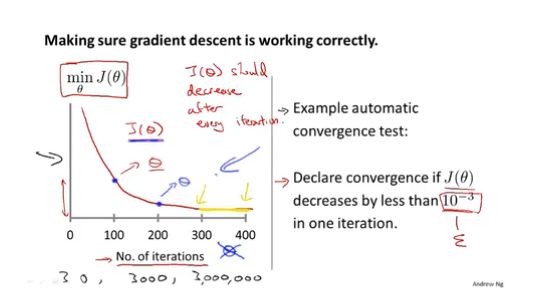
• 监控代价函数：为了监控是否达到最小，可以使用执行次数和代价函数值画出图像就行监控。一般可以使用一个阈值进行自动收敛测试。代价函数也有有很大部分收学习率的影响，所以我们也要通过合适的算法选取合适的学习率

• 正规方程

  • 梯度下降核心：通过对代价函数求偏导，得到近似0的值（等于0就是类似于极值的求解），最终得到合适的参数

  • 正规方程核心：利用矩阵的运算：$\theta X=Y $通过矩阵的变换（转置，逆矩阵等）得到$\theta$的值

    

  • 求得$\theta =(X^{T}X{)}^{-1}{X}^{T}Y$ （考虑是否可逆：一般均可在octave中用pinv算出，inv只能算不可逆的）

  • 不可逆的情况：特征值之间有关系比例

  • 奇异矩阵或者退化矩阵：存在多余的feature

6.正规方程VS梯度下降

二、神经网络学习

让程序像大脑一样思考，模拟大脑的神经传递，将参数通过一层一层的映射关系传递到最后得到最终的结果

1.现实问题

当某一个模型中输入参数变得很大的时候，如图像中的像素块分解作为参数，使用常规的模型会使得计算量变得很大。

2.神经网络

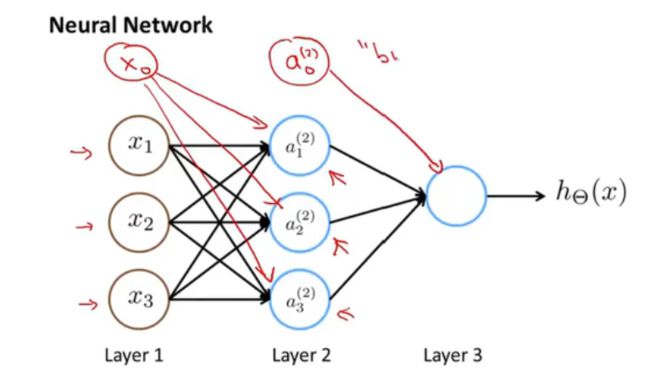
• 第一次的参数输入后，将通过函数算出第二层的目标值。第二层的目标值又作为第三层的参数输入。以此类推
• $a{{}_1}^{(2)}=g(\theta {{}_1{}_0}^{(1)}x{}_1+\theta {{}_1{}_1}^{(1)}x{}_2+\theta {{}_1{}_2}^{(1)}x{}_3)$ 表示第2层的a1是第一层通过函数进行变换得到的，参数为第一层对应的权重。
• 简单的模拟：不同的颜色有不同的映射规则，求得的每一个参数也不一样

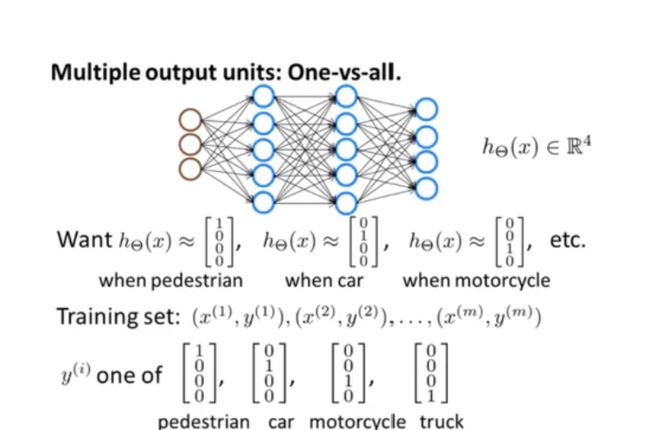
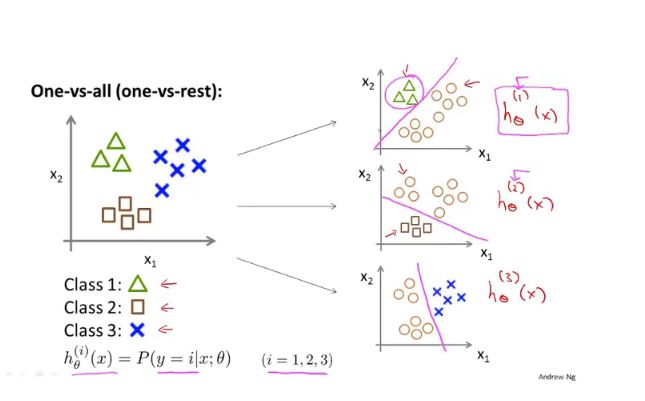
3.多元分类

存在一组数据有海量数据，我们需要将这里面的数据进行多个分类，其最终的预测值不止一个。

_2021级_ 第8周_学习总结

21.10.25-21.10.31

周学习任务：

• 100% 回顾吴恩达机器学习：分类算法

• 80% 神经网络学习

​

一、回顾机器学习

机器学习：用已知的数据集通过数学模型使得程序能够像人一样的去思考，然后对未知数据做出预测

1.机器学习分类：有监督学习 & 无监督学习

• 有监督学习：有明确的数据，有明确的答案。常用于分类问题以及回归问题。

• 无监督学习：不会告诉什么是错什么是对，只是被告知一堆数据，但是不知道干嘛，不知道类型，让机器自己找到答案。常用聚类算法。

  

2.逻辑回归模型

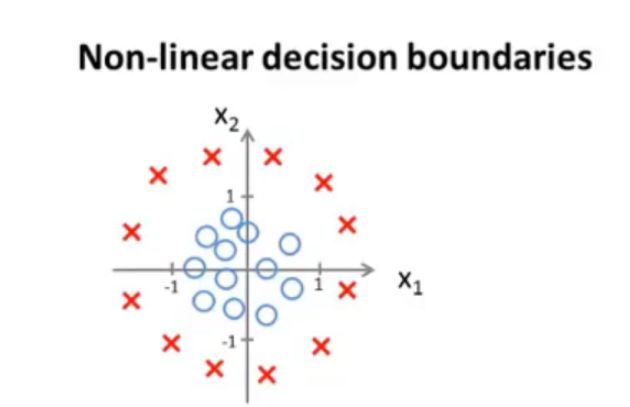
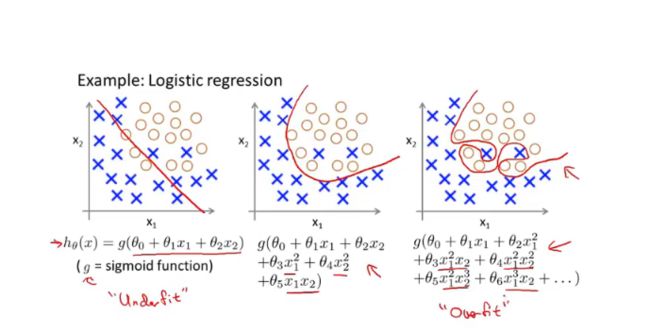
• Logistic 回归主要用于分类问题，下面是简单二分类，对于所给数据集假设存在这样的一条直线可以将数据完成线性可分。

• 较复杂的分类：通过不断地添加高项式使得分类趋向正确，但是会存在过拟合的现象。

• 对于已知的输入参数，其最后的结果只有0,1。其逻辑回归的函数为对数几率函数：==$h{}_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$==和linear一样需要选取合适的参数达到更好的拟合。通过代换得${\theta }^{T}x=\ln \frac{y}{1-y}$ =》${\theta }^{T}x=-\ln (1-y)+\ln (y)$ 可以得出
  • ${\theta }^{T}x$的值越趋向无穷的时候$P(Y=1|x)$ 越接近1,
  • y从0->1的时候，x趋向$\infty$（无穷）
• 使用线性回归模型的预测值逼近分类任务真实标记的对数几率，其优点有：
  • 直接对分类的概率建模，无需实现假设数据分布，从而避免了假设分布不准确带来的问题（区别于生成式模型）；
  • 不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务很有用；
  • 对数几率函数是任意阶可导的凸函数，有许多数值优化算法都可以求出最优解。

• 代价函数：在逻辑回归模型中常常使用极大似然法求解，即找到一组参数，使得在这组参数下，我们的数据的==似然度（概率）==最大

衡量模型预测错误的程度，我们取整个数据集上的平均对数似然损失，我们可以得到代价函数为：

即

$J(\theta )=-\frac{1}{m}[{\sum }_{i=1}^m{y}^{(i)}\ln h_{\theta }(x^{(i)})+(1-y^{(i)})\ln (1-h_{\theta }(x^{(i)}))]$

= $-\frac{1}{m}[{\sum }_{i=1}^m{y}^{(i)}({\theta }^{T}x)-\ln (1+e^{{\theta }^{T}x})]$

• 在逻辑回归模型中，最大化似然函数和最小化损失函数实际上是等价的。

• 梯度下降：为了使得参数变化和代价函数关联起来，使用$\theta {}_j:=\theta {}_j-\alpha \frac{\partial J(\theta )}{\partial \theta {}_j}$对各个参数进行同步改值，其中==$\alpha$==为学习率，太大太小均不可。梯度下降的过程中，接近最优解的时候，偏导数会越来越接近0，那步长也就会越来越小，最终达到合适的权重值。一下为梯度下降算法的流程。

对代价函数求偏导得到：KaTeX parse error: Undefined control sequence: \part at position 8: \frac {\̲p̲a̲r̲t̲ ̲J(\theta)}{\par…

• 高级优化算法

  

• 多元分类思想：多次切割。

  

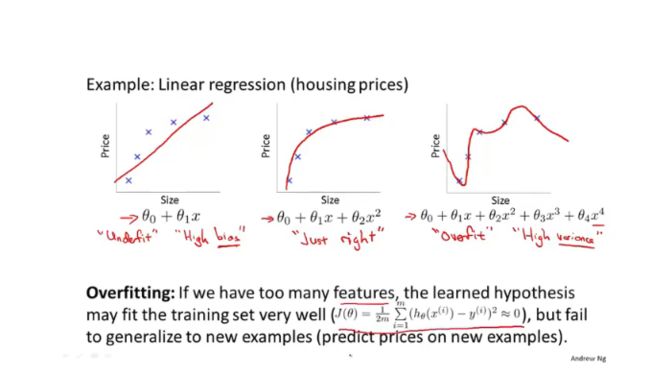
3.过拟合欠拟合

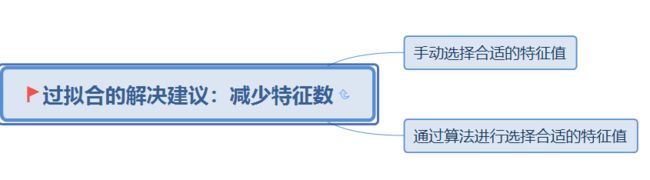
• 参数进行缩放。

4. 正则化-----可以解决过拟合的问题

正则化是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合.

在经验风险最小化的基础上（也就是训练误差最小化），尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单

正则化一般会采用 L1 范式或者 L2 范式

• L1 正则化：LASSO 回归，相当于为模型添加了这样一个先验知识：权重服从零均值拉普拉斯分布。
• 
• L2 正则化：Ridge 回归，相当于为模型添加了这样一个先验知识：w 服从零均值正态分布。
• 

​

• 线性回归的正则化:在原有的基础LOSS公式上加上一个 变化的值

​ 类似于正规方程中加入某一矩阵：

• 逻辑回归的正则化

  

• 

  

• L1 正则化就是在 loss function 后边所加正则项为 L1 范数，加上 L1 范数容易得到稀疏解（0 比较多）。

• L2 正则化就是 loss function 后边所加正则项为 L2 范数的平方，加上 L2 正则相比于 L1 正则来说，得到的解比较平滑（不是稀疏），但是同样能够保证解中接近于 0（但不是等于 0，所以相对平滑）的维度比较多，降低模型的复杂度。

二、神经网络学习

让程序像大脑一样思考，模拟大脑的神经传递，将参数通过一层一层的映射关系传递到最后得到最终的结果

1.逻辑线性回归的代价函数和神经网络

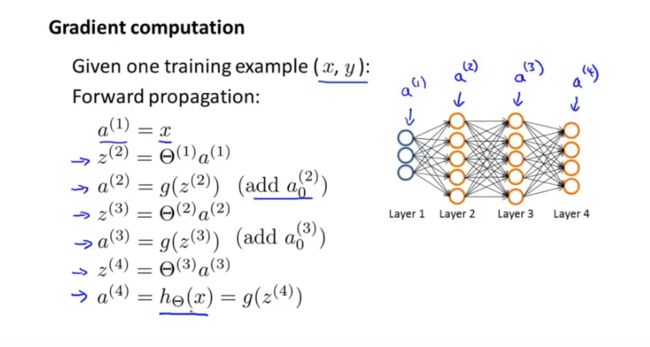
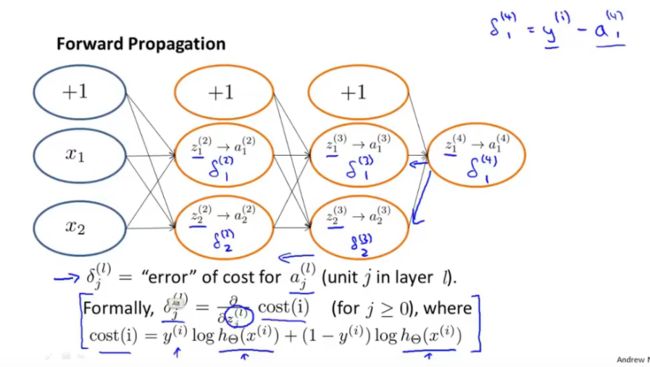
2.前向传播

前一个参数计算出值后作为后一个公式的参数值

$a_j^{(l)}$表示第$l$层的$j$个结点的激活值，这个值通过激活函数==sigmod（z）==计算得到。

$z_1^2={\theta }_0+{\theta }_1{x}_1^1+{\theta }_2{x}_2^1$ 第二层的z由第一层权重和 $z$通过激活函数sigmod得$a^2$ 。 下图为计算$z^3$的图像。

3.使用反向传播最小化神经网络

${\delta }_j^{(l)}$代表了第$l$层的$j$个结点的误差${\delta }_j^{(l)}=a_j^l-y_j$ (激活项的误差)。同时也可以写成向量的形式：${\delta }^l=a^{(l)}-y$

上图公式含义：第三层的误差==${\delta }^3$== 是第三层参数==$\theta$==的转置乘以 第四层的误差项向量 点乘 激活函数g在输入值为$z^3$时所求的导数最后的值为如下图所示，同时误差层数不能算到第一层因为是输入层，没有意义。

实际上得到某一层的代价函数的偏导就等于 该层激活项乘以下一层的误差值。

• 假设输出项只有一项同时忽略正则化，提取出cost函数作为衡量预测值的准确度：

上图中得到其误差为cost对z的偏导，其含义：衡量的是为了影响这些中间值，我们改变神经网络中的权重的程度，进而影响输出函数h(x),并影响所有的代价函数

计算${\delta }_2^{(2)}={\theta }_{12}^{(2)}{\delta }_1^{(3)}+{\theta }_{22}^{(2)}{\delta }_2^{(3)}$ 其中 ${\delta }_2^{(3)}={\theta }_{12}^{(3)}{\delta }_1^{(4)}$

4.梯度检测

取消了直接利用求导的法则去运算，而使用微分的概念去近似求值来对神经网络最后的模型进行梯度检测，确认梯度下降是正确的。在执行梯度下降的时候不要执行检测算法，因为检测算法的运算时间很慢。

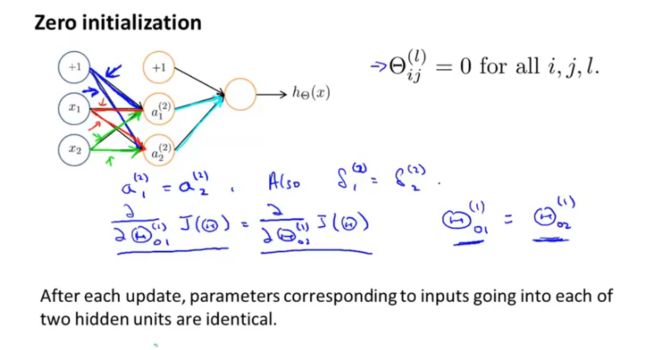
5.随机初始化

在使用梯度下降等算法的时候，我们需要对$\theta$ 的值进行初始化，然后再进行梯度下降，所以就要选择合适的初始化值。

• 对称权重：均初始化为0时的情况：

• 随机权重：

6.总结

• 通常情况下：隐藏单元越多越多；输入参数数量因该和隐藏单元一致或者 隐藏单元是输入参数的n倍。
• 输出项存在多个分类的时候，将y写成对应的向量值。
• 神经网络一般的执行流程
  • 1：初始化随机权重
  • 2 : 实现前向传播，输入 $x并可通过函数$$h_{\theta }(x)$ 得到结果
  • 3：实现代价函数 $J(\theta )$
  • 4：反向传播计算代价函数的偏导数(循环)
  • 5: 使用梯度检测进行检测是否正确
  • 6：执行梯度下降函数

三、模型的选择和一些操作方法

1.数据集的处理

可以将数据集拆分成30%-70%比例，或者详细分为：训练集，交叉集，验证集。

2.模型的选择上

使用交叉集cv误差来选择模型。使用train训练模型，通过梯度下降之后，得到较好的参数；再使用cv数据集将这个参数代入，求出cv误差。

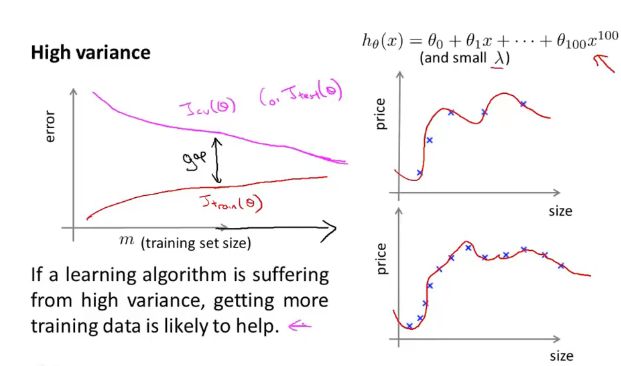
3.算法的偏差和方差导致过拟合问题

图像：多项式的次数和训练误差的图像，以及交叉误差的函数图像。

• 高方差的情况：训练集的误差很低，相当于过拟合，导致了交叉数据集中的误差很高。

4.使用正则化解决过拟合的问题（神经网络同）

在使用正则化的过程中，我们需要考虑 $\lambda$ 的取值；通过一点一点的变化使得交叉集的误差最低。

• 正则化后的函数对比：当参数$\lambda$ 很小的时候，会发生过拟合现象，所以训练集的误差会很小，但是交叉验证的误差会很大；当参数很大的时候，会出现欠拟合现象，训练集的误差会变得很大，同时交叉验证的误差也会变大。所以引入了正则化参数与loss学习曲线
• 

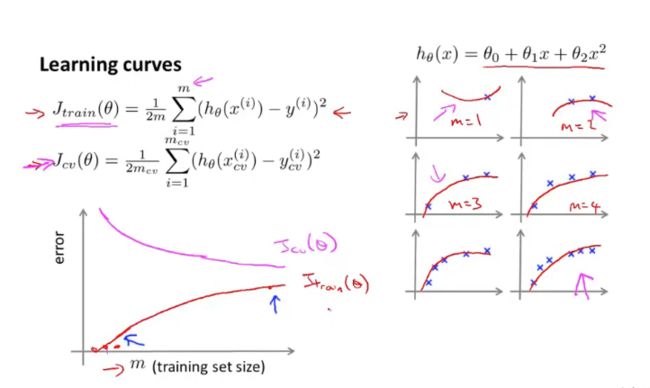
5.学习曲线

学习曲线只要是检查我们的算法是否正常，是出于偏差还是方差

案例：参数越多的时候，交叉验证会越好，但是训练集的误差会变大

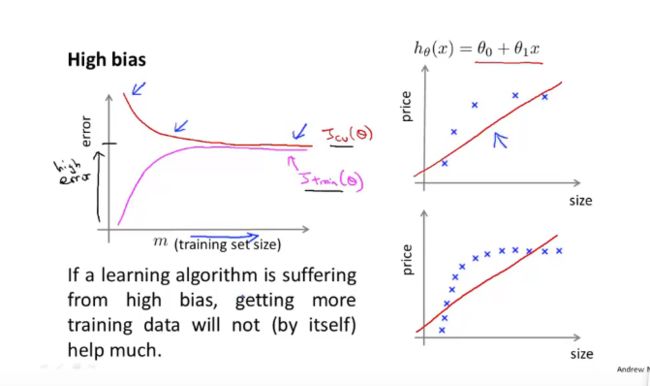
• 高偏差：随着我们增加m，交叉误差不会减少，同时交叉误差和训练误差间距很小；导致算法无错误，结果无意义。

• 高方差：训练误差和交叉误差之间的间距很大，当参数越多的时候，会改善这个情况。随着参数个数的增加交叉验证的误差远大于训练集（下降）的误差。

四、模型的度量方法–并不是准确率高就是好的模型

1.评估度量值：查准率（Precesion）和召回率recall（查全率）

• 瞎猜的概率：$\frac{FP+TN}{总的和}$

2.P/R的自动权衡

• $F_{1}Score$

一元线性回归的简单模拟代码。

import numpy as np
import matplotlib.pyplot as plt

#数据的载入
data=np.genfromtxt("data.csv",delimiter=",")
x_data=data[:,0] #数据的切分
y_data=data[:,1]
plt.scatter(x_data,y_data)#数据的散点图
plt.show()


#学习率
lr=0.0001
#截距
b=0
#斜率
k=0
#最大的迭代次数
epochs=50

#最小二乘法  求代价函数
def compute_error(b,k,x_data,y_data):
    totalError=0
    for i in range(0,len(x_data)):
        totalError+=(y_data[i]-(k*x_data[i]+b))**2
    return totalError/float(len(x_data))/2.0

#梯度下降算法
def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
    #计算总的数据量
    m=float(len(x_data))
    #循环
    for i in range(epochs):
        b_grad=0
        k_grad=0
        #计算梯度的总和再求平均
        for j in range(0,len(x_data)):
            #对theta0求导
            b_grad+=-(1/m)*(y_data[j]-(k*x_data[j]+b))
            #对theta1求导
            k_grad+=-(1/m)*x_data[j]*(y_data[j]-(k*x_data[j]+b))
        b-=(lr*b_grad)
        #参数-学习率*偏导数
        k -= (lr*k_grad)
        #每一次迭代求出参数1和2的值
        #每5次打印对应的图像
#         if i%5==0:
#             print("epochs:",i)
#             plt.plot(x_data,y_data,'b.')
#             plt.plot(x_data,k*x_data+b,'r')
#             plt.show()
    return b,k
print("Starting b={0},k={1},error={2}".format(b,k,compute_error(b,k,x_data,y_data)))


print("running...")
b,k=gradient_descent_runner(x_data,y_data,b,k,lr,epochs)
print("After{0} iterations b={1},k={2},error={3}".format(epochs,b,k,compute_error(b,k,x_data,y_data)))

#画图
plt.plot(x_data,y_data,'b.')
plt.plot(x_data,k*x_data+b,'r')
plt.show(

_2021级_ 第9周_学习总结

21.11.1-21.11.6

周学习任务：

• 90% SVM

​

一、SVM（支持向量机）

支持向量机是在二分类的问题中找到一个最有把握把两类样本分开的一个超平面(最优超平面)， 既然是最优问题，就需要先把找最优超平面的问题用数学的方式表示出来，得到了原始的优化目标(SVM原始问题)，但是该原始问题对于参数会有约束，不太好求出最优超平面，于是转成无约束问题，并借助凸优化的相关理论把其转成等价的对偶问题，最后通过求对偶问题的解得到最终的超平面。

SVM优缺点:

• 优点：

  • 严格的数学理论支持， 可解释强。
  • 能找出对任务至关重要的样本(支持向量)。
  • 由于SVM是一个凸优化问题，所以求得的解一定是全局最优而不是局部最优。
  • 不仅适用于线性线性问题还适用于非线性问题(用核技巧)。
  • 拥有高维样本空间的数据也能用SVM，这是因为 SVM 对偶形式求解的复杂度与样本数量而不是维数相关，因此 SVM 很擅长解决高维稀疏的问题。

• 缺点：

  • 二次规划问题求解将涉及m mm阶矩阵的计算(m mm为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)。
  • 模型预测时，预测时间与支持向量的个数成正比。当支持向量的数量较大时，预测计算复杂度较高。因此支持向量机目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务。
  • 当样本数量比较大时，效果通常不如神经网络。

吴达恩视频中SVM：

当训练集Y=1的时候，要想上面的值为0，则cost1=0的时候，z>=1

当训练集Y=0的时候，要想上面的值为0，则cost0=0的时候，z<=-1

• 1和-1就是一个安全距离，决策边界

当C很大的时候：使得内部值为0

下面的案例是多个直线划分正负样本，存在蓝色线的margin，叫SVM的间距，具有鲁棒性（越大越好），最大分类器

当c非常大的时候，会将黑线变成紫线，但是紫线的情况非常不好，C的作用类似于KaTeX parse error: Undefined control sequence: \y at position 2: 1\̲y̲ ,C不是很大的时候，可能会得到黑线

大间隔分类器的理解

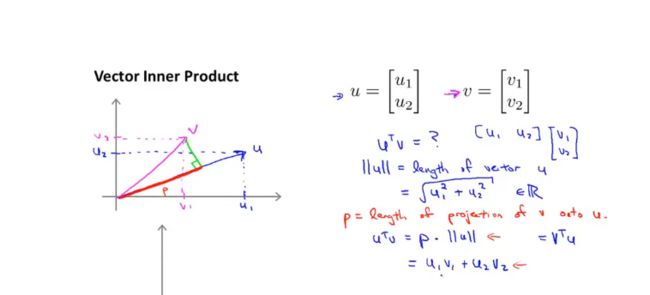
回顾向量内积：根据毕达哥拉斯定理会得到向量积

两个向量的乘积： V*U的乘积，实际上是P在V在U上的投影乘以u的范数。V*U=P*||u||

u是一个向量，可以理解为参数的向量（x为${\theta }_1$，y轴为${\theta }_2$）,V向量位置可以理解为样本的位置，样本对u向量做投影，会存在为正为负的情况，就是正样本和负样本，其划分线是u的垂线。

向量的范数：

${\theta }_0$为0的时候，从原点出发，x的位置在$\theta$的投影就是$p^i$ 然后其${\theta }^T{X}^i=p^i||\theta ||$ 值大于1 正样本。类似于$|x|\ast |\theta |\ast cos夹角$。

上图具体是指训练样本x在theta上的投影。

向量参数实际上是和$\theta$成正交的。

svm原理：

• 支持向量机的目标函数就是努力寻找最大边界，也称为大间距分类器，这个最大边界即是样本在$\theta$上的投影。要增大边界，就是想办法增大他们的投影，最后取出较小的$\theta$值。

核函数

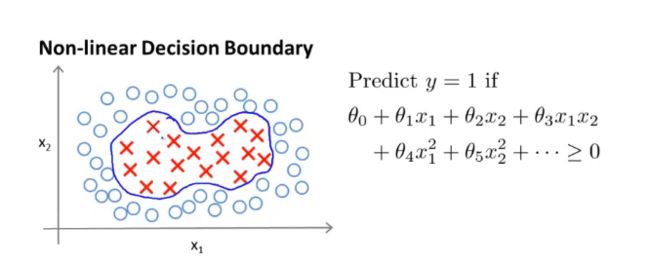
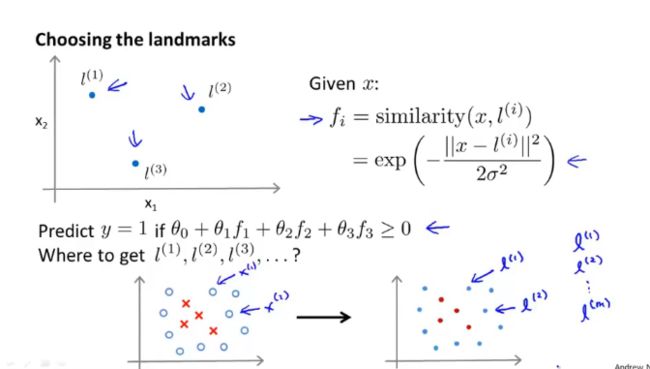
• 构造复杂的多项式可以画出这个图像，但是很多高阶函数我们并不知道是否适用，同时高阶太多会导致计算量增大，而核函数是一个更加有效的解决办法

这里案例是高斯核函数，相似函数，x与标记点之间的位置越近越为1，反之

当标记的值为3.5时，当分母为1时，f的高度约为1。

• 标记点的选择：将所有的样本点设置为标记点

• 算出所有的x与其他标记点之间的位置距离，也可以是相似度

_2021级_ 第10周_学习总结

21.11.8-21.11.14

一、无监督学习

在原有的监督学习中，无监督学习和监督学习相比监督学习有标签信息，但是无监督学习是没有标签信息的，我们需要使用特有的函数方法使数据集寻找数据中间的内在关系，如将上图分为两个点集（簇）的算法被称为聚类算法。

K-means均值算法

• 算法接收没有标记的数据集，然后将数据聚类成不同的组。
• 是一个迭代算法，使用该算法的一般步骤为：

1. 确定需要分的类数量n
2. 选择K个随机的点，称为***聚类中心*** **cluster centroids**
3. 于数据集中的每一个数据，按照距离$K$个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类
4. 计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置。
5. 重复上面步骤，到中心点不在变化

实例：

迭代一次

迭代3次

迭代10次

K-均值的代价函数-畸变函数

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，其中${\mu }_{c^{(i)}}$代表与$x^{(i)}$最近的聚类中心点，要找使得代价函数最小的 $c^{(1)}$,$c^{(2)}$,…,$c^{(m)}$和${\mu }^1$,${\mu }^2$,…,${\mu }^k$：

$$J(c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_K)=\frac{1}{m}\sum _{i=1}^m{\Vert X^{\left(i\right)}-{\mu }_{c^{(i)}}\Vert }^2$$

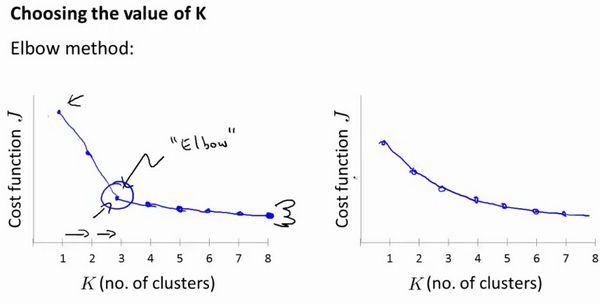
• 聚类数量的选择可以通过代价函数和K的图像来选择（拐点处-肘部法则）

聚类的相关资料-距离计算方法

1.相似度/距离计算方法总结

(1). 闵可夫斯基距离Minkowski/（其中欧式距离：$p=2$)

$dist(X,Y)={\left({\sum _{i=1}^n\left|x_i-y_i\right|}^p\right)}^{\frac{1}{p}}$

(2). 杰卡德相似系数(Jaccard)：

$J(A,B)=\frac{|A\cap B|}{|A\cup B|}$

(3). 余弦相似度(cosine similarity)：

$n$维向量$x$和$y$的夹角记做$\theta$，根据余弦定理，其余弦值为：

$cos(\theta )=\frac{x^{T}y}{|x|\cdot |y|}=\frac{\sum _{i=1}^n{x}_i{y}_i}{\sqrt{\sum _{i=1}^n{x_i}^2}\sqrt{\sum _{i=1}^n{y_i}^2}}$
(4). Pearson皮尔逊相关系数：
${\rho }_{XY}=\frac{\mathrm{cov}(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{E[(X-{\mu }_X)(Y-{\mu }_Y)]}{{\sigma }_X{\sigma }_Y}=\frac{\sum _{i=1}^n(x-{\mu }_X)(y-{\mu }_Y)}{\sqrt{\sum _{i=1}^n{(x-{\mu }_X)}^2}\sqrt{\sum _{i=1}^n{(y-{\mu }_Y)}^2}}$

Pearson相关系数即将$x$、$y$坐标向量各自平移到原点后的夹角余弦。

2.聚类的衡量指标

(1). 均一性：$p$

类似于精确率，一个簇中只包含一个类别的样本，则满足均一性。其实也可以认为就是正确率(每个 聚簇中正确分类的样本数占该聚簇总样本数的比例和)

(2). 完整性：$r$

类似于召回率，同类别样本被归类到相同簇中，则满足完整性;每个聚簇中正确分类的样本数占该类型的总样本数比例的和

(3). V-measure:

均一性和完整性的加权平均

$V=\frac{(1+{\beta }^2)\ast pr}{{\beta }^2\ast p+r}$

(4). 轮廓系数

样本$i$的轮廓系数：$s(i)$

簇内不相似度:计算样本$i$到同簇其它样本的平均距离为$a(i)$，应尽可能小。

簇间不相似度:计算样本$i$到其它簇$C_j$的所有样本的平均距离$b_{ij}$，应尽可能大。

轮廓系数：$s(i)$值越接近1表示样本$i$聚类越合理，越接近-1，表示样本$i$应该分类到 另外的簇中，近似为0，表示样本$i$应该在边界上;所有样本的$s(i)$的均值被成为聚类结果的轮廓系数。

$s(i)=\frac{b(i)-a(i)}{max\{a(i),b(i)\}}$

(5). ARI

数据集$S$共有$N$个元素， 两个聚类结果分别是：

$X=\{X_1,X_2,...,X_r\},Y=\{Y_1,Y_2,...,Y_s\}$

$X$和$Y$的元素个数为：

$a=\{a_1,a_2,...,a_r\},b=\{b_1,b_2,...,b_s\}$

记：$n_{ij}=\left|X_i\cap Y_i\right|$

$ARI=\frac{\sum _{i,j}{C}_{n_{ij}}^2-\left[\left(\sum _i{C}_{a_i}^2\right)\cdot \left(\sum _i{C}_{b_i}^2\right)\right]/C_n^2}{\frac{1}{2}\left[\left(\sum _i{C}_{a_i}^2\right)+\left(\sum _i{C}_{b_i}^2\right)\right]-\left[\left(\sum _i{C}_{a_i}^2\right)\cdot \left(\sum _i{C}_{b_i}^2\right)\right]/C_n^2}$

二、数据压缩

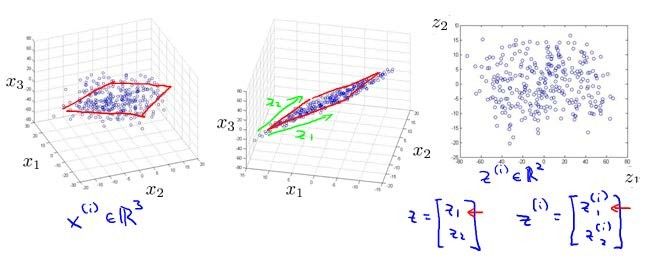
• 将数据从三维降至二维：将三维向量投射到一个二维的平面上，强迫使得所有的数据都在同一个平面上，降至二维的特征向量。

• 主成分分析(PCA)是最常见的降维算法：

在PCA中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据都投射到该向量上时，我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量，而投射误差是从特征向量向该方向向量作垂线的长读。将$n$维数据降至$k$维，目标是找到向量$u^{(1)}$,$u^{(2)}$,…,$u^{(k)}$使得总的投射误差最小

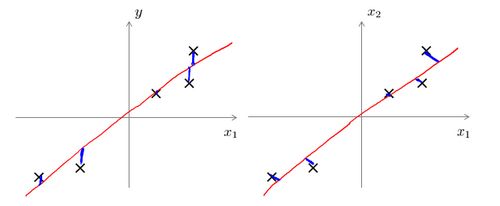
主成分分析与线性回归是两种不同的算法。主成分分析最小化的是投射误差（Projected Error），而线性回归尝试的是最小化预测误差。线性回归的目的是预测结果，而主成分分析不作任何预测。上图中，左边的是线性回归的误差（垂直于横轴投影），右边则是主要成分分析的误差（垂直于红线投影）。

PCA 减少$n$维到$k$维算法：

第一步是均值归一化。我们需要计算出所有特征的均值，然后令$x_j=x_j-{\mu }_j$如果特征是在不同的数量级上，我们还需要将其除以标准差 ${\sigma }^2$。

第二步是计算协方差矩阵（covariance matrix）$\Sigma$：
$\sum =\frac{1}{m}{\sum }_{i=1}^n\left(x^{(i)}\right){\left(x^{(i)}\right)}^T$，$$Sigma=\frac{1}{m}\sum _{i=1}^n\left(x^{(i)}\right){\left(x^{(i)}\right)}^T$$

第三步是计算协方差矩阵$\Sigma$的特征向量（eigenvectors）:

对于一个 $n\times n$维度的矩阵，上式中的$U$是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们希望将数据从$n$维降至$k$维，我们只需要从$U$中选取前$k$个向量，获得一个$n\times k$维度的矩阵，我们用$U_{reduce}$表示，然后通过如下计算获得要求的新特征向量$z^{(i)}$:$$z^{(i)}=U_{reduce}^T\ast x^{(i)}$$，其中$x$是$n\times 1$维的，因此结果为$k\times 1$维度。

低维向高维：$x$为2维，$z$为1维，$z=U_{reduce}^{T}x$，相反的方程为：$x_{appox}=U_{reduce}\cdot z$,$x_{appox}\approx x$。

高斯分布&&异常检测

高斯分布，也称为正态分布，例如变量 $x$ 符合高斯分布 $x\sim N(\mu ,{\sigma }^2)$则其概率密度函数为：

$p(x,\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$
$\mu$和${\sigma }^2$的计算方法如下：对阴影部分积分值为1
$\mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)}$ ${\sigma }^2=\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu {)}^2$

异常检测算法：对于给定的数据集 $x^{(1)},x^{(2)},...,x^{(m)}$，我们要针对每一个特征计算 $\mu$ 和 ${\sigma }^2$ 的估计值：

​ ${\mu }_j=\frac{1}{m}\sum _{i=1}^m{x}_j^{(i)}$ ${\sigma }_j^2=\frac{1}{m}\sum _{i=1}^m(x_j^{(i)}-{\mu }_j{)}^2$

获得了平均值和方差的估计值，给定新的一个训练实例，根据模型计算 $p(x)$

​ $p(x)=\prod _{j=1}^{n}p(x_j;{\mu }_j,{\sigma }_j^2)=\prod _{j=1}^1\frac{1}{\sqrt{2\pi }{\sigma }_j}exp(-\frac{(x_j-{\mu }_j{)}^2}{2{\sigma }_j^2})$

当$p(x)<\epsilon$时，为异常。

异常检测VS监督学习

异常检测	监督学习
非常少量的正向类（异常数据 $y=1$）, 大量的负向类（$y=0$）	同时有大量的正向类和负向类
许多不同种类的异常，非常难。根据非常 少量的正向类数据来训练算法。	有足够多的正向类实例，足够用于训练 算法，未来遇到的正向类实例可能与训练集中的非常近似。
未来遇到的异常可能与已掌握的异常、非常的不同。
例如： 欺诈行为检测 生产（例如飞机引擎）检测数据中心的计算机运行状况	例如：邮件过滤器 天气预报 肿瘤分类

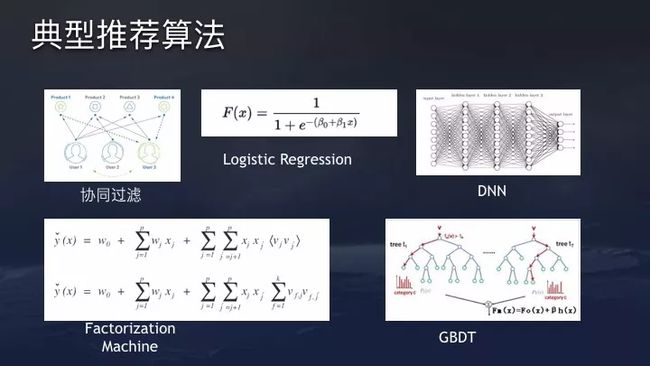
今日头条推荐算法详解

_2021级_ 第12周_学习总结

21.11.22-21.11.28

推荐系统

协同过滤Collaborative filtering, CF

CF有两种基本方法：基于用户的协同过滤和基于项目的协同过滤。 步骤：

• 了解数据库中有多少用户/项目与给定的用户/项目相似。
• 考虑到与它类似的用户/项目的总权重，评估其他用户/项目，来预测你会给该产品用户的打分。

在协同过滤从算法中，通常不使用方差项，算法会自动学得。

协同过滤优化目标：

• 给定$x^{(1)},...,x^{(n_m)}$，估计${\theta }^{(1)},...,{\theta }^{(n_u)}$：

• 给定${\theta }^{(1)},...,{\theta }^{(n_u)}$，估计$x^{(1)},...,x^{(n_m)}$：同时最小化$x^{(1)},...,x^{(n_m)}$和${\theta }^{(1)},...,{\theta }^{(n_u)}$：

  

协同过滤算法使用步骤如下：

1. 初始 $x^{(1)},x^{(1)},...x^{(nm)},{\theta }^{(1)},{\theta }^{(2)},...,{\theta }^{(n_u)}$为一些随机小值

2. 使用梯度下降算法最小化代价函数

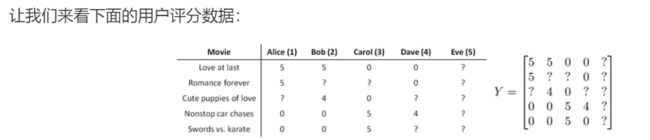
3. 在训练完算法后，我们预测$({\theta }^{(j)}{)}^T{x}^{(i)}$为用户 $j$ 给电影 $i$ 的评分

通过这个学习过程获得的特征矩阵包含了有关电影的重要数据，这些数据不总是人能读懂的，但是我们可以用这些数据作为给用户推荐电影的依据。

例如，如果一位用户正在观看电影 $x^{(i)}$，我们通过两部电影的特征向量之间的距离$\Vert x^{(i)}-x^{(j)}\Vert$的大小可以寻找另一部电影$x^{(j)}$。

低秩矩阵分解

均值归一化

大规模学习

大型数据集的学习

如果我们有一个低方差的模型，增加数据集的规模可以获得更好的结果。我们应该怎样应对一个有100万条记录的训练集？

以线性回归模型为例，每一次梯度下降迭代，我们都需要计算训练集的误差的平方和，如果我们的学习算法需要有20次迭代，这便已经是非常大的计算代价。

首先应该做的事是去检查一个这么大规模的训练集是否真的必要，也许只用1000个训练集也能获得较好的效果，同时可以绘制学习曲线来帮助判断。

随机梯度下降法

如果一定需要一个大规模的训练集，可以使用随机梯度下降法来代替批量梯度下降法。

在随机梯度下降法中，定义代价函数为一个单一训练实例的代价

随机梯度下降算法在每一次计算之后便更新参数 $\theta$ ，而不需要首先将所有的训练集求和，在梯度下降算法还没有完成一次迭代时，随机梯度下降算法便已经走出了很远。但是这样的算法存在的问题是，不是每一步都是朝着”正确”的方向迈出的。因此算法虽然会逐渐走向全局最小值的位置，但是可能无法站到那个最小值的那一点，而是在最小值点附近徘徊。

小批量梯度下降

小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法，每计算常数$b$次训练实例，便更新一次参数 $\theta$ 。

令 $b$ 在 2-100 之间。这样做的好处在于可以用向量化的方式来循环 $b$个训练实例，如果我们用的线性代数函数库比较好，能够支持并行处理，那么算法的总体表现将不受影响（与随机梯度下降相同）。

随机梯度下降收敛

在批量梯度下降中，我们可以令代价函数$J$为迭代次数的函数，绘制图表，根据图表来判断梯度下降是否收敛。但是，在大规模的训练集的情况下，这是不现实的，因为计算代价太大了。

每一次更新 $\theta$ 之前都计算一次代价，然后每$x$次迭代后，求出这$x$次对训练实例计算代价的平均值，然后绘制这些平均值与$x$次迭代的次数之间的函数图表。

当我们绘制这样的图表时，可能会得到一个颠簸不平但是不会明显减少的函数图像（如上面左下图中蓝线所示）。我们可以增加$\alpha$来使得函数更加平缓，能看出下降的趋势（如上面左下图中红线所示）；或者可能函数图表仍然是颠簸不平且不下降的（如洋红色线所示），那么我们的模型本身可能存在一些错误。

如果我们得到的曲线如上面右下方所示，不断地上升，那么可能会需要选择一个较小的学习率$\alpha$。

在线学习

如果有一个由连续的用户流引发的连续的数据流，进入你的网站，我们可以使用一个在线学习机制，从数据流中学习用户的偏好，然后使用这些信息来优化一些关于网站的决策。

一个算法来从中学习的时候来模型化问题在线学习算法指的是对数据流而非离线的静态数据集的学习。许多在线网站都有持续不断的用户流，对于每一个用户，网站希望能在不将数据存储到数据库中便顺利地进行算法学习。

一旦对一个数据的学习完成了，我们便可以丢弃该数据，不需要再存储它了。这种方式的好处在于，我们的算法可以很好的适应用户的倾向性，算法可以针对用户的当前行为不断地更新模型以适应该用户。

我们所使用的这个算法与随机梯度下降算法非常类似，唯一的区别的是，我们不会使用一个固定的数据集，我们会做的是获取一个用户样本，从那个样本中学习，然后丢弃那个样本并继续下去，在线学习的一个优点就是，如果有一个变化的用户群，在尝试预测的事情，在缓慢变化，就像你的用户的品味在缓慢变化，这个在线学习算法，可以慢慢地调试你所学习到的假设，将其调节更新到最新的用户行为

映射化简和数据并行

映射化简和数据并行对于大规模机器学习问题而言是非常重要的概念。之前提到，如果我们用批量梯度下降算法来求解大规模数据集的最优解，我们需要对整个训练集进行循环，计算偏导数和代价，再求和，计算代价非常大。如果我们能够将我们的数据集分配给不多台计算机，让每一台计算机处理数据集的一个子集，然后我们将计所的结果汇总在求和。这样的方法叫做映射简化。

案例

滑动窗口

滑动窗口是一项用来从图像中抽取对象的技术。假使我们需要在一张图片中识别行人，首先要做的是用许多固定尺寸的图片来训练一个能够准确识别行人的模型。然后我们用之前训练识别行人的模型时所采用的图片尺寸在我们要进行行人识别的图片上进行剪裁，然后将剪裁得到的切片交给模型，让模型判断是否为行人，然后在图片上滑动剪裁区域重新进行剪裁，将新剪裁的切片也交给模型进行判断，如此循环直至将图片全部检测完。一旦完成后，我们按比例放大剪裁的区域，再以新的尺寸对图片进行剪裁，将新剪裁的切片按比例缩小至模型所采纳的尺寸，交给模型进行判断，如此循环。

滑动窗口技术也被用于文字识别，首先训练模型能够区分字符与非字符，然后，运用滑动窗口技术识别字符，一旦完成了字符的识别，我们将识别得出的区域进行一些扩展，然后将重叠的区域进行合并。接着我们以宽高比作为过滤条件，过滤掉高度比宽度更大的区域（认为单词的长度通常比高度要大）。下图中绿色的区域是经过这些步骤后被认为是文字的区域，而红色的区域是被忽略的。

获取大量数据和人工数据

以我们的文字识别应用为例，我们可以字体网站下载各种字体，然后利用这些不同的字体配上各种不同的随机背景图片创造出一些用于训练的实例，这让我们能够获得一个无限大的训练集。这是从零开始创造实例。
另一种方法是，利用已有的数据，然后对其进行修改，例如将已有的字符图片进行一些扭曲、旋转、模糊处理。只要我们认为实际数据有可能和经过这样处理后的数据类似，我们便可以用这样的方法来创造大量的数据。
有关获得更多数据的几种方法：

1. 人工数据合成

2. 手动收集、标记数据

3. 众包