蓝桥杯AcWing学习笔记 6-1双指针的学习（附相关蓝桥真题：日志统计、完全二叉树的权值）

有参加蓝桥杯的同学可以给博主点个关注，博主也在准备蓝桥杯，可以跟着博主的博客一起刷题。

蓝桥杯

我的AcWing

题目及图片来自蓝桥杯C++ AB组辅导课

双指针

什么是双指针算法呢？

大部分双重循环是下面这样：

for (int i = 0; i < n; i++) {
	for (int j = 0; j < n; j++) {
		...
	}
}

↑ 时间复杂度为$O(N^2)$

但是它可以优化为下面这样的形式，把i和j写在一块：

for (int i = 0, j = 0; i < n; i++) {
	while (j < i) j++;
}

虽然看着还是两重循环，但是i和j只增加不减少，因此两个循环i和j最多只会增加1，因此时间复杂度为$O(N)$

所有这样的题目都可以统称为双指针算法，其实就是一个简单的优化。

第九届2018年蓝桥杯真题

AcWing 1238. 日志统计

JavaB组第8题

如果用暴力的话我们应该枚举两重循环，一重枚举时间，一重枚举id。

暴力伪代码

for (时间段) {
	Arrays.fill(cnt, 0); // 数组初始化为0
	for (id) {
		cnt[id]++;
		if (cnt[id] >= k) st[id] = ture; // 如果是热帖 标记为true
	}
}

在我们枚举时间段时，会发现有很大一部分是重复的：

假设我们已经统计了上面区间的id次数，那我统计下面区间id次数，我们可以直接把开头去掉，把结尾加上即可：

cnt[id[i]]--，cnt[id[j]]++

优化

for (时间段) {
	cnt[id[i]]--; // 减去开头
	cnt[id[j]]++; // 加上结尾
}

时间复杂度优化成了$O(N)$

排序+双指针

① 先将所有的点赞数量按照时间顺序排好

② 通过双指针i和j维护长度不大于d的区间，并记录该区间的中所有帖子获得的赞数

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.Arrays;

public class Main {

    static int N = 100010;
    static PII[] logs = new PII[N];
    static int[] cnt = new int[N];
    static boolean[] st = new boolean[N]; // 记录每个帖子是否是热帖

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        String[] s1 = in.readLine().split(" ");
        int n = Integer.parseInt(s1[0]);
        int d = Integer.parseInt(s1[1]);
        int k = Integer.parseInt(s1[2]);
        for(int i = 0; i < n; i++) {
            String[] s2 = in.readLine().split(" ");
            int ts = Integer.parseInt(s2[0]);
            int id = Integer.parseInt(s2[1]);
            logs[i] = new PII(ts, id);
        }
        
        Arrays.sort(logs, 0, n);
        
        for(int i = 0, j = 0; i < n; i++) {
            int id = logs[i].id;
            cnt[id]++; // 记录每个id赞的个数
            
            while(logs[i].ts - logs[j].ts >= d) { // 如果时间跨度大于等于d
                cnt[logs[j].id]--; // 减去开头
                j++; // 加上结尾
            }
            if(cnt[id] >= k) st[id] = true;
        }
        
        for(int i = 0; i <= 100000; i++) {
            if(st[i]) System.out.println(i);
        }
    }
}

class PII implements Comparable<PII> {
    int ts;
    int id;

    public PII(int ts, int id) {
        this.ts = ts;
        this.id = id;
    }

    @Override
    public int compareTo(PII o) {
        return Integer.compare(ts, o.ts); // 基于时间ts排序
    }
}

第十届2019年蓝桥杯真题

AcWing 1240. 完全二叉树的权值

JavaA组第6题

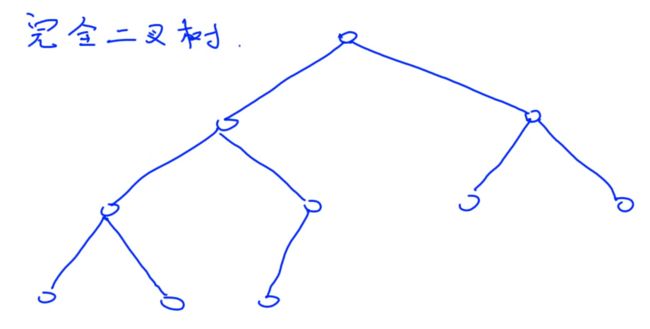
完全二叉树：除了最后一层，前面每一层的节点都有两个儿子，最后一层所有节点都集中在最左边。

每个节点都有权值，求权值和最大的层数，如果有层数权值相同，则输出深度较小的层数。

我们把样例画出来：

我们观察一下每个根节点的下标i，是1 2 4 8：

我们可以初步写出一个for循环：for (d = 1; i = 1; i <= n; d++, i *= 2) 循环层，d是深度，我们需要求这一层的总和，i是起点，长度是2^d-1，我们只需要求从i开始，长度是2^d-1的总和即可。

伪代码

for (d = 1; i = 1; i <= n; d++, i *= 2) {
	s = 0
	for (j = i; j < i + Math.pow(2, d - 1) && j <= n; j++) s += a[j];
	更新max
}

第二重循环可能有点难看懂，此时j代表着第d层的下标，假如我们要遍历第三层，那么起点i是4，层数d是3，$2^{d-1}$是4个数，也就是遍历下标4 ~ 7这4个数；j <= n是对最后一行的边界特判。

看起来是两重循环，但是每个数只会被遍历一次，总共时间复杂度$O(N)$

完整代码

import java.util.Scanner;

public class Main {

    static final int N = 100010;
    static int[] a = new int[N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++) a[i] = sc.nextInt();
        
        long max = Long.MIN_VALUE;
        int depth = 0;
        
        for (int d = 1, i = 1; i <= n; d++, i *= 2) {
            long s = 0;
            for (int j = i; j < i + Math.pow(2, d - 1) && j <= n; j++) {
                s += a[j];
            }
            if (s > max) {
                max = s;
                depth = d;
            }
        }
        System.out.print(depth);
    }
}

有对代码不理解的地方可以在下方评论