图解算法:LIS问题,单调队列+二分优化
关注下方公众号,分享硬核知识
作者 | 小K
出品 | 公众号:小K算法 (ID:xiaok365)
01
故事起源
LIS:Longest Increasing Subsequence(最长递增子序列)。
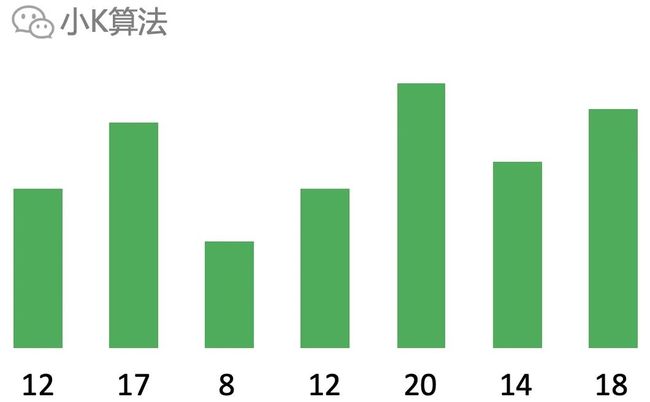
给你一个整数数组,如何求出其中最长的严格递增子序列的长度?
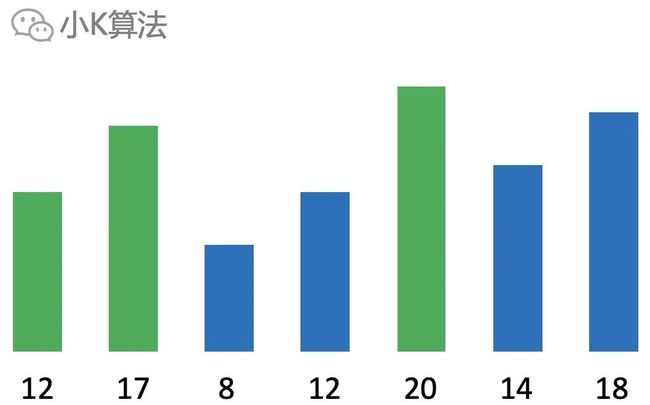
比如下面绿色和蓝色都是符合要求的子序列,但蓝色的子序列更长,所以最大长度为4。
02
思考
要求最长子序列的长度,那肯定要先找出这个最长的子序列。比如下面蓝色的子序列就是我们要找的序列。
所以整个数组的元素就可以分为两类,一类是属于最终的目标序列,一类是不属于最终的目标序列。
那我们要怎么确定一个元素是否应该选取到目标序列呢?咱们还是从小规模开始分析吧,懂的都懂(小K式思维法)。
03
小规模分析
3.1
一个元素
如果只有一个元素,那自然是要选了,最大长度为1。
3.2
两个元素
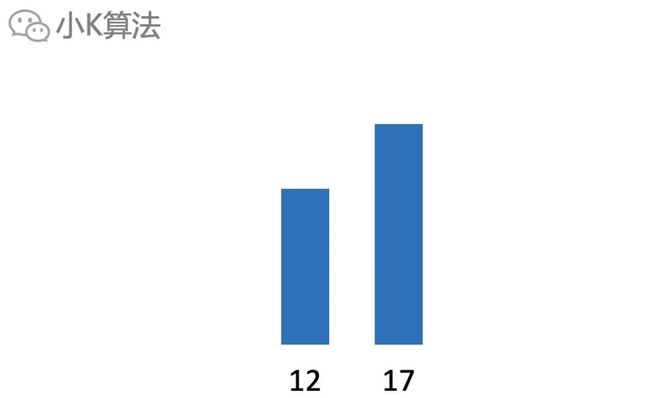
如果再加第2个元素,满足递增子序列,两个都选,最大长度为2。
如果再加第2个元素是这样的,选了第1个就选不了第2个,不选第1个就可以选第2个。但怎么选都只能选1个,最大长度是1。
3.3
三个元素
如果选取了前面2个元素,再加第3个元素,已经无法再选取,最大长度为2。
如果前面只选取第1个元素,再加第3个元素,可以选取第3个元素,最大长度也为2。
请问你发现什么规律了吗?
因为是递增序列,所以一个元素能不能选,跟之前选择的最后一个元素有关。如果大于最后一个元素就可以选择,如果小于或等于就无法选择。
04
抽象分析
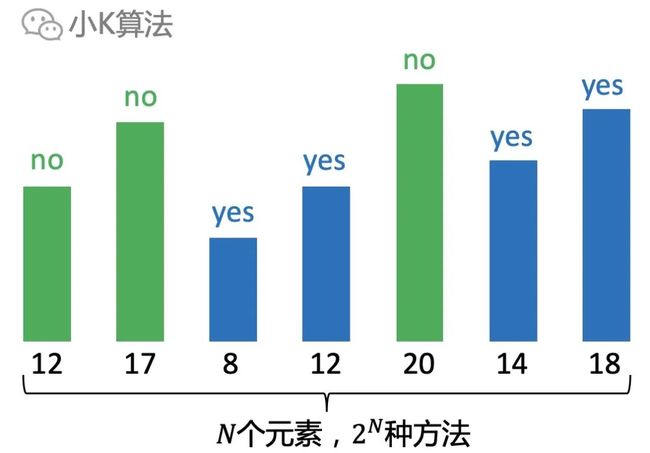
如果不考虑任何规律,每个元素可以选或不选, 个元素就有 种选取方法。当然要保证递增序列,就可以排除很多不合理的情况,但规模依然很大。
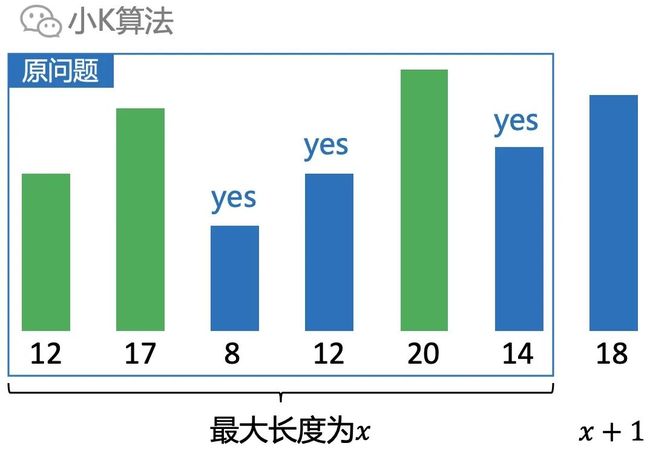
假设原问题已经找到了最大的子序列,现在我再给你加一个元素进来,选还是不选呢?
如果原问题最大长度为X,那选择最新的元素的前提就是最大长度能变成X+1,如果选了长度没变甚至更小那肯定就不选。说明新的元素一定要能接在之前的最优解后面才可选取。
数据规模每扩大一次,最优解也是在之前的最优解上面扩充。
再根据第3小节的分析,对于每一个最优解,其实我们并不关注前面的X-1个元素是怎么选择的,只关注第X个元素是选的啥,那就可以从小规模开始枚举,求出以每个元素作为结尾时的最大长度,这样就可以递推出更大规模的最优解,这其实就是动态规划的思想。
05
动态规划
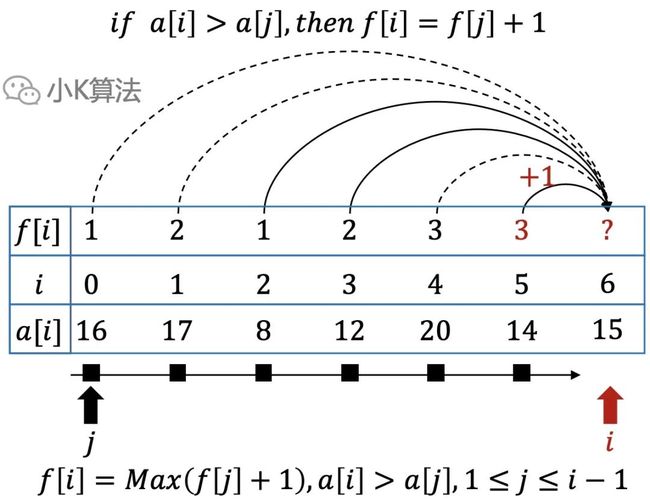
设 表示以第 个元素为结尾,能得到的最大的长度,那么 一定是从之前的某个最优解递推过来。
即。
代码实现
void dp() {
int a[100], f[100], ans = 0;
for (int i = 0; i < n; ++i) {
cin >> a[i];
f[i] = 1;
for (int j = 0; j < i; ++j) {
if (a[j] < a[i]) {
f[i] = max(f[i], f[j] + 1);
}
}
ans = max(ans, f[i]);
}
cout << ans << endl;
}
动态规划的复杂度为 ,当 很大时效率就很低了,那能不能继续优化呢,这就还得继续找本质规律。
06
哪里有问题呢
6.1
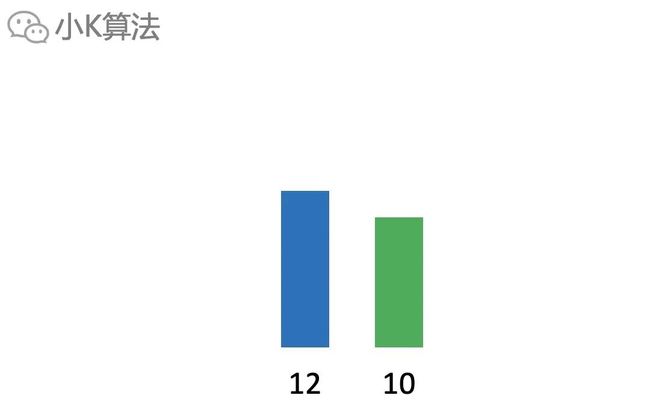
长度相等,高度更矮
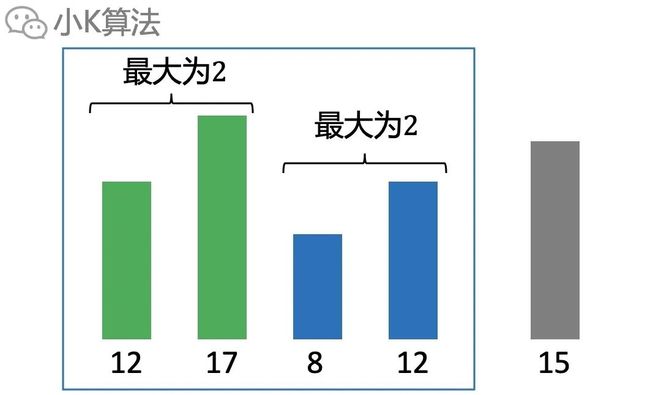
如果前4个元素是这样的:
选取前2个长度为2,选取后2个长度也是2,但明显选取后2个更好,因为末位的高度更矮。
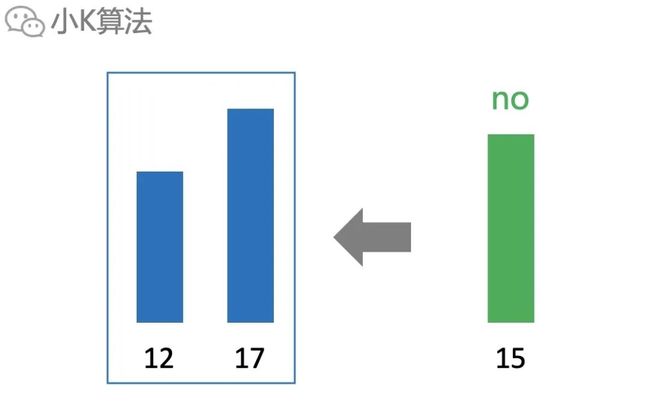
如果再加一个元素15,那就可以接在后面变成更大的长度3,但如果选择前面两个就不行。说明前面2个可以直接抛弃。
6.2
长度更长,高度更矮
如果前5个元素是这样的:
选取前2个长度为2,选取后3个长度为3,而且高度更矮,明显更优。说明前面2个也应该直接抛弃。
6.3
长度更长,高度更高
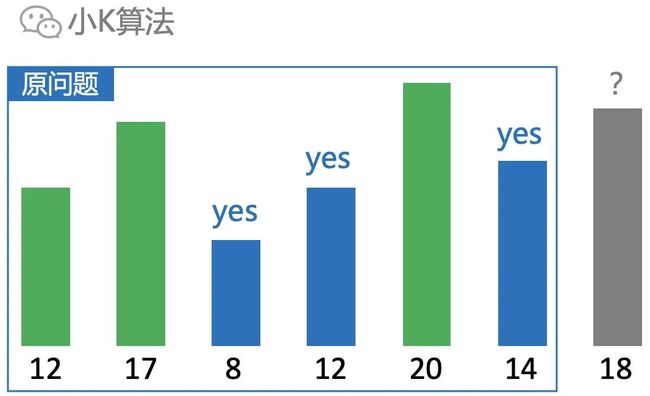
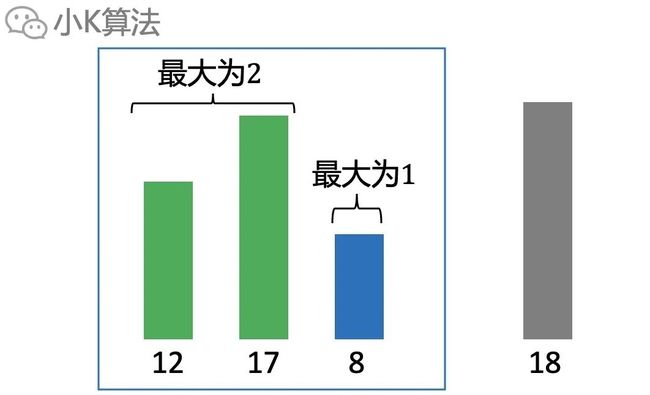
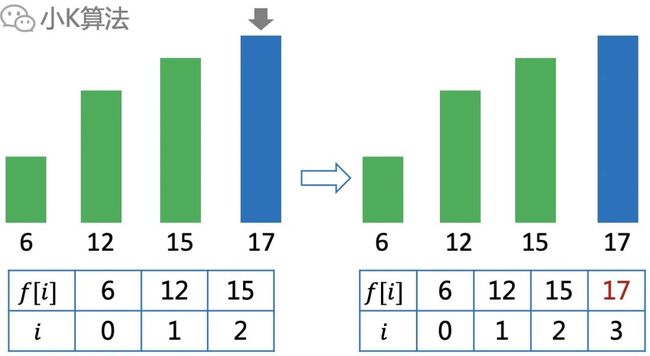
如果前3个元素是这样的:
选取前2个长度为2,选取第3个长度为1。虽然前面的高度更高了,但长度也更大,不能直接抛弃。
比如再来一个元素18,就可以直接接在前面2个之后,长度为3。
6.4
公式分析
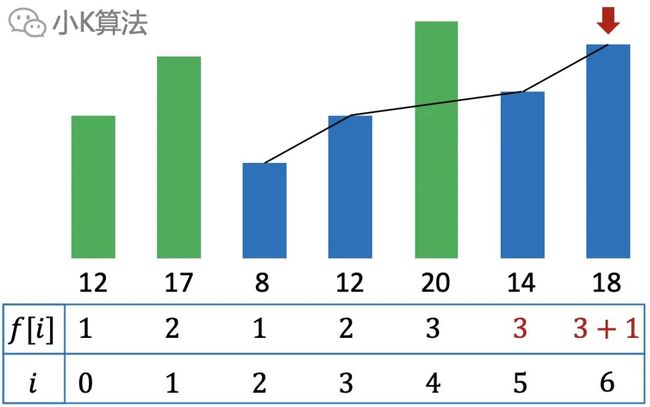
再回到之前的DP递推公式,在求每一个 时,其实都是从之前找一个符合要求的最大的 。之前的方法是枚举每一个,这样查找自然效率就比较低,那能否更快的找到我们想要的 呢?
6.1~6.3分析了不同的情况,其实我们只需要保留6.3中的情况,长度更长,末位更高。把这些单独拿出来再看,其实就是一个单调上升队列,长度和高度同步单调递增。对于一个单调有序的队列,你会怎么查找呢,当然最快就是二分查找了啊。
再看上面的 和 其实可以放在一起,这时 的含义就变成长度为 时末尾的最小值,我们只需要维护这个一维队列即可。
6.5
如何维护
从左开始扫描每一个数,如果当前数 等于队尾的数则直接抛弃。
如果当前数 大于列尾的数,就直接加入队尾。
如果当前数 小于列尾的数,就通过二分查找,找到刚好大于 的数 ,并用 替换 。
这样最终的 队列的长度就是我们要找的最长递增子序列长度。
07
算法实现
在通过二分查找时,要注意几个细节,就是 指针最终停留的位置有不同的情况。
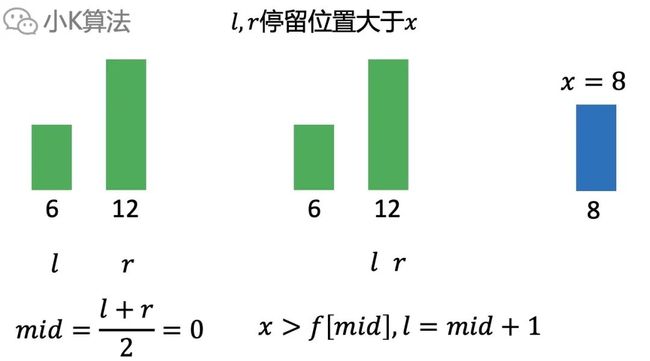
如下 。
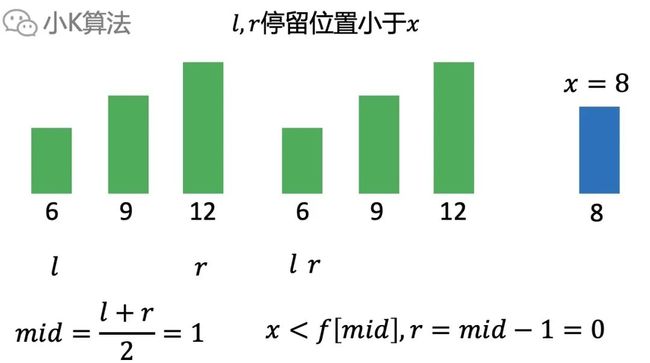
如下 。
如下 。
所以在更新的时候需要判断。
代码实现
void greed() {
int f[1000], x, num = 0;
f[0] = 0;
for (int i = 0; i < n; ++i) {
cin >> x;
if (x == f[num]) {
continue;
}
if (x > f[num]) {
f[++num] = x;
continue;
}
int l = 0, r = num, mid;
while (l < r) {
mid = (l + r) / 2;
if (f[mid] == x) {
l = mid;
break;
}
if (f[mid] < x) {
l = mid + 1;
} else {
r = mid - 1;
}
}
//最后停留位置,>,<,=都有可能,小于更新当前位置,大于更新后一位置
if (x < f[l]) { f[l] = x; }
else if (x > f[l]) {
f[l + 1] = x;
}
}
cout << num << endl;
}
08
总结
这是一道比较经典的动态规划问题,公式也很简单。但不论是通过原问题模拟过程的分析,还是直接通过递推公式分析,都可以发现有很多冗余的操作,这些就是我们优化的切入点,单调队列在DP中是很常用的优化技巧,而单调有序性就可以结合二分查询提高效率。以后可以再给大家讲讲其它的几种常用DP优化技巧。
本文原创作者:小K,一个思维独特的写手。
文章首发平台:微信公众号【小K算法】。
如果喜欢小K的文章,请点个关注,分享给更多的人,小K将持续更新,谢谢啦!
关注下方公众号,分享硬核知识
关注我,涨知识
原创不易,感谢分享
转发,点赞,在看!
▼
往期精彩回顾
▼
算法面试题:均分纸牌
图解算法:冒泡排序
巴什博弈:取石子游戏
分享给更多朋友,转发,点赞,在看