地毯--二维差分

ACM专题学习一

题目

在 n×n 的格子上有 m 个地毯。

给出这些地毯的信息，问每个点被多少个地毯覆盖。

输入格式

第一行，两个正整数n (1≤n≤1000)、m (1≤m≤10^5)，意义如题所述。

接下来 m 行，每行两个坐标(x1​,y1​) 和 (x2​,y2​)，代表一块地毯，左上角是(x1​,y1​)，右下角是 (x2​,y2​)。

输出格式

输出 n 行，每行 n 个正整数。

第 i 行第 j 列的正整数表示 (i,j)这个格子被多少个地毯覆盖。

输入样例

4 3
1 1 3 3
2 2 4 4
3 1 4 3

输出样例

1 1 1 0
1 2 2 1
2 3 3 1
1 2 2 1

思路

铺一个地毯就在数组部分加上1，可以用二维差分。

下面介绍两种标记方法

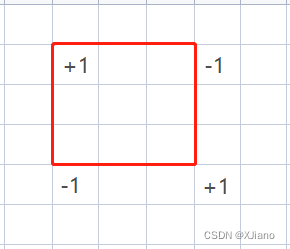
第一种是正常的二维差分，普遍的思路，这里不用求差分数组，因为原数组里的元素都是0。把原数组当做差分数组，在四个点标记操作，最后求前缀和就行了。

代码

#include
#include
using namespace std;
int b[1005][1005]={0},n,m,i,j,x1,y1,x2,y2;
void insert(int x1,int y1,int x2,int y2)
{  								// 差分数组四点标记
    b[x1][y1] += 1;
    b[x1][y2+1] -= 1;
    b[x2+1][y1] -= 1;
    b[x2+1][y2+1] += 1;
	}
int main()
{ 
    int x1,y1,x2,y2,num;
    scanf("%d%d",&n,&m);
    for(i=0;i>x1>>y1>>x2>>y2;
        insert(x1,y1,x2,y2);
    }
    b[0][0]=0;
    for (int i = 1; i <= n ;i++)
    {
    	b[i][0]=0;
        for(int j = 1; j <= n ; j++)
        {
        	b[0][j]=0;
            b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1] ; //差分数组求前缀和
            printf("%d",b[i][j]);
		    if(j!=n)printf(" ");
        }
        if(i!=n)printf("\n");
    }
  
}

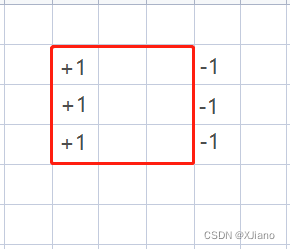
第二种方法是把二维数组看做一维数组，用一维的方法求差分数组，然后进行两两标记，在地毯的每行进行标记，最后做一维前缀和。这道题不用求差分数组。

代码

#include
#include
using namespace std;
int a[1005][1005];
int x1,x2,y1,y2; 
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=0;i>x1>>y1>>x2>>y2;
        for(int j=x1;j<=x2;j++)//对行进行操作
        {
            a[j][y1]++;
            a[j][y2+1]--;
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)//求前缀和
        {
            a[i][j] +=a[i][j-1];
            cout<