第十二届蓝桥杯C/C++大学B组省赛题解

A、空间

  小蓝准备用 256MB 的内存空间开一个数组，数组的每个元素都是32位二进制整数，如果不考虑程序占用的空间和维护内存需要的辅助空间，请问256MB的空间可以存储多少个 32 位二进制整数？

题解
1MB=1024KB
1KB=1024B
1B=8位
每个元素都是32位二进制整数即每个元素都是4字节
256 * 1024 * 1024/4=67108864
答案： 67108864

C、直线

  在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，那么这些点中任意两点确定的直线是同一条。
  给定平面上 2 × 3 个整点 $\{(x,y)|0\le x<2,0\le y<3,x\in Z,y\in Z\}$ ，即横坐标是 0 到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2) 之间的整数的点。这些点一共确定了 11 条不同的直线。
  给定平面上 20 × 21 个整点 $\{(x,y)|0\le x<20,0\le y<21,x\in Z,y\in Z\}$ ，即横坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20) 之间的整数的点。请问这些点一共确定了多少条不同的直线？

题解
由于直线的类型比较多，这里选择y=kx+b作为直线方程，$k=(y_1-y_2)/(x_1-x_2)$，计算每两个点的斜率和截距，有多少种不同的斜率和截距就有多少条不同的直线，垂直于x轴的直线斜率不存在，不用计算，最后加上即可，本题要加20
答案：40257

#include
#include
#include
#include
using namespace std;

struct node{
    double k,b;
    bool operator<(const node&w)const
    {
        if(k!=w.k)return k<w.k;
        return b<w.b;
    }
};
vector<node>vec;

int main()
{
    int sum=1;
    for(int x1=0;x1<20;++x1)
        for(int y1=0;y1<21;++y1)
            for(int x2=0;x2<20;++x2)
                for(int y2=0;y2<21;++y2)
                    if(x1!=x2)
                    {
                        double k=(double)(y1-y2)/(x1-x2);
                        double b=y1-k*x1;
                        vec.push_back({k,b});
                    }
    sort(vec.begin(),vec.end());
    for(int i=1;i<vec.size();++i)
        if(fabs(vec[i].k-vec[i-1].k)>=1e-6||fabs(vec[i].b-vec[i-1].b)>=1e-6)
            ++sum;
    cout<<sum+20<<endl;
    return 0;
}

D、货物摆放

  小蓝有一个超大的仓库，可以摆放很多货物。
  现在，小蓝有n箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长,宽、高。
  小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆L、W、H的货物，满足n=L×W×H。
  给定n,请问有多少种堆放货物的方案满足要求。
  例如，当n=4时，有以下6种方案: 1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1。
  请问，当n = 2021041820210418（注意有16位数字)时，总共有多少种方案?
  提示:建议使用计算机编程解决问题。

答案：2430

#include
#include
using namespace std;

typedef long long ll;
vector<ll>prime;

int main()
{
    int sum=0;
    ll n=2021041820210418;
    for(ll i=1;i*i<=n;++i)
    {
        if(n%i==0)
        {
            prime.push_back(i);
            if(n/i!=i)
                prime.push_back(n/i);
        }
    }
    for(ll x:prime)
        for(ll y:prime)
        {
            ll z=n/x/y;
            if(x*y*z==n)
                ++sum;
        }
    cout<<sum<<endl;
    return 0;
}

F、时间显示

【问题描述】
  小蓝要和朋友合作开发一个时间显示的网站。在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 1970 年 1 月 1 日 00:00:00 到当前时刻经过的毫秒数。
  现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。
  给定一个用整数表示的时间，请将这个时间对应的时分秒输出。
【输入格式】
  输入一行包含一个整数，表示时间。
【输出格式】
  输出时分秒表示的当前时间，格式形如HH:MM:SS，其中 HH 表示时，值为 0 到 23，MM 表示分，值为 0 到 59，SS 表示秒，值为 0 到 59。时、分、秒不足两位时补前导 0。
【样例输入1】

46800999

【样例输出1】

13:00:00

【样例输入2】

1618708103123

【样例输出2】

01:08:23

【评测用例规模与约定】
  对于所有评测用例，给定的时间为不超过 $10^{18}$ 的正整数。

题解　　
总秒数对一天的秒数86400取余去除完整经过的天数，得到最后一天的秒数，最后一天的秒数除以3600求出经过的小时，对3600取余去除小时得到剩下的秒数，剩下的秒数除以60求出经过的分钟，对60取余去除分钟求出经过的秒

#include
#include
using namespace std;

typedef long long ll;

int main()
{
    ll n;
    scanf("%lld",&n);
    n=n/1000%86400;
    int h=n/3600;
    n%=3600;
    int m=n/60;
    int s=n%60;
    printf("%02d%02d%02d\n",h,m,s);
    return 0;
}

G、砝码称重

【问题描述】
你有一架天平和 N 个砝码，这 N 个砝码重量依次$W_1$,$W_2$,⋅⋅⋅,$W_N$。
请你计算一共可以称出多少种不同的正整数重量？
注意砝码可以放在天平两边。
【输入格式】
输入的第一行包含一个整数 N。
第二行包含 N 个整数：$W_1$,$W_2$,$W_3$,⋅⋅⋅,$W_N$。
【输出格式】
输出一个整数代表答案。
【样例输入】

3
1 4 6

【样例输出】

10

【样例说明】
能称出的 10 种重量是：1、2、3、4、5、6、7、9、10、11。
1 = 1；
2 = 6 − 4 (天平一边放 6，另一边放 4)；
3 = 4 − 1；
4 = 4；
5 = 6 − 1；
6 = 6；
7 = 1 + 6；
9 = 4 + 6 − 1；
10 = 4 + 6；
11 = 1 + 4 + 6。
【评测用例规模与约定】
对于 50% 的评测用例，1≤N≤15。
对于所有评测用例，1≤N≤100，N 个砝码总重不超过100000。

dp

dp[i][j]为在前i个砝码里选，称出重量为j的选法

重量为0一定能被称出

一个砝码有三种选择
不选：直接从dp[i-1][j]转移过来
放左边：相当于增重后重量为j，要判断j-a[i]是否已被称出，若是，则可以用之前的重量称出j，否则称不出，需要注意的是，遍历砝码是按顺序的，当j小于当前砝码的重量时，相当于当前砝码减重后称出j，即a[i]-j
放右边：相当于减重后重量为j，要判断j+a[i]是否已被称出，若是，则可以用之前的重量称出j，否则称不出，这里要注意极端情况，j加上当前砝码的重量最大为砝码总重的2倍，因此数组的重量维度要开到2倍，但超出砝码总重的部分一定为0值，不会影响结果
转移方程为dp[i][j]=dp[i-1][j]|dp[i-1][j+a[i]]|dp[i-1][abs(j-a[i])]

#include
#include
using namespace std;

const int N=110,M=2e5+10;//M=1e5+10
int a[N];
bool dp[N][M];

int main()
{
    int n,sum=0,ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&a[i]);
        sum+=a[i];
    }
    dp[0][0]=true;
    for(int i=1;i<=n;++i)
        for(int j=0;j<=sum;++j)
            dp[i][j]=dp[i-1][j]|dp[i-1][j+a[i]]|dp[i-1][abs(j-a[i])];  
        /*
        {
            dp[i][j]=dp[i-1][j]|dp[i-1][abs(j-a[i])];
            if(j+a[i]<=sum)dp[i][j]|=dp[i-1][j+a[i]];
        }
        */
    for(int i=1;i<=sum;++i)
        if(dp[n][i])++ans;
    printf("%d\n",ans);
    return 0;
}

库函数

参考文章https://www.acwing.com/solution/content/45929/

用bitset的第i位表示重量为i是否被称出

重量为0一定能被称出

左移表示用当前砝码增重，右移表示用当前砝码减重，先用所有砝码左移，再用所有砝码右移，保证小于0的重量是非法的且不会被保存，最后除重量为0外有多少被称出的就是答案

#include
#include
#include
using namespace std;

const int N=110,M=1e5+10;
int a[N];
bitset<M>S;

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;++i)
        scanf("%d",&a[i]);
    S[0]=1;
    for(int i=0;i<n;++i)
        S|=S<<a[i]; 
    for(int i=0;i<n;++i)
        S|=S>>a[i]; 
    printf("%d\n",S.count()-1);
    return 0;
}

H、杨辉三角形

【问题描述】
下面的图形是著名的杨辉三角形：

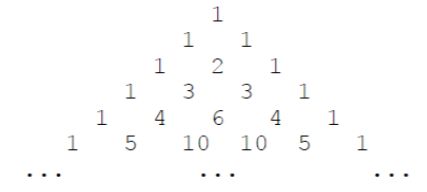
如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列：
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, …
给定一个正整数 N，请你输出数列中第一次出现 N 是在第几个数？
【输入格式】
输入一个整数 N。
【输出格式】
输出一个整数代表答案。
【样例输入】

6

【样例输出】

13

【评测用例规模与约定】
对于 20% 的评测用例，$1\le N\le 10$；
对于所有评测用例，$1\le N\le 10^9$。

题解
杨辉三角左右对称，每个数第一次出现一定在左边或中间，因此可以去掉右边

性质
第n行第m列的数为$C_n^m$(0≤m≤n)
同一列的数从上往下递增
同一行的数从右往左递减
每一斜行从右上往左下递增，以k为某斜行的下标，该斜行上所有数的列下标均为k，最小值为$C_{2k}^k$，第i个数为$C_{2k+i-1}^k$

思路
n最大为$10^9$，$C_{34}^{17}>10^9$，$C_{32}^{16}<10^9$，因此枚举前16斜行

二分当前斜行
左边界：2k
右边界：右边界不能小于左边界，当n>2k时，极端情况为$C_n^1=n$，因此为max(n,l)

假设找到n，n同一行左边的数都比它小，这些数按斜行往下递增才可能等于n，但不是第一次出现，因此要从下往上枚举斜行

当找到n时，l为上面有多少行，第一行有1个数，第二行有2个数…第n行有n个数，上面有$\frac{l(1+l)}{2}$个数，k为n的列下标，n在这一行为第k+1个数，因此n是第$\frac{l(1+l)}{2}+k+1$个数

#include
#include
using namespace std;

typedef long long ll;
int n;

ll C(int a,int b)
{
    ll res=1;
    for(int i=a,j=1;j<=b;--i,++j)
    {
        res=res*i/j;
        if(res>n)return res;//大于n无意义且防止爆long long
    }
    return res;
}
bool check(int k)
{
    int l=2*k,r=max(n,l);
    while(l<r)
    {
        int mid=l+r>>1;
        if(C(mid,k)>=n)r=mid;
        else l=mid+1;
    }
    if(C(l,k)!=n)return false;
    printf("%lld\n",1ll*l*(1+l)/2+k+1);
    return true;
}
int main()
{
    scanf("%d",&n);
    for(int i=16;;--i)
        if(check(i))break;
    return 0;
}