《R3Det：Refined Single-Stage Detector with Feature Refinement for Rotating Object》论文笔记

参考代码：

1. TF实现版本：R3Det_Tensorflow
2. Pytorch实现版本：r3det-on-mmdetection
3. 旋转检测算法总结：RotationDetection

1. 概述

导读：这篇文章提出了一种级联优化的旋转目标检测算法。这篇文章的检测算法可以看作是单阶段的（类似RefineDet）检测算法。算法的第一级回归用于生成带旋转角度的roi proposal（也可以称之为带旋转角度的anchor），在之后的优化级中去迭代优化上一级生成的roi proposal。需要注意的是文章的算法在检测目标的优化阶段对特征图进行了优化（也就是文章提到的特征对齐操作，feature alignment operator），从而帮助获取更加精确的目标位置定位。对于损失函数部分，文章引入倾斜矩形的交叠面积作为目标边界框损失的加权项，从而与Smooth L1损失进行互补，兼顾不同IoU情况下的回归损失。注意：需要去读论文源码的同学请阅读TF版本的代码实现，Pytorch版本的代码存在较多遗漏。

需要注意的是，文章中使用的级联优化的方式对旋转目标框进行回归，不过其在anchor机制上做了一些取巧的工作，文章比较了常用的anchor机制：水平anchor和带旋转角度的anchor，它们分别具有如下的特性：

• 1）水平anchor：在anchor数量少的情况下能获取更高的召回；
• 2）带角度的anchor：在密集场景下能获得更加的性能表现；

正是基于上述两种anchor的特性，文章在第一级直接采用水平anchor进行回归（没有针对角度设置anchor，角度直接进行回归），并在后面的优化级中对带旋转角度的roi proposal进行进一步优化，这样就很好兼顾了两种不同类型anchor的性质。

2. 方法设计

2.1 方法pipline

文章的算法pipeline总体上是一阶段的结构，网络在FPN输出结果上进行边界框预测，其结构见下图所示：

注意上图中绘制的网络结构，在第一阶段输出的分类和回归通道都是$5A$的，但是在后面的优化阶段中通道都变成了$5$，也就正如前文提到的一致，第一阶段主要就是用水平的anchor去生成带角度的roi proposal，之后再级联几个优化模块进行精细化回归。

上面的方法预测的是带有旋转角度的目标框，对此会对的目标可以描述为$(x,y,w,h,\theta )$，它们分别代表旋转矩形框的中心点坐标、宽高和角度信息。对于需要回归的变量描述为：
$$t_x=\frac{(x-x_a)}{w_a},t_y=\frac{(y-y_a)}{h_a}$$
$$t_w=log(\frac{w}{w_a}),t_h=log(\frac{h}{h_a}),t_{\theta }=\theta -{\theta }_a$$

2.2 Feature Refinement Module（FRM）

在进行边界框位置确定的时候，使用的是浮点数，但是实际上目标的位置一般都为定点的，这就导致了在级联优化和定位过程中没有对齐的情况。在两阶段的检测算法中，是使用如RoI Pooling这样的操作实现对齐。那么一个在一阶段的检测网络中怎么去实现特征的对齐呢？文章使用的方式——双线性插值。也就是下图中展示的：

那么对于插值的算子，可以描述为：
$$F=F_{lt}\ast A_{rb}+F_{rt}\ast A_{lb}+F_{rb}\ast A_{lt}+F_{lb}\ast A_{rt}$$
不同的插值方法对性能也是有不同的影响的，可参考下表：

上面插值计算过程中使用到的点是由上一阶段的预测网络提供的roi proposal，那么FRM模块的特征优化过程可以描述为：
$$F_{i+1}=FRM(B_i,S_i,\{P_2,\dots ,P_7\})$$
具体来讲就是使用上一级生成roi proposal的边界框位置和置信度去优化特征图，伪代码描述为：

对于这个模块如何嵌入到网络中的，可以参考下图：

对于该FRM模块的实现可以参考下面的代码实现：
def refine_feature_op(self, points, feature_map, name)

那么同样是特征对齐，文章的方法与RoI Pooling有着什么样的区别呢？对此，文章中将其归纳为如下2点：

• 1）计算效率不一样：RoI Pooling操作的是一个特征块，而文章提出的对齐方法操作的是5个点（4个顶点+1个中心点），自然计算的效率就高了很多了；
• 2）处理信息的范围不一样：RoI Pooling处理的是一个instance的特征，而文章的方法是在原特征图上进行对齐，因而可以看作是image层级的，同时还可以避免Faster RCNN中全连接的引入，减少计算量；

2.3 损失函数

文章的损失函数跟传统的检测损失函数是类似的，也是包含分类损失和边界框回归损失。只不过在回归损失的过程中兼容考虑了Smooth L1和倾斜举行的交叠面积（Skew IoU）。这里需要进行这样的考虑是因为Smooth L1损失函数和实际的Skew IoU度量并不是同步的，可以参考下面的情况：

从上图可以看到Smooth L1损失函数一致，但是Skew IoU差别比较大。对此进行统计分析，得到这两者之间的关系：

从上面的右图可以看到两者并不统一，对此文章提出将Skew IoU融入到边界框的回归过程中去，不过这里不是直接通过可导的形式添加，而是通过权重的形式添加，因而文章的损失函数可以描述为：
$$L=\frac{{\lambda }_1}{N}\sum _{n=1}^{N}ob{j}_n\frac{L_{reg}(v_n^{{}^{\prime }},v_n)}{|L_{reg}(v_n^{{}^{\prime }},v_n)|}|f(SkewIoU)|+\frac{{\lambda }_2}{N}\sum _{n=1}^N{L}_{cls}(p_n,t_n)$$
其中，回归部分的损失函数描述为（角度L1+边界框IoU损失）：
$$L_{reg}(v^{{}^{\prime }},v)=L_{smooth-l1}(v_{\theta }^{{}^{\prime }},v_{\theta })-IoU(v_{\{x,y,w,h\}}^{{}^{\prime }},v_{\{x,y,w,h\}})$$
那么对于这部分损失函数的实现可以参考：
def iou_smooth_l1_loss_(targets, preds, anchor_state, target_boxes, anchors, sigma=3.0, alpha=1.0, beta=1.0, is_refine=False)
其中的Skew IoU的计算描述为：
def iou_rotate_calculate2(boxes1, boxes2)
文章使用的是级联优化，那么多个层级（不同层级进行筛选的时候会使用不同的IoU阈值）的损失函数组织形式为：
$$L_{total}=\sum _{i=1}^N{\alpha }_i{L}_i$$
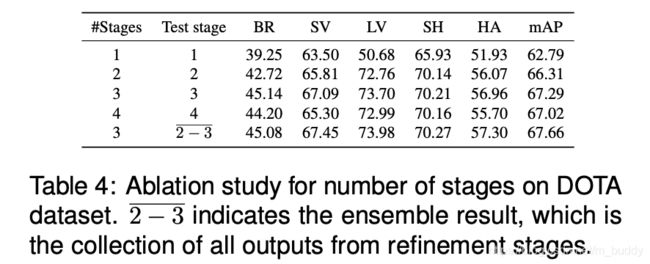
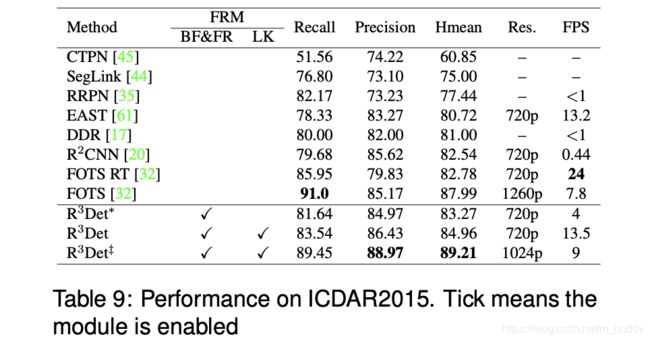
文章里面涉及的变量的消融实验：

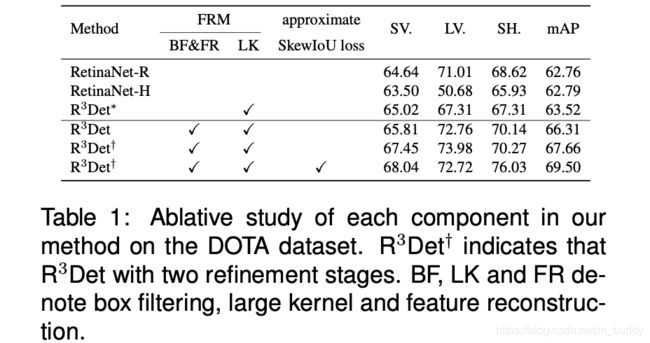
refine stage数量的影响：

3. 实验结果

DOTA数据集：

ICDAR 2015数据集：