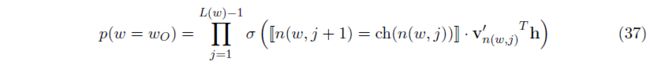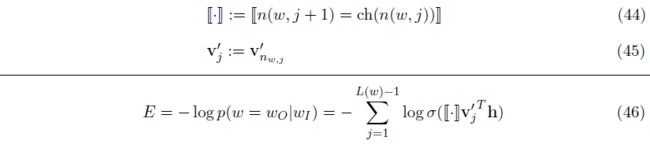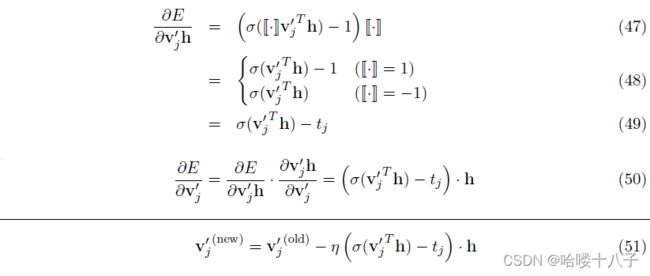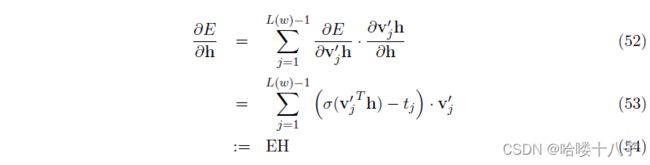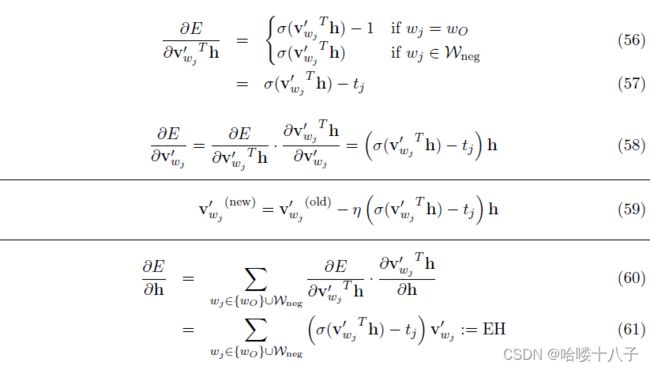《word2vec Parameter Learning Explained》论文笔记

word2vec Parameter Learning Explained

• Xin Rong([email protected])【致敬】
• arXiv:1411.2738v4 [cs.CL] 5 Jun 2016

Abstract

The word2vec model and application by Mikolov et al. have attracted a great amount of attention in recent two years. The vector representations of words learned by word2vec models have been shown to carry semantic meanings and are useful in various NLP tasks. As an increasing number of researchers would like to experiment with word2vec or similar techniques, I notice that there lacks a material that comprehensively explains the parameter learning process of word embedding models in details, thus preventing researchers that are non-experts in neural networks from understanding the working mechanism of such models.

Mikolov等人提出的word2vec模型及其应用，在近两年引起了广泛的关注。基于word2vec模型学到的单词向量表示，已经被证明具有语义意义，同时在各种NLP任务中也是有帮助的。越来越多的研究人员，希望使用word2vec或类似的技术，（但在同时）我注意到，目前缺乏一份材料，用于全面、详细地解释 词Embedding模型 的参数学习过程，（这）导致研究者们难以理解这种模型的工作机制，尤其对于不是神经网络专家的研究者。

This note provides detailed derivations and explanations of the parameter update equations of the word2vec models, including the original continuous bag-of-word (CBOW) and skip-gram (SG) models, as well as advanced optimization techniques, including hierarchical softmax and negative sampling. Intuitive interpretations of the gradient equations are also provided alongside mathematical derivations.

本文给出了word2vec模型的参数更新方程的详细推导和解释，包括原始的 连续词袋(CBOW)模型 和 跳跃图(skip-gram, SG)模型，以及先进的优化技术，包括 分层softmax 和负采样。同时提供了梯度方程的直观解释，以及数学推导。

In the appendix, a review on the basics of neuron networks and backpropagation is provided. I also created an interactive demo, wevi, to facilitate the intuitive understanding of the model.

在附录中，回顾了神经网络和反向传播相关基础，同时创建了一个交互式演示——wevi，便于模型的直观理解。

• wevi
  • http://bit.ly/wevi-online
  • https://github.com/ronxin/wevi.git

1. Continuous Bag-of-Word Model

基本结构：

• 输入词：上下文
• 输出词：目标词（中心词）

1.1 上下文为单个词 One-word context

我们从Mikolov等人引入的连续词袋模型(CBOW)的最简单版本开始。
We start from the simplest version of the continuous bag-of-word model (CBOW) introduced in Mikolov et al. (2013a).

Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.

假设每个上下文只考虑一个单词，即给定一个上下文单词后，模型预测一个目标词，就像一个双词模型。
We assume that there is only one word considered per context, which means the model will predict one target word given one context word, which is like a bigram model.

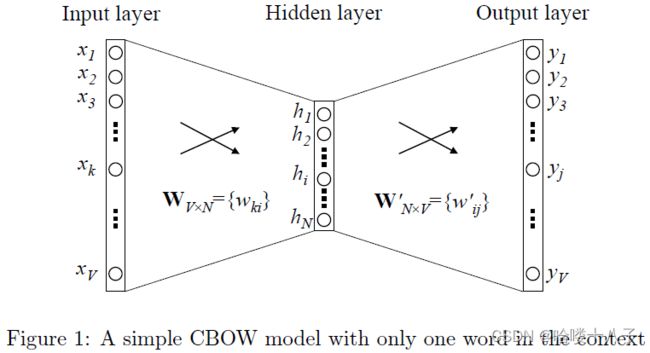
（1）模型结构

• $V$ ：输入层维度，单词总数量，单词one-hot编码维度
• $N$ ：隐藏层维度，单词Embedding后表示向量的维度
• $W$ ：$V\times N$矩阵（$V>>N$），表示输入层到隐藏层之间的全连接关系。
  • 输入矩阵，高且窄
  • 可视作查询词作为中心词时的Embedding查询表
• $W^{\prime }$ ：$N\times V$矩阵（$N<<V$），表示隐藏层到输出层之间的全连接关系。
  • 输出矩阵，矮且宽
  • 可视作查询词作为上下文时的Embedding查询表

PS: $W^{\prime }$并不是$W$的转置

（2）输入层 -> 隐藏层

对于第k个词，编码为ont-hot向量$x$，即$x$中第k个元素为1，其余元素为0。将其作为模型输入：

$$h=W^{T}x=W_{(k,\cdot )}^T=W_{(k,\cdot )}^T:=v_{w_I}^T\text{\hspace{1em}(1)}$$

即$W$ 可作为（一种）word2vec查询表（Look-Up-Table）：第k个单词（输入词$w_I$）的Embedding向量，就是矩阵$W$的第k行（再转置）$v_{w_I}^T$。

其中，$v_{w_I}^T$被称为输入向量；可视作输入词作为中心词时候的Embedding。

$x$右乘$W^T$，即对$W^T$列变换，由于$x$为one-hot编码（假设$x_k=1$），即取$W^T$某一列（第k列），等同于取$W$某一行（第k行）。

（3）隐藏层 -> 输出层

对于输出层的第j个节点，输出的是一个分数值$u_j$：

$$u_j={W_{(:,j)}^{\prime }}^{T}h=:{v_{w_j}^{\prime }}^{T}h\text{\hspace{1em}(2)}$$

其中$v_{w_j}^{\prime }$为$W^{\prime }$的第j列，被称为输出向量；可视作输入词作为上下文时候的Embedding。

分数值$u_j$表示输入词为$w_I$时，其上下文为单词$w_j$的分值，不具有概率意义，即和不为一：

$$\sum _{j=1}^N{u}_j\ne 1$$

因此，为使得模型输出具有概率意义，需要添加softmax函数，获得条件概率分布：

$$prob(w_j|w_I)=\frac{exp(u_j)}{{\sum }_{l=1}^{V}exp(u_l)}:=y_j\text{\hspace{1em}(3)}$$

相当于对输出层使用softmax激活函数。上面输入层到隐藏层相当于没有激活函数，为线性关系。

（4）模型意义

整合上面公式，得到条件概率分布：

$$prob(w_j|w_I)=\frac{exp({v_{w_j}^{\prime }}^T{v}_{w_I})}{{\sum }_{l=1}^{V}exp({v_{w_l}^{\prime }}^T{v}_{w_I})}=y_j\text{\hspace{1em}(4)}$$

可理解为，word2vec模型维护了两套向量表示，分别为：

• 输入向量 —— $v_{w_I}^T$，输入词$w_I$的一种向量表示，来源于$W$的行向量；
• 输出向量 —— $v_{w_j}^{\prime }$，输出词$w_j$的一种向量表示，来源于$W^{\prime }$的列向量；

从输入词到输出词的条件概率分布，被建模为：输入词的输入向量，与输出词的输出向量，两者之间计算内积，再softmax归一化。其中内积起到一种相似性度量的作用。

PS：可以类比Transformer的Multi-Head Attention中的Scaled Dot-Product Attention，每个单词拥有三套表示：Query, Key和Value.

（5）更新方程：隐藏层 -> 输出层

后面开始推导上述模型的参数更新方程。尽管实际的计算过程并不是按照本节的推导进行的，或者说本节的推导并不实用（具体原因后面会解释，见第3节，通过一些trick或近似，使得模型求解更加实用），但是依然想通过微分推导，获得对最原始模型（未使用trick）的直观理解。

根据Eq(5-7)，

$$E=-log[p(w_O|w_I)]=log\sum _{l=1}^{V}exp(u_l)-u_{j\ast }$$

关于$u_j$，对$E$的第1项求导，正好是$y_j$（参照Eq3中$y_j$的定义）；对其第2项求导，是$j=j\ast$的示性函数，于是有Eq8.

Eq9中第二项，参照Eq2中$u_j$的定义和Eq1中$v_{w_j}^{\prime }$的定义.

于是，基于随机梯度下降，得到 隐藏层 -> 输出层的权重$w_{ij}^{\prime }$的更新公式Eq10，或表示为向量的形式，即Eq11.

Eq11中，所有词的输出向量都需要更新；对比后面的Eq16，只有输入词的输入向量需要更新。

直观理解

给定一个输入词后，从词表中遍历所有可能的输出词，例如词表中第j个词，检查模型对其概率密度估计$y_j$，并与期望值$t_j$（即ground truch）比较。

• 如果$y_j>t_j$，即估计过高（此处当且仅当$t_j=0$，即第j个词不是输出词的GT），则需要从$v_{w_j}^{\prime }$中减去一定比例（学习率）的$h$，让输出词$w_j$的输出向量表示 $v_{w_j}^{\prime }$，远离输入词$w_I$的输入向量表示$v_{w_I}$；
• 如果$y_j<t_j$，即估计过低（此处当且仅当$t_j=1$，即第j个词正好是输出词GT），则需要从$v_{w_j}^{\prime }$中加上一定比例（学习率）的$h$，让输出词$w_j$的输出向量表示 $v_{w_j}^{\prime }$，靠近输入词$w_I$的输入向量表示$v_{w_I}$；
• 如果两者差不多，变动也相应很小。

再次指出，输入向量表示$v_w$和输入向量表示$v_w^{\prime }$，是同一单词$w$的两种不同表示方式。

（6）更新方程：输入层 -> 隐藏层

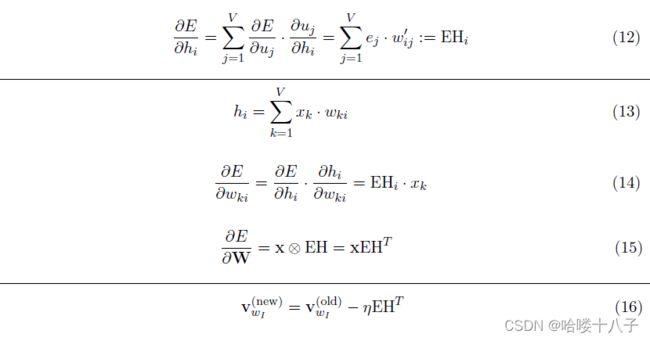
得到$E$关于$W^{\prime }$的更新公式之后，根据链式法则，后面继续推导$E$关于$W$的更新公式。

Eq12得到$E$关于隐层节点$h_i$的偏导，是预测误差$e_j=y_j-t_j$根据$w_{ij}^{\prime }$加权求和后的结果，简记为$E{H}_i$.

$E$关于隐层所有节点$h$的偏导，可简记为$EH$，是一个N维（列）向量（对应N个隐层节点）。

Eq13为Eq1的另一种表示，便于Eq14的推导表示。

Eq14中，下角标k对应第k个输入词，i对应第i个隐层单元。Eq14可以表示为张量积的形式，得到Eq15.

Eq15中，$\frac{\partial E}{\partial W}$为V行N列，x为V行1列，EH为N行1列。

考虑到one-hot向量x的稀疏性（例如$x_k=1$，即$w_I=W_k$），$\frac{\partial E}{\partial W}$ 中只有一行（第k行）是非零的。

x左乘$E{H}^T$ 即对 $E{H}^T$ 行变换，取其一行，而$E{H}^T$也只有一行。即创建一个V行N列的零矩阵，再将$E{H}^T$复制到其第k行。

因此，$W$中仅有一行会被更新到，即第k行，即仅输入词$w_I$对应的那一行会更新；更新方式为向负梯度方向移动，步长为一定比例（学习率）的 $x_k\cdot E{H}^T=E{H}^T$。于是有Eq16。

除了输入词$w_I$之外，其他词$w\ne w_I$的输入向量$v_w$不作更新。

对比前面的Eq11，所有词的输出向量都需要更新。

直观理解

直观的，向量$EH$是词汇表中所有单词输出向量的加权和，权重系数为预测误差$e_j=y_j-t_j$，于是Eq16可以被理解为，将词汇表中每个词的输出向量，按照一定比例，叠加到输入词的输入向量上。

• 如果词$w_j$是输出词的概率被高估，即$y_j>t_j\Rightarrow e_j>0$，输入词$w_I$的输入向量将趋向于远离词$w_j$的输出向量；
• 如果词$w_j$是输出词的概率被低估，即$y_j<t_j\Rightarrow e_j<0$：输入词$w_I$的输入向量将趋向于靠近词$w_j$的输出向量；
• 如果估计的差不多，即$y_j\approx t_j$：输入词$w_I$的输入向量变化很少，所受影响不大；
• 对于某个词$w_j$，其估计误差$e_j$越大，这个词对于上述输入词$w_I$的输入向量的叠加效果，将起到越大的影响；

当我们使用训练语料库，生成 上下文-目标词 对，迭代更新模型参数时，（上面提到的）向量之间的影响会逐渐累积。
As we iteratively update the model parameters by going through context-target word pairs generated from a training corpus, the effects on the vectors will accumulate.

可以想象，某个单词w的输出向量，被其 共现邻居 的输入向量前后拖动，就像有一条绳子一样，连接在单词w和它的相邻词的表示向量中间。
We can imagine that the output vector of a word w is dragged" back-and-forth by the input vectors of w’s co-occurring neighbors, as if there are physical strings between the vector of w and the vectors of its neighbors.

类似地，输入向量也可以被认为是被许多输出向量拖动的。
Similarly, an input vector can also be considered as being dragged by many output vectors.

这种解释可以让我们想起 重力 或者 受力分析图。
This interpretation can remind us of gravity, or force-directed graph layout.

每条虚拟绳子的平衡长度，与关联词对之间的共现强度有关，也与学习率有关。

The equilibrium length of each imaginary string is related to the strength of cooccurrence between the associated pair of words, as well as the learning rate.

经过多次迭代，输入向量和输出向量之间的相对位置，最终将达到稳定。
After many iterations, the relative positions of the input and output vectors will eventually stabilize.

1.2 上下文为多个词 Multi-word context

CBOW模型：多个输入词，如Fig2。

隐层单元：不再是直接从输入词的输入向量中复制（参照Eq1中，ont-hot编码的x右乘矩阵$W$），而是对C个输入词的输入向量计算平均值，于是得到Eq(17-18)。

损失函数：Eq21，与Eq7基本相同。Eq21对Eq7中的$u_j$项进行了展开，便于说明隐层单元$h$的计算存在区别。

更新方程：

• Eq22: 隐藏层 -> 输出层，和Eq11保持一致。输出矩阵$W^{\prime }$的每一个元素都要更新。
• Eq23：输入层 -> 隐藏层，和Eq16相似，区别是需要将梯度平均分配到C个输入词的输入向量上。

2. Skip-Gram Model

和CBOW相反，基本结构：

• 输入词：目标词（中心词）
• 输出词：上下文

（1）模型结构

（2）输入层 -> 隐藏层

Eq24: 和CBOW相同，对比Eq1；

（3）隐藏层 -> 输出层

Eq25: C个多项式分布。和CBOW相似，对比Eq3；
Eq26: Softmax之前的输出节点（分值），对比CBOW的Eq2;

（4）损失函数E

Eq29: 可视作按照Eq7对多个输出词$w_c$分别计算损失$E_c$，再累加求和，对比CBOW的Eq7（单词上下文）和Eq21（多词上下文）；
Eq30：由于Eq29中最终是求和关系，于是$\frac{\partial E}{\partial u_{c,j}}=\frac{\partial E_c}{\partial u_{c,j}}$，与CBOW的Eq8相同。
Eq31: 定义V维向量$EI$，作为 c个输出词上的总误差，便于后续表示；

便于理解的，Skip-Gram中的$E{I}_j$，对应CBOW中的$e_j$；

相当于Skip-Gram的每个输出节点（例如第j个节点），有C个输出误差$e_{c,j}$，$E{H}_j$对其无差别求和，从C维向量压缩到了1维标量；

（5）更新方程：隐藏层 -> 输出层

Eq(32-34)，依次类比CBOW的Eq(9-11)；其中Eq11(单词上下文)和Eq22(多词上下文)基本一致。

便于理解的，Skip-Gram中的$E{I}_j$，对应CBOW中的$e_j$；

（6）更新方程：输入层 -> 隐藏层

Eq35，类比CBOW的Eq(12-16)的推导过程;
Eq36，类比CBOE的Eq12中对$E{H}_i$的定义。

便于理解的，Skip-Gram中的$E{I}_j$，对应CBOW中的$e_j$；

3 Optimizing Computational Effciency

到目前为止，我们讨论的模型(“bigram”模型、CBOW和skip-gram)都是原始形式，没有应用任何优化技巧，来提高训练效率。
So far the models we have discussed (“bigram” model, CBOW and skip-gram) are both in their original forms, without any effciency optimization tricks being applied.

对于所有这些模型，词汇表中的每个单词都有两个向量表示：输入向量$v_w$和输出向量$v_w$。
For all these models, there exist two vector representations for each word in the vocabulary: the input vector $v_w$, and the output vector $v_w$ .

学习输入向量很方便，但是学习输出向量（的代价）是非常昂贵的。
**Learning the input vectors is cheap; but learning the output vectors is very expensive. **

从更新方程(22)和(33/34)，我们可以发现,为了更新$v_w^{\prime }$,对于每个训练实例,我们必须遍历词汇表中的每个单词$w_j$，计算净输入$u_j$（打分分值），概率预测值$y_j$（或者$y_{c,j}$， 对于skip-gram），其预测误差$e_j$（或者$E{I}_j$，对于skip-gram)，最后利用其预测误差，更新其输出向量$v_j^{\prime }$。

From the update equations (22) and (33), we can find that, in order to update $v_w^{\prime }$ , for each training instance, we have to iterate through every word $w_j$ in the vocabulary, compute their net input $u_j$ , probability prediction $y_j$ (or $y_{c,j}$ for skip-gram), their prediction error $e_j$ (or $E{I}_j$ for skip-gram), and finally use their prediction error to update their output vector $v_j^{\prime }$.

为每个训练实例的所有单词，进行这样的计算是非常昂贵的，导致其很难适用于 大型词汇表 或 大型训练语料库 的情况。
Doing such computations for all words for every training instance is very expensive, making it impractical to scale up to large vocabularies or large training corpora.

为了解决这个问题，直觉上，对于每个训练实例，应该限制必须更新的输出向量的数量。
To solve this problem, an intuition is to limit the number of output vectors that must be updated per training instance.

为了实现这一目标，一种优雅的方法是分层softmax；另一种方法是通过采样，这将在下一节中讨论。
One elegant approach to achieving this is hierarchical softmax; another approach is through sampling, which will be discussed in the next section.

这两种技巧，都只优化了输出向量更新的计算方式。在我们的推导过程中，我们关心三个值:
Both tricks optimize only the computation of the updates for output vectors. In our derivations, we care about three values:

1. $E$ ： 新的目标方程（损失函数）—— the new objective function;
2. $\frac{\partial E}{\partial v_w^{\prime }}$ ： 输出向量的新的更新方程 ——the new update equation for the output vectors; and
3. $\frac{\partial E}{\partial h}$ ：预测误差的加权和（参照Eq12），用于（将梯度）反向传播更新输入向量——
   the weighted sum of predictions errors to be backpropagated for updating input vectors.

3.1 Hierarchical Softmax（Trick 1，分层softmax）

（1）模型结构

分层Softmax是一种高效的计算softmax的方式(Morin and Bengio, 2005; Mnih and Hinton, 2009).

Mnih, A. and Hinton, G. E. (2009). A scalable hierarchical distributed language model.
Morin, F. and Bengio, Y. (2005). Hierarchical probabilistic neural network language model.

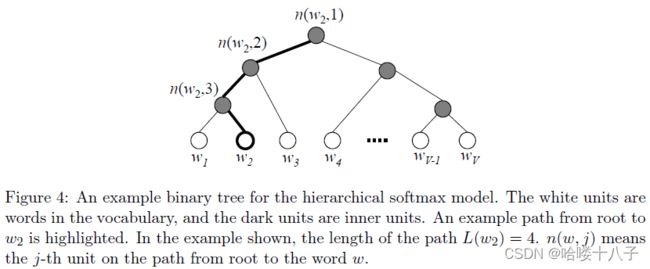
• 用二叉树来示词汇表中的所有单词；
• 每个单词一定是树的叶节点，共V个单词（即V个叶节点）；
• 内部点共V - 1个；
• 对于每一个叶节点，存在唯一一条从根节点到该叶节点的路径，这条路径用来估计叶节点对应单词（为输出词）的概率。

分层softmax模型中，并没有为每个单词维护一个输出向量，而是为每个内节点维护一个输出向量$v_{n(w,j)}^{\prime }$

便于理解的，借助树的结构，将每个单词建模为不同尺度的表示的逐级叠加，粗粒度的表示（靠近根节点）被多个单词共用。

输出词的概率分布被建模为Eq37：

其中，

• $L(w)$：【标量】从单词w对应的叶节点，到根节点的路径长度，例如Fig4中$L(w_2)=4$
• $n(w,j)$：【节点】从根节点，到单词w对应的叶节点，这条路径上的第j个节点（路径唯一）；
• $ch(n)$：【节点】节点$n$的左孩子节点；
• $v_{n(w,j)}^{\prime }$：【Embedding向量】内节点$n(w,j)$的Embedding表示（输出向量）；
• $h$：隐层节点输出，参照Eq1, Eq13, Eq18
• $[[x]]$：x为真/假的示性函数，真为1，假为-1，；参照Eq38;

（2）模型理解

例如，想要计算输出词是$w_2$的概率分布，于是从根节点开始，向叶节点方向进行随机游走（以某种概率策略）。对于每一个内部节点，有两种选择：

• 移动向左孩子节点，对应概率为Eq39;
• 移动向右孩子节点，对应概率为Eq40;

PS：不是所有的二叉树，都能保证每个内节点都有两个子节点，但霍夫曼二叉树（binary Huffman tree）能够保证；
理论上，所有类型的二叉树都能用于分层Softmax，但word2vec为了快速训练，还是选用了霍夫曼二叉树（binary Huffman tree）。

参照Fig4，最终能够到达$w_2$对应的叶节点的概率为：Eq(41, 42)；可作为Eq37的一个示例。

同时不难证明，所有词的概率之和为1，即Eq43.

实际上，树的结构，实现了概率“1”的多级拆分，但总量保持不变。

（3）损失函数

以CBOW模型为例，对于Skip-Gram只需简单修改。

为便于表示，对符号进行简化：Eq44, Eq45
对于一个训练实例，损失函数：Eq46.（不难理解，参考Eq7, Eq19, Eq27）

（4）梯度更新

推导不难理解。

Eq51中，$\sigma ({v_j^{\prime }}^T)-t_j$可视作内节点$n(w,j)$上的预测误差。

训练过程可理解为，从树结构的不同层次上，训练内节点的输出向量，使之逐渐拥有判断向左（孩子节点）还是向右（孩子节点）移动的能力。

对于Skip-Gram，需要稍作修改：将C个单词的损失（Eq46）和梯度（Eq50）进行叠加，参考Eq29, Eq32.

梯度反向传播：

基于更新方程，可以看到分层softmax（第一个trick）的改进和优势：

• 对于每一个训练样例（中心词），计算复杂度从$O(V)$降低到了$O(log(V))$，可以显著加快训练速度；
• 同时，模型参数却基本保持一致，输出向量个数仅从V减少到了V-1（即模型容量，或拟合复杂函数的能力，基本没有降低）；

个人理解：分层softmax采用分而治之的思想。对于每个内节点$n$，以其输出向量$v_n^{\prime }$为法线的超平面，将Embedding所在的N维空间切分为两个子空间。从根节点到某叶子结点的唯一一条路径上，有L个节点，表示对整个输出向量空间依次进行L次切分，相当于通过二分法逐步完善概率空间。

一个疑问：类比决策树，基于多种“纯度”指标，对子节点进行分裂，从而同一子树上的节点，具有一定相似性。但对于本文 分层softmax 中使用的二叉树，单词和叶节点的对应关系，是否在训练过程中会被调整和优化？或者说，同一子树上的节点对应的单词，是否具有相似性？相似性是如何保证的？可能需要再看下参考文献、霍夫曼二叉树等相关资料。

3.2 Negative Sampling（Trick 2，负采样）

相比于分层softmax，负采样思想的对问题的处理，更加简单直接：

既然问题的难点是，每一轮迭代中，有太多输出向量需要更新，那么就对之简化，只更新一部分（一个采样）就可以了。

显然，真正的输出词（Ground Truth, 正样本）肯定需要被采样到，并被更新到；于是，只需要再采样少量的负样本就可以了。

（负样本）采样的概率分布，可以被根据经验，随机选取，称作噪声分布，记作$P_n(w)$。

（1）损失函数

word2vec中，相比于“使用 一种负采样方式，使之完美地契合（训练样本的）后验多项式分布”的方式，作者提出使用Eq55中简化的训练目标，同样可以产生高质量的词表示向量.

其中，第1项对应正样本，第2项对应负样本的采样。

对比Eq21，第1项相同，均为正样本；第2项对应全量的样本（自然包括全量的负样本）。

（2）梯度更新

基于Eq55中简化的优化目标，可推导得到相应的梯度和更新方程 Eq(56-61)：

其中，对更新方程Eq59的直观理解，和Eq11相同。

（3）优势

1. 每轮迭代中，仅采样出少量的负样本进行更新，而未被采样到的负样本则忽略不更新，这减少了大量计算量。
2. 相比于分层softmax，简单粗暴，且效果不差。