力扣刷题日常——树
刷了剑指offer入门以及突击版,总结一下有关于树的题,主要还是深度优先搜索和广度优先搜索。
1. 广度优先搜索(BFS)
主要是结合队列完成
- 剑指 Offer II 043. 往完全二叉树添加节点
- 剑指 Offer II 044. 二叉树每层的最大值
- 剑指 Offer II 045. 二叉树最底层最左边的值
- 剑指 Offer II 046. 二叉树的右侧视图
1.1 二叉树的BFS框架
框架一
//只对这棵树有操作(一次)
Queue<TreeNode> queue = new Queue<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode t = queue.poll();
if(t.left!=null) queue.offer(t.left);//或者其他操作
if(t.right!=null) queue.offer(t.right);
}
框架二
//对每一层都有操作
Queue<TreeNode> queue = new Queue<>();
queue.offer(root);
while(!queue.isEmpty()){
int len = queue.size();
for(int i=0;i<len;i++){
TreeNode t = queue.poll();
if(t.left!=null) queue.offer(t.left);//或者其他操作
if(t.right!=null) queue.offer(t.right);
}
}
1.2 往完全二叉树添加节点
题目描述
完全二叉树是每一层(除最后一层外)都是完全填充(即,节点数达到最大,第 n 层有 2n-1 个节点)的,并且所有的节点都尽可能地集中在左侧。
设计一个用完全二叉树初始化的数据结构 CBTInserter,它支持以下几种操作:
- CBTInserter(TreeNode root) 使用根节点为 root 的给定树初始化该数据结构
- CBTInserter.insert(int v) 向树中插入一个新节点,节点类型为 TreeNode,值为 v
- 使树保持完全二叉树的状态,并返回插入的新节点的父节点的值;
- CBTInserter.get_root() 将返回树的根节点。
结题思路
使用层序遍历寻找新节点插入位置,当遍历到 “不完整的节点” 就找到了新节点插入的节点位置,“不完整的节点” 位于队列的头部。
代码
public class CBTInserteroff043 {
TreeNode root;
Queue<TreeNode> q;
public CBTInserteroff043(TreeNode root) {
this.root = root;
q = new LinkedList<>();
q.offer(root);
while(q.peek().left!=null&&q.peek().right!=null){//保证队列第一个节点就是不完整节点
q.offer(q.peek().left);
q.offer(q.peek().right);
q.poll();
}
}
public int insert(int v) {
TreeNode front = q.peek();
TreeNode node = new TreeNode(v);
if(front.left==null){
front.left = node;
}
else{
front.right = node;//补上右边就完整了,把完整节点弹出去,左右节点加进来
q.offer(front.left);
q.offer(node);
q.poll();
}
return front.val;
}
public TreeNode get_root() {
return root;
}
}
1.3 二叉树每层的最大值
题目描述
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
代码
class Solution {
public List<Integer> largestValues(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
List<Integer> res = new LinkedList<>();//存贮每一层最大值
int nums = Integer.MIN_VALUE;
if(root!=null)
q.offer(root);
while (!q.isEmpty()){
int l = q.size();
for(int i=0;i<l;i++){
TreeNode tmp = q.poll();
nums = Math.max(nums,tmp.val);
if(tmp.left!=null) q.offer(tmp.left);
if(tmp.right!=null) q.offer(tmp.right);
}
res.add(nums);
nums = Integer.MIN_VALUE;
}
return res;
}
}
2. 深度优先搜索(DFS)
递归思想:
- 剑指 Offer II 047. 二叉树剪枝 (DFS)
- 剑指 Offer II 048. 序列化与反序列化二叉树(DFS)
- 剑指 Offer II 049. 从根节点到叶节点的路径数字之和(DFS+前缀和)
- 剑指 Offer II 050. 向下的路径节点之和 (DFS+前缀和)
- 剑指 Offer II 051. 节点之和最大的路径(DFS)
- 剑指 Offer II 052. 展平二叉搜索树 (DFS+PreNode)
- 剑指 Offer II 053. 二叉搜索树中的中序后继 (DFS)
- 剑指 Offer II 054. 所有大于等于节点的值之和 (DFS)
- 剑指 Offer II 055. 二叉搜索树迭代器 (DFS)
- 剑指 Offer II 056. 二叉搜索树中两个节点之和(DFS+HashSet)
2.1 二叉树的DFS框架
/* 二叉树遍历框架 */
void traverse(TreeNode root) {
// 前序遍历
traverse(root.left)
// 中序遍历
traverse(root.right)
// 后序遍历
}
2.2 序列化与反序列化二叉树 (DFS)
题目描述
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
 二叉树的序列化本质上是对其值进行编码,更重要的是对其结构进行编码。可以遍历树来完成上述任务。可以使用先序遍历,遇到空子树的时候序列化成 None,否则继续递归序列化。对于反序列化根据 , 把原先的序列分割开来得到先序遍历的元素列表,然后从左向右遍历这个序列:如果当前的元素为 None,则当前为空树。否则先解析这棵树的左子树,再解析它的右子树。
二叉树的序列化本质上是对其值进行编码,更重要的是对其结构进行编码。可以遍历树来完成上述任务。可以使用先序遍历,遇到空子树的时候序列化成 None,否则继续递归序列化。对于反序列化根据 , 把原先的序列分割开来得到先序遍历的元素列表,然后从左向右遍历这个序列:如果当前的元素为 None,则当前为空树。否则先解析这棵树的左子树,再解析它的右子树。
代码
public class Codecoff048 {
// Encodes a tree to a single string.
List<String> res = new LinkedList<>();
public String serialize(TreeNode root) {
if(root==null)
return "null";
res.add(String.valueOf(root.val));
serialize(root.left);
serialize(root.right);
return String.join(",",res);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
Queue<String> q = new LinkedList<>(Arrays.asList(data.split(",")));
return dfs(q);
}
public TreeNode dfs(Queue<String> queue){
if(queue.size()==0)
return null;
String val = queue.poll();
if(val.equals("null")){
return null;
}
TreeNode root = new TreeNode(Integer.parseInt(val));
root.left = dfs(queue);
root.right = dfs(queue);
return root;
}
}
}
2.3 从根节点到叶节点的路径数字之和(DFS+前缀和)
题目描述
给定一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。计算从根节点到叶节点生成的 所有数字之和 。叶节点 是指没有子节点的节点。
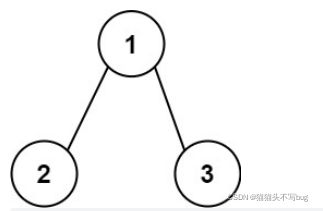
输入
root = [1,2,3]
输出
25
解释
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
解题思路
从根节点开始,遍历每个节点,如果遇到叶子节点,则将叶子节点对应的数字加到数字之和。如果当前节点不是叶子节点,则计算其子节点对应的数字,然后对子节点递归遍历。所以需要一个变量来记录前面的数字之和。
代码
public class sumNumbersoff049 {
// int sum = 0;
public int sumNumbers(TreeNode root){
//dfs
return dfs(root,0);
}
public int dfs(TreeNode root,int presum){
if(root==null){
return 0;
}
int sum = presum*10+root.val;
if(root.left==null&&root.right==null){//到达叶子节点
return sum;
}
else{
return dfs(root.left,sum)+dfs(root.right,sum);
}
}
}
相同类型的还有:剑指 Offer II 054. 所有大于等于节点的值之和
2.4 二叉搜索树中的中序后继(DFS+PreNode)
题目描述
给定一棵二叉搜索树和其中的一个节点 p ,找到该节点在树中的中序后继。如果节点没有中序后继,请返回 null 。
节点 p 的后继是值比 p.val 大的节点中键值最小的节点,即按中序遍历的顺序节点 p 的下一个节点。
 解题思路
解题思路
对二叉树进行中序遍历,如果节点p的值大于当前节点那么继续遍历。如果节点p的值小于当前节点,那么p的中继后序就是当前节点。
代码
public class inorderSuccessoroff053 {
TreeNode pre = null,res = null;
int flag = 0;
public TreeNode inorderSuccessor(TreeNode root,TreeNode p){
dfs(root,p);
return res;
}
public void dfs(TreeNode root,TreeNode p){
if(root==null)
return ;
dfs(root.left,p);
if(root.val>p.val) {
flag++;
if(flag==1)//找第一个比p大的数
res = root;
}
// if(pre==p) res = root;
// pre = root;
dfs(root.right,p);
}
}