一周刷爆LeetCode,直击BTAJ等一线大厂必问算法面试题真题详解 【第二弹】
目录
6、折半查找
6.1 关于折半查找及其思想
6.2 普通实现
6.3 递归实现
7、master公式
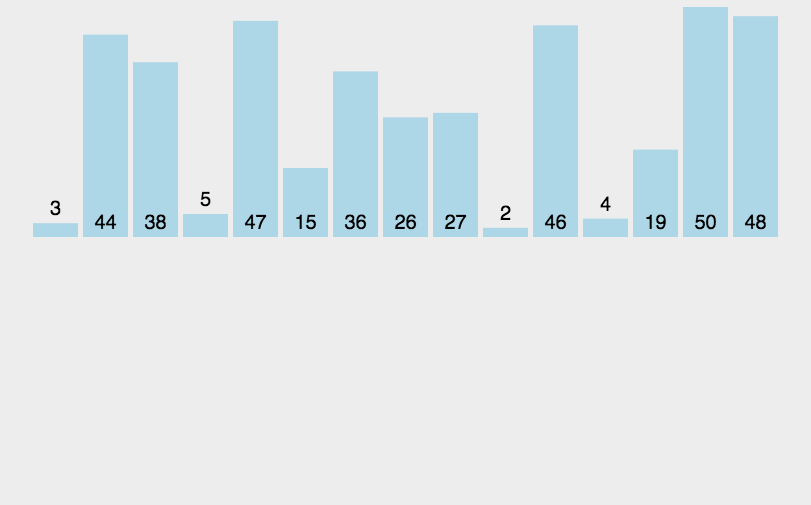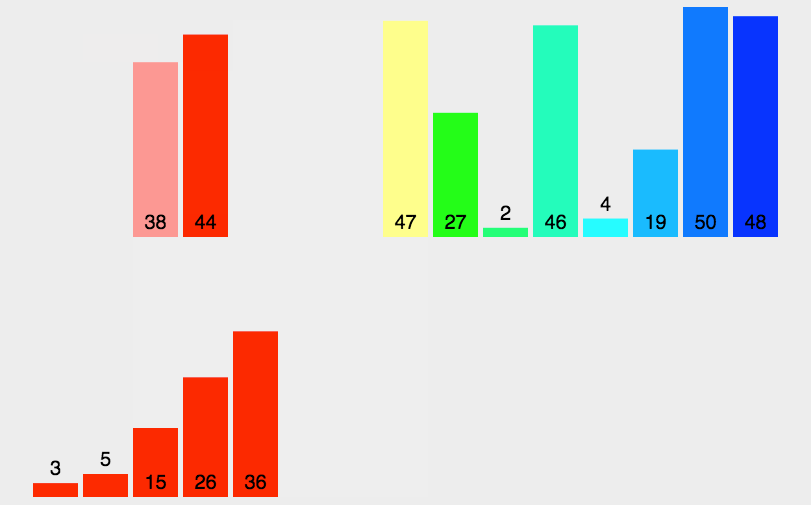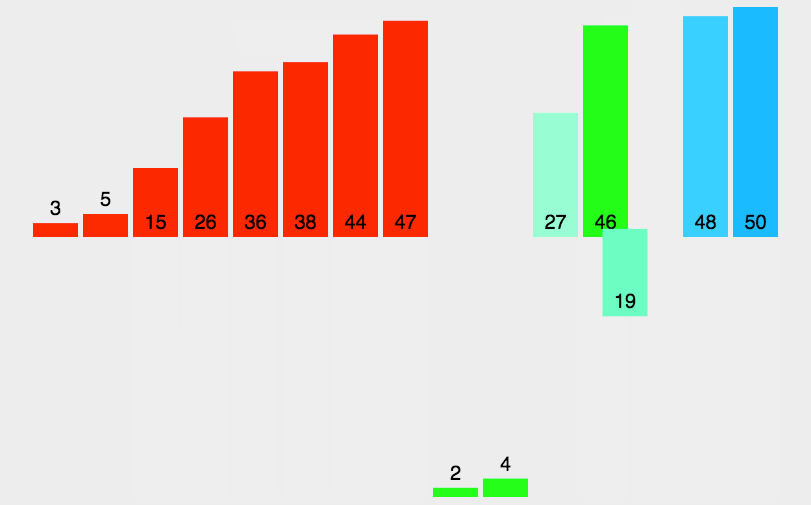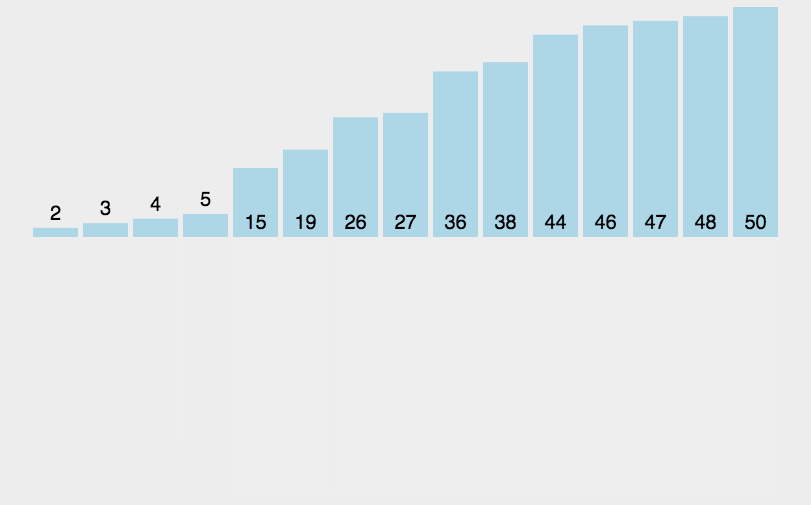
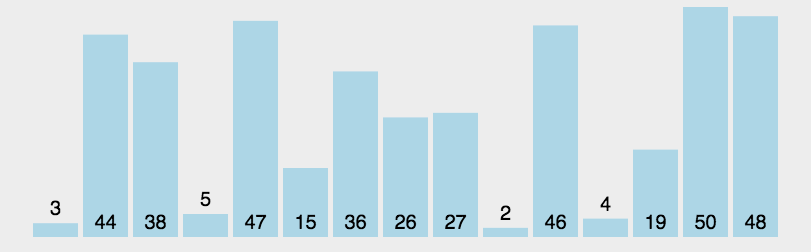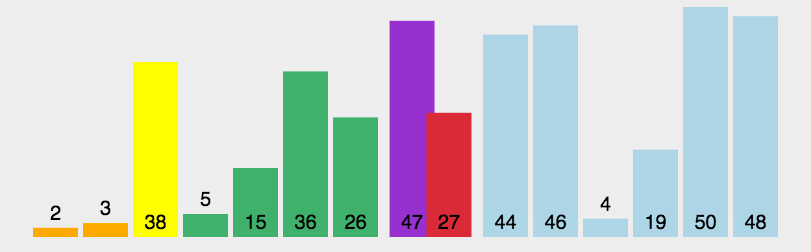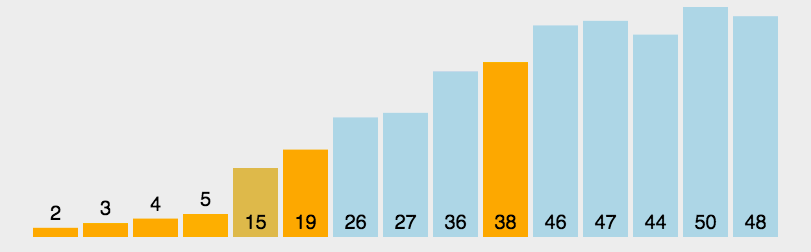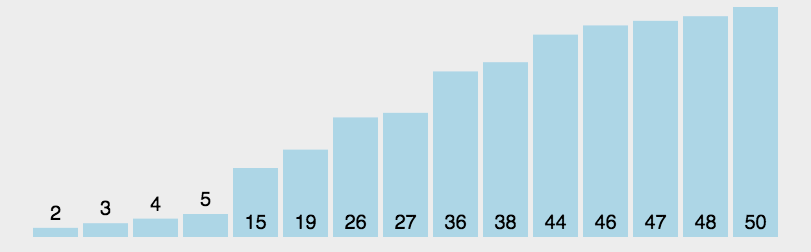
8、归并排序
8.1 归并排序
8.2 315. 计算右侧小于当前元素的个数
9、快速排序
9.1 荷兰国旗问题
9.2 快速排序
6、折半查找
6.1 关于折半查找及其思想
如果从文件中读取的数据记录的关键字是有序排列的(递增的或是递减的),则可以用一种更有效率的查找方法来查找文件中的记录,这就是折半查找法,又称为二分搜索。
折半查找的基本思想:减少查找序列的长度,分而治之地进行关键字的查找。他的查找过程是:先确定待查找记录的所在的范围,然后逐渐缩小查找的范围,直至找到该记录为止(也可能查找失败)。例如文件记录的关键字序列为:
(1,3,5,7,9,11,13,17,21,28,32)
该序列包含11个元素,而且关键字单调递增。现在想查找关键字key为28的记录。如果应用顺序查找法进行查找,需要将28之前的所有关键字与key进行比较,共需10次,如果用折半查找可以这样做: 设指针low和high分别指向关键字序列的上界和下界,即low=0,high=10。指针mid指向序列的中间位置,即mid=[(low+high)/2]=5。在这里low指向关键字1,high指向关键字32,mid指向关键字11。
(1,3,5,7,9,11,13,17,21,28,32)
↑ ↑ ↑
low mid high
(1)首先将mid所指向的元素与key进行比较,因为key=28,大于11,这就是说明待查找的关键字一定位于mid和high之间。这是因为原关键字序列是有序递增的。因此下面的查找工作只需在[mid+1,high]中进行。于是指针low指向mid+1的位置,即low=6,也就是指向关键字13,并将mid调整到指向关键字21,即mid=8。
(1,3,5,7,9,11,13,17,21,28,32)
↑ ↑ ↑
low mid high
(2)再将mid所指向的元素与key进行比较,因为key=28,大于21,说明待查找的关键字一定位于mid和high之间。所以下面的查找工作仍然只需在[mid+1,high]中进行。于是指针low指向mid+1的位置,即low=9,也就是指向关键字28,并将mid调整到指向关键字28,即mid=9。high保持不变。
(1,3,5,7,9,11,13,17,21,28,32)
↑ ↑
mid high
low
(3)接下来仍然将mid所指元素与key进行比较,比较相等,查找成功,返回mid的值9。 假设要查找的关键字key为29,那么上述的查找还要继继续下去。由于当前mid所指的元素是28,小于29,因此下面的查找工作仍然只需在[mid+1,high]中进行。将指针low指向mid+1的位置,并调整指针mid的位置。这时指针mid,low与high三者重合,都指向关键字32,它们的值都为10。
(1,3,5,7,9,11,13,17,21,28,32)
↑
high mid low
再将mid所指的元素与key进行比较,因为key=29,小于32,说明待查找的关键字一定位于low和mid之间。所以下面的查找工作仍然只需在[low,mid-1]中进行。于是令指针high指向mid-1的位置,即high=9,也就是指向关键字28.这是指针high小于指针low,这表明本次查找失败。
6.2 普通实现
public static void BinarySearch(int[] array,int x) {
int high = array.length-1;
int low = 0;
int mid = -1;
int found = 0;
while (low<=high) {
mid = high + ((low-high)>>2);
//避免因数组长度过长引起超过int范围
//(high+low)/2 = high+(high-low)/2 = high + ((low-high)>>2
if(x == array[mid]){
found = 1;
System.out.println(x+"在数组中出现的位置"+mid);
}
if(x > array[mid]){
low = mid + 1;
break;
}
if(x < array[mid]){
high = mid - 1;
break;
}
}
if(found == 0){
System.out.println("查找失败!");
}
}6.3 递归实现
折半查找处最大值
public static int searchMax(int[] array){
return process(array,0,array.length-1);
}
public static int process(int[] array,int L,int R){
if(L==R){
return array[L];
}
int mid = L + ((R-L)>>2);
int leftMax = process(array,L,mid);
int rightMax = process(array, mid+1,R);
return Math.max(leftMax,rightMax);
}
}上述例子符合master公式的基本形式可利用master公式进行计算时间复杂度,
符合T(N)= 2 * T(N / 2) + o(1)该形式,a=2,b=2,d=0,所以log(b,a) = d,时间复杂度为 0 (N ^ IogN)
母问题的时间复杂度 = 子问题调用的次数 * 子问题的规模(将母问题分成几份进行分析)+ 除去调用过程的其他过程
7、master公式
剖析递归行为和递归行为时间复杂度的估算
用递归方法找一个数组中的最大值,系统上到底是怎么做的?
master公式的使用
T(N)= a*T(N/b)1+0(N^d)
母问题的时间复杂度 = 子问题调用的次数 * 子问题的规模(将母问题分成几份进行分析)+ 除去调用过程的其他过程
1) log(b,a) > d -> 复杂度为 0(N ^ log(b,a))
2) log(b,a) = d -> 复杂度为 0 (N ^ d * IogN)
3) log(b,a) < d -> 复杂度为 0(N ^ d)
补充阅读:www.gocalf.com/blog/algorithm-complexity-and-master-theorem.html
8、归并排序
8.1 归并排序
1)整体就是一个简单递归,左边排好序、右边排好序、让其整体有序
2)让其整体有序的过程里用了排外序方法
3)利用master公式来求解时间复杂度
4)归并排序的实质 时间复杂度0(N*IogN),额外空间复杂度0(N)
public static void process(int[] arr, int L, int R) {
if(L ==R){
return;
}
int mid = L + ((R - L) >> 1);
process(arr, L, mid);
process(arr, mid + 1, R);
merge(arr, L, mid, R);
}
public static void merge(int[] arr, int L, int M, int R) {
int[] help = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++]= arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];//将临时数组的值赋值给原数组,注意是从L开始的
}
}8.2 315. 计算右侧小于当前元素的个数
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量
输入:nums = [5,2,6,1] 输出:[2,1,1,0] 解释: 5 的右侧有 2 个更小的元素 (2 和 1) 2 的右侧仅有 1 个更小的元素 (1) 6 的右侧有 1 个更小的元素 (1) 1 的右侧有 0 个更小的元素
利用归并排序简化思想: 每合并一次就进行一次小于的比较,使得遍历一次就能拿到所有小于当前元素的个数(和)
下面代码是计算左侧小于当前元素的和
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组的小和。
例子:[1,3,4,2,5]1左边比1小的数,没有;
3左边比3小的数,1;
4左边比4小的数,1、3;
2左边比2小的数,1;
5左边比5小的数,1、3、4、2;
所以小和为1+1+3+1+1+3+4+2=16
public static int process(int[] arr, int i, int r) {
if(i==r){
return 0;
}
int mid = i +((r -i)>> 1);
return process(arr, i, mid) + process(arr, mid + 1, r) + merge(arr, i, mid, r);
}
public static int merge(int[] arr, int L, int m, int r) {
int[] help = new int[r -L + 1];//开辟空间
int i =0;
int p1 = L;
int p2=m+ 1;
int res = 0;
while (p1 <= m && p2 <= r){
res+=arr[p1]< arr[p2]?(r-p2+1)*arr[p1]:0;//只要该值大于左边数组,那么该值右边的一定大于
help[i++] = anr[p1] < arr[p2] ? arr[pl++]: arr[p2++];//当两值相等的时候必须先插入右边的,否则无法计算右边数组中到底有多少个大于该数的
}
while (p1<= m){
help[i++] = arr[pl++];
}
while (p2 <= r) {
help[i++] =arr[p2++];
}
for (i = 0;i < help.length;i++) {
arr[L + i] = help[i];//会放到arr数组当中,方便下次递归使用
}
return res;
}9、快速排序
9.1 荷兰国旗问题
问题一
快排1.0版本,一次排一个数
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。要求额外空间复杂度0(1),时间复杂度0(N)
解题思路: 1)[i] <= num, [i] 与 <=区 的下一个数交换,<=区右扩,i++ 2)[i] > num, i++
左侧为 <=区 ,右侧为待定区
问题二(荷兰国旗问题)
快排2.0版本,一次排一堆相同的数
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。要求额外空间复杂度0(1),时间复杂度O(N)
解题思路: 1)[i] < num, [i]和<区下一个交换,<区右移,i++ 2) [i] == num, i++ 3) [i] > num, [i]和>区前一个交换,>区右移,i原地不动(因为交换后还未进行比较)
9.2 快速排序
快速排序也是一种较为基础的排序算法,其效率比冒泡排序算法有大幅提升。因为使用冒泡排序时,一趟只能选出一个最值,有n个元素最多就要执行n - 1趟比较。而使用快速排序时,一次可以将所有元素按大小分成两堆,也就是平均情况下需要logn轮就可以完成排序。
快速排序的思想是:每趟排序时选出一个基准值,然后将所有元素与该基准值比较,并按大小分成左右两堆,然后递归执行该过程,直到所有元素都完成排序。
快速排序的步骤如下:
1)先从数列中取出一个数作为基准数。
2)分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3)再对左右区间重复第二步,直到各区间只有一个数。
在选择基准值的时候,越靠近中间,性能越好;越靠近两边,性能越差。3.0版本 随机选一个数进行划分的目的就是让好情况和差情况都变成概率事件。把每一种情况都列出来,会有每种情况下的时间复杂度,但概率都是1/N。那么所有情况都考虑,时间复杂度就是这种概率模型下的长期期望。
时间复杂度O(N*logN),额外空间复杂度O(logN)都是这么来的。
public static void quickSort(int[] arr) {
if (arr == null || arr.length <2){
return;
}
quickSort(arr, 0, arr.length - 1);
}
// arr[1..r]排好序
public static void quickSort(int[] arr, int L, int R) {
if(L< R){
swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
int[] p = partition(arr, L, R);
quickSort(arr, L, p[0]-1); // < 区
quickSort(arr, p[1]+1, R); // > 区
}
}
//这是一个处理arr[1..r]的函数
//默认以arr[r]做划分,arr[r]->p p
//返回等于区域(左边界,右边界),所以返回一个长度为2的数组res,res[o]res[1]
public static int[] partition(int[] arr, int L, int R) {
int less=L-1;//<区右边界
int more=R;//>区左边界
while(L< more){ // L表示当前数的位置 arr[R] -> 划分值,当当前位置大于等于>区左边界时跳出
if(arr[L]arr[R]){//当前数>划分值
swap(arr, --more, L);
} else {
L++;
}
}
swap(arr, more, R);
return new int[] { less + 1, more };
}