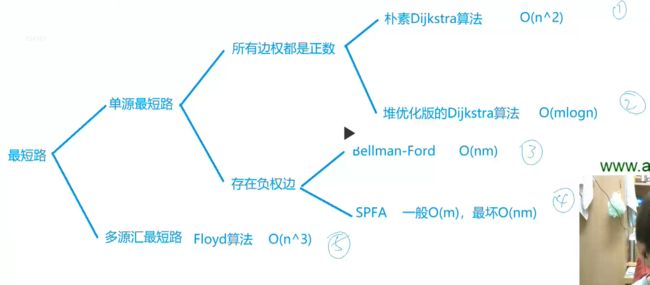
我们之前介绍的求最短路问题,我们通常会考虑到用BFS算法计算,这里我们将这样对于求最短路问题用不同的算法进行分类:
思路介绍:Dijkstra算法的思路究竟是怎么样的,我们这里先介绍一下朴素版Dijkstra算法的思路:
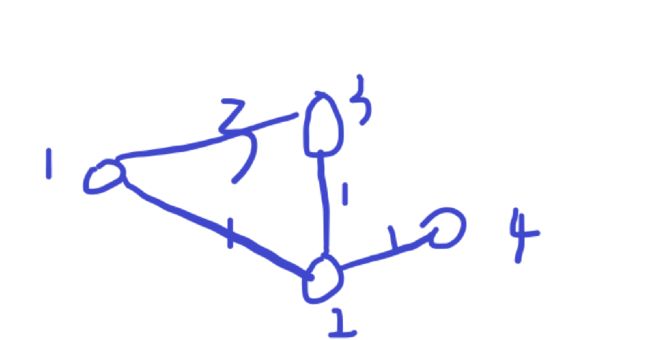
因为我们要去计算的是每个节点到起始点的最短距离,所以我们使用的方法是不断地迭代更新数值,我们会利用一个st数组(state)来表示每个结点的状态,我们保证的是如果st【i】 = true了,那么我们就可以说dist【i】存储的就是从这个点到起始点的最短距离了,所以为了保证每一个节点都能够被保证其最小值,我们需要在外层循环n次,然后在内循环中,我们先去定义一个t,t这个节点指的是目前到起始点最近的点,然后我们从这个点出发去更新他能直接走到的所有的点的位置,但是值得注意的是,我们从当前的点走到的下一个点所得出的dist不一定就是最小的情况,比如下图的情况:
我们可以发现,第一个t是1点,从点1出发能更新到2,3两个点,但是此时的dist[3] =3,很明显不是最小的,所以我们下一个t值是2,从点2开始走,更新点3,所以我们要用到min函数;
代码:
#include
#define maxn 510
using namespace std;
int G[maxn][maxn] , dist[maxn],n,m;
bool st[maxn];
int dijkstra(){
memset(dist , 0x3f , sizeof(dist));
dist[1] = 0;
for (int i = 0; i < n; i ++ ){
int t = -1;
for (int j = 1; j <= n; j ++ ){
if(!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
}
st[t] = true;
for (int j = 1; j <= n; j ++ ){
dist[j] = min(dist[j] , dist[t] + G[t][j]);
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(G,0x3f,sizeof(G));
cin >> n >> m;
while (m -- ){
int x , y , z;
cin >> x >> y >> z;
G[x][y] = min(G[x][y],z);
}
int ans = dijkstra();
cout << ans;
return 0;
}
分析:
·首先,我们解释一下G数组,这是个邻接矩阵,这也是一种常见的存储树和图之间关系的方式,与邻接表不同的是,这个通常用于存储比较稠密的图,二邻接表通常用于存储比较稀疏的图;
·我们发现我们把G数组和dist数组都先初始化为0x3f3f3f3f,这是为了之后我们在更新数值的时候不会更新那些我们无法从当前的节点走到的节点;
因为可以发现,我们用邻接矩阵存储图,我们不能直接的找到他能走到的下一个节点,所以我们是通过一股脑的遍历所有元素来取最小值,我们会发现如果两者之间没有直接的联系,G[t][j] + dist[t] > 0x3f3f3f3f = dist[j];