数字图像基本操作——图像采样、量化、算术运算、点运算实验结果及分析

一、实验目的和要求
1.掌握Anaconda中搭建课程实验环境的方法；
2.掌握读、写图像的基本方法；
3.掌握python语言中图像数据与信息的读取方法；
4.掌握图像基本属性的操作方法；
5.掌握图像的简单运算方法；

二、实验内容
1.使用Anaconda搭建课程实验环境。
2.实现图像模拟采样的代码。
3.实现图像量化的代码。
4.实现图像算术运算的代码。
5.实现图像点运算的代码。

三、实验仪器、设备
Anaconda编程环境、pycharm

四、实验原理
（一）图像采样
定义:采样(Sampling)是指将空间上或时间上连续的图象(模拟图象)变换
成离散采样点(象素)集合的一种操作。
采样是对图像空间坐标的离散化。分为均匀采样和非均匀采样。

图1采样原理

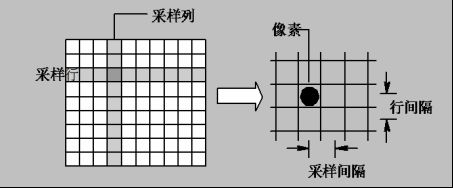
对一幅图像采样时，若每行（即横向）像素为N个，每列（即纵向）像素为M个，则图像大小为M×N个像素，从而f(i,j)构成一个M×N实数矩阵：

把图像分割成像素的方法是多种多样的。即划分的小区域可以是正方形的,
三角形的或六角形的。

（二）图像量化

定义：量化是把采样后所得的各像素灰度值从连续量到离散量的转换称为图
像灰度的量化。

图2量化原理

采样图像的量化方法：均匀量化和非均匀量化。

图3量化实现连续图像到数字图像的转换

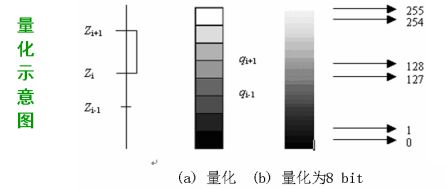
（三）图像算术运算
算术运算也称代数运算，指两幅或两幅以上的输入图像中对应像素的灰度值
做加、减、乘、除等运算，将对应位置像素值的运算结果作为输出图像相应像素
的灰度值。
设输入图像为A(x,y)、B(x,y)，输出图像为C(x,y)，则图像的代数运算有
如下四种形式：
C(x,y)=A(x,y)＋B(x,y)
C(x,y)=A(x,y)－B(x,y)
C(x,y)=A(x,y)×B(x,y)
C(x,y)=A(x,y)÷B(x,y)
（1）加法运算
用来生成叠加图像
C(x,y)=A(x,y)＋B(x,y);
可以得到各种合成图象，也可以用于两幅图像的镶嵌和滤波等。

图4图像的加法运算

（2）减法运算
C(x,y)=A(x,y)-B(x,y);
去除不需要的叠加图像，检测同一场景两幅图像之间的变化。

图5图像的减法运算

（四）图像点运算
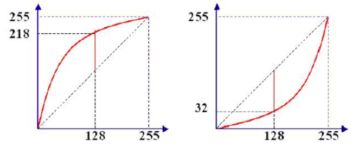
点运算输出图像每个像素的灰度值仅仅取决于输入图像中相对应像素的灰度值。幂次变换属于其中的非线性点运算，图像呈非线性关系。
该运算使图像中具有中间灰度级的像素的灰度发生较大变化，而亮像素和暗像素只作较小变化。

亮度增大 亮度减小 图6图像的非线性点运算

五、实验步骤
（一）使用Anaconda搭建课程实验环境：
（1）下载并安装Anaconda，Anaconda的国内镜像：
Anaconda国内镜像
https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/

（2）更新国内源

• condaconfig--addchannelshttps://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
• condaconfig--addchannelshttps://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main/
• condaconfig--setshow_channel_urlsyes
• pipconfigsetglobal.index-urlhttps://pypi.tuna.tsinghua.edu.cn/simple

• （3）配置虚拟环境
  condacreate–nameDIPpython=3.7
  condaactivateDIP
  （4）安装skimage和opencv及相关插件

• pip installscikit-image
• pip installopencv-python
• pip installmatplotlib

• （5）在pycharm中配置解释器。
  
  

  图1.7 配置解释器

  五、实验结果

  1.实现图像模拟采样的代码。

  # 导入所需要的包
  from skimage import data,io
  from matplotlib import pyplot as plt
  #from matplotlib import pylot as plt
  import numpy as np
  plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
  plt.rcParams['axes.unicode_minus']=False
  
  # 载入测试图像
  image=io.imread('cat.jpg')
  plt.subplot(1,2,1)
  plt.imshow(image)
  plt.title('原始图片')
  
  print(image.shape)  # 显示图像原始大小
  print(type(image))  # 显示图像类型
  ratio = 5  # 设置采样比率
  # 设置采样后的图片大小
  image1 = np.zeros((int(image.shape[0] / ratio), int(image.shape[1] / ratio), image.shape[2]), dtype='int32')
  # 对图像进遍历
  for i in range(image1.shape[0]):
      for j in range(image1.shape[1]):
          for k in range(image1.shape[2]):
              delta = image[i * ratio:(i + 1) * ratio, j * ratio:(j + 1) * ratio, k]  # 获取需要采样的图像块
              image1[i, j, k] = np.mean(delta)  # 计算均值，并存入结果图像
  
  plt.subplot(1,2,2)
  plt.imshow(image1)
  plt.title('采样后')
  plt.savefig('plt.jpg')
  plt.show()
  

  当采样比率为20时，运行结果如下：
  
  

  图12 图像采样图

  当采样比率为5时，运行结果如下：
  

  图13 图像采样图

  2.实现图像量化的代码。

  from skimage import data
  from matplotlib import pyplot as plt
  
  image=io.imread('cat.jpg')#  载入测试图像
  plt.subplot(1,2,1)
  plt.imshow(image)
  plt.title('原始图片')
  radio =128  # 设置量化比率，128—2级，64—4级
  for i in range(image.shape[0]):
      for j in range(image.shape[1]):
          for k in range(image.shape[2]):
              # 对图像中每个像素进行量化
              image[i][j][k] = int(image[i][j][k] / radio) * radio
  plt.subplot(1,2,2)
  plt.imshow(image)
  plt.title('量化后')
  plt.savefig('plt.jpg')
  plt.show()
  

  将256级灰度的彩色图像量化到仅有2级（每个像素所具有的离散灰度级数（不同灰度值的个数））的灰度图像，运行结果如下：
  

  图14 图像量化图

  将256级灰度的彩色图像量化到仅有4级（每个像素所具有的离散灰度级数（不同灰度值的个数））的灰度图像，运行结果如下：
  

  图15 图像量化图

  3.实现图像算术运算的代码。

  from skimage import data,io,color
  from matplotlib import pyplot as plt
  from matplotlib.font_manager import FontProperties
  font_set=FontProperties(fname=r"c:\windows\fonts\simsun.ttc",size=12)
  
  sky=io.imread('starry_sky.jpg')#  载入测试图像
  sky=color.rgb2gray(sky)
  
  cat=io.imread('cat.jpg')#  载入测试图像
  cat=color.rgb2gray(cat)
  
  image_minus = sky - cat
  image_plus = sky + cat
  plt.set_cmap(cmap='gray')
  
  plt.subplot(2, 2, 1)
  plt.title('星空图像', fontproperties=font_set)
  plt.imshow(sky)
  
  plt.subplot(2, 2, 2)
  plt.title('小猫图像', fontproperties=font_set)
  plt.imshow(cat)
  
  plt.subplot(2, 2, 3)
  plt.title('星空加小猫图像', fontproperties=font_set)
  plt.imshow(image_plus)
  
  plt.subplot(2, 2, 4)
  plt.title('星空减小猫图像', fontproperties=font_set)
  plt.imshow(image_minus)
  
  plt.show()
  
  

  运行结果如下：
  

  16 图像算术运算图

  4.实现图像点运算的代码。

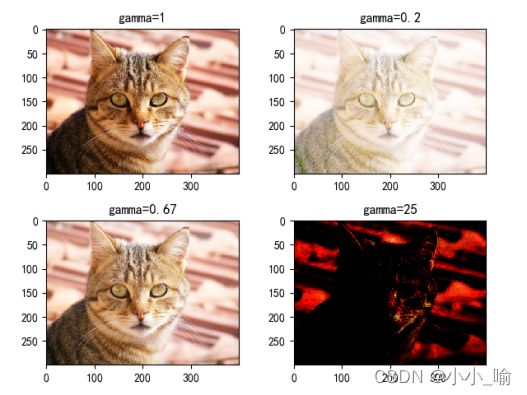
  from skimage import data, io, exposure
  from matplotlib import pyplot as plt
  image=io.imread('cat.jpg')#  载入测试图像
  # 分别计算gamma=0.2,0.67,25时的图像
  image_1 = exposure.adjust_gamma(image, 0.2)
  image_2 = exposure.adjust_gamma(image, 0.67)
  image_3 = exposure.adjust_gamma(image, 25)
  # 分别展示原图和结果图像
  plt.subplot(2, 2, 1)
  plt.title('gamma=1')
  io.imshow(image)
  plt.subplot(2, 2, 2)
  plt.title('gamma=0.2')
  io.imshow(image_1)
  plt.subplot(2, 2, 3)
  plt.title('gamma=0.67')
  io.imshow(image_2)
  plt.subplot(2, 2, 4)
  plt.title('gamma=25')
  io.imshow(image_3)
  plt.show()
  
  

  当gamma=1，0.2,0.67,25时，运行结果如下：
  

  图17 图像点运算图

  六、实验结果分析
  （一）图像采样：采样是图像空间坐标的离散化，决定了图像的空间分辨率，是对原始图像信号的一种数字化逼近。从实验结果可以得出：当采样比率越低时，图像的空间分辨率越高，越接近原图像。

  （二）图像量化：采样后所得的各像素的灰度值从连续量到离散量的转换称为图像灰度的量化。从实验结果可以得出：图像的量化比率决定了图像的颜色精细程度。量化时确定的离散取值个数称为量化级，减少量化级数值能增强图像的反差。量化级越高，图像质量越好。

  （三）图像算术运算：图像运算是以图像为单位，对图像进行的数学操作，是数字图像信号处理的基础，运算对象以像素点为基本单位，运算结果为一幅灰度分布与原图像不同的新图像。
  （1）加法运算：用来生成叠加图像，可以得到各种合成图象
  （2）减法运算：去除不需要的叠加图像，检测同一场景两幅图像之间的变化。

  （四）图像点运算：点运算只涉及一幅图像（称为输入图像），运算对象是输入图像像素的灰度值，即输出图像每个像素的灰度值仅取决于输入图像中对应像素的灰度值。点运算可以分为线性点运算和非线性点运算。
  skimage的exposure模块中包含幂次变换的函数adjust_gamma（gamma调整）,可以对图像进行幂次变换。幂次变换为非线性变换。
  在生活中，很多图像由于光线原因或者曝光率等问题，导致图像过亮或过暗：因此，可以针对像素I进行幂指处理：

  其中，g是gamma参数。针对上式，从实验运行结果可以得出：
  （1）g>1，得到的图像比原始图像暗；
  （2）g<1，得到的图像比原始图像亮。
  八、实验总结
  （一）在采样时，若横向的像素数（列数）为M ，纵向的像素数（行数）为N，则图像总像素数为MN个像素。采样比率越高（间隔越大），所得图像像素数越少，空间分辨率低，质量差，当采样比率为20时，出现了马赛克效应；采样比率越低（间隔越小），所得图像像素数越多，空间分辨率高，图像质量好，但数据量大。
  （二）图像量化是将图像采样后的样本值的范围分为有限多个区域，落入某区域中的值用同一值表示，从而用有限的离散数值量来代替无限的连续模拟量。量化时确定的离散取值个数称为量化级数。
  若M、N为图像尺寸，K为每个像素所具有的离散灰度级数（不同灰度值的个数）。存一幅图像所需的位数（bit）B=MN*K ，当减少K值能增强图像的反差。当K值增加时，越能真实反映原有图像的颜色，但存储的字节也越大。
  因此，量化等级越多，所得图像层次越丰富，灰度分辨率高，图像质量好，但数据量大；量化等级越少，图像层次欠丰富，灰度分辨率低，会出现假轮廓现象，图像质量变差，但数据量小。
  （三）图像的加减法运算时要使用相同大小的图像，就是两个输入图像同一位置上的像素相加减，得到一个输出图像的过程。加法运算：用来生成叠加图像，可以得到各种合成图象，减法运算：去除不需要的叠加图像，检测同一场景两幅图像之间的变化。
  （四）点运算是根据某种预先设置的规则，将输入图像各个像素本身的灰度逐一转换成输出图像对应像素的灰度值。不会改变像素的空间位置。幂次变换属于点运算中的非线性变换。通过函数adjust_gamma（gamma调整）,可以对图像进行幂次变换。凸显图像中某些部分。其公式为:
  （1）g>1，得到的图像比原始图像暗；
  （2）g<1，得到的图像比原始图像亮。