学习笔记(1)LeNet-5
学习笔记(1)LeNet-5
参考博文
网络解析(一):LeNet-5详解
LeNet论文的翻译与CNN三大核心思想的解读
卷积神经网络的网络结构——以LeNet-5为例
LeNet5的深入解析
目录
一、前言
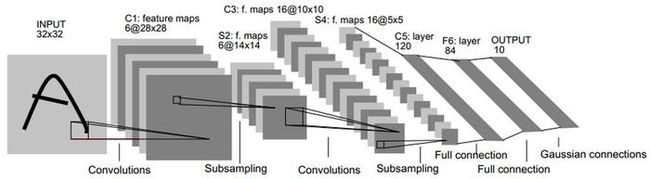
二、LeNet-5
三、代码实现
一、前言
LeNet-5[LeCun et al.,1998]虽然提出的时间比较早,但它是一个非常成功的神经网络模型。论文Gradient-Based Learning Applied to Document Recognition。基于LeNet-5的手写数字识别系统在20世纪90年代被美国很多银行使用,用来识别支票上面的手写数字。
二、LeNet-5
- LeNet-5 这个网络虽然很小,但是它包含了深度学习的基本模块:卷积层,池化层,全链接层。是其他深度学习模型的基础。
- LeNet-5共有7层,不包含输入,每层都包含可训练参数;每个层有多个Feature Map,每个FeatureMap通过一种卷积滤波器提取输入的一种特征,然后每个FeatureMap有多个神经元。
参数结构详解
- 如上图所示,可以对照图进行理解。
- 接受输入图像大小为32×32=1024,输出对应10个类别的得分。LeNet-5中每一层结构如下:
(1)C1层-卷积层
输入图片:32× 32
卷积核大小:5× 5
卷积核种类:6
输出featuremap大小:28× 28 (32-5+1)=28
神经元数量:28×28× 6
可训练参数:(5 × 5+1) × 6(每个滤波器5× 5=25个unit参数和一个bias参数,一共6个滤波器)
连接数:(5× 5+1)× 6×28× 28=122304
详细说明:使用6个5× 5 的卷积核,得到6组大小为28×28=784的特征映射(featureMap特征图)。因此C1层的神经元数量为6 × 28× 28=4704,可训练参数数量为 6×(5× 5+1)=156,连接数为156× 28×28=122304.
(2)S2层-池化层(下采样层)
输入:28× 28
采样区域:2× 2
采样方式:4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid
采样种类:6
输出featureMap大小:14× 14(28/2)
神经元数量:14× 14× 6
连接数:(2× 2+1)× 6× 14× 14
S2中每个特征图的大小是C1中特征图大小的1/4。
详细说明:第一次卷积之后紧接着就是池化运算,使用 2× 2核 进行池化,于是得到了S2,神经元个数为6× 14× 14=1176(28/2=14)。可训练参数为6× (1+1)=12,连接数为6× 14× 14× (4+1)=5880。
(3)C3层-卷积层
LeNet-5中用一个连接表来定义输入与输出的特征映射之间的依赖关系,如下图中的表所示:

(表中第1列表示C3的第0个特征图,与S2中的第0,1,2个特征图连接)
- 共使用60个5× 5的卷积核,得到16组大小为10× 10的特征映射(featureMap特征图),神经元数量为16× 10× 10=1600,可训练参数数量为(60× 5× 5)+16=1516,连接数为1516× 100=151600
连接规则:
- C3的前6个特征图与S2的相连3个特征图相连,对应的参数是6× (3× 5× 5+1)
- 接下来的6个特征图与S2的相连4个特征图相连,对应的参数是6× (4× 5× 5+1)
- 再接下来的3个特征图与S2的不相连4个特征图相连,对应的参数是3× (4× 5× 5+1)
- 最后一个特征图与S2所有的6个特征图相连,对应的参数是1*(6* 5* 5+1)
则:可训练参数:6× (3× 5× 5+1)+6× (4× 5× 5+1)+3× (4× 5× 5+1)+1× (6× 5× 5+1)=1516
连接数:10× 10× 1516=151600
也可以理解为16组不同的卷积核,(多通道卷积)每组卷积核包含D个5×5(用F×F表示)大小的卷积核。比如C3的第0个特征图,是由S2的前3层特征图(即D=3)与第0组(D=3)个5×5的卷积核卷积,再求和得到一个特征图,前6个map是这么卷积的。第6个特征图,是由S2前4层(即D=4)与第6组(D=4)5× 5的卷积核卷积再求和的。后面依次类推。
如果不使用连接表,则需要96个5*5的卷积核。(或理解为16组卷积核,每组D=6)
为什么不把S2中的所有特征图直接连接到每个C3的特征图呢?有两个原因。
- 不完全的连接机制可以使得连接数量保持在合理的范围内;(减少了参数)
- 破坏了网络对称性。不完全的连接可以保证C3中的特征图提取到不同的特征。
(4)S4层-池化层(下采样层)
输入:10× 10
采样区域:2× 2
采样方式:4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid
采样种类:16
输出featureMap大小:5× 5(10/2)
神经元数量:5× 5× 16=400
连接数:16× (2× 2+1)× 5× 5=2000
S4中每个特征图的大小是C3中特征图大小的1/4
详细说明:S4是pooling层,窗口大小仍然是2× 2,共计16个feature map,C3层的16个10x10的图分别进行以2x2为单位的池化得到16个5x5的特征图。可训练参数为16× 2=32,有16 * (2* 2+1)× 5× 5=2000个连接。连接的方式与S2层类似。
(5)C5层-卷积层
输入:S4层的全部16个单元特征map(与s4全相连)
卷积核大小:5× 5
输出featureMap大小:1× 1(5-5+1)
可训练参数/连接:120× (16× 5× 5+1)=48120
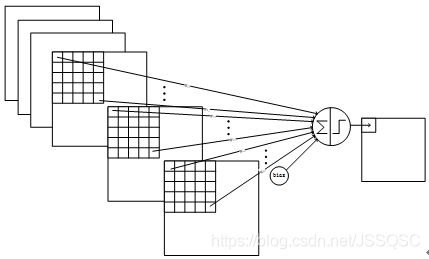
详细说明:C5层是一个卷积层。使用120× 16=1920个5× 5的卷积核(120组,每组通道数即D=16),得到120组1× 1大小的特征图。由于S4层的16个图的大小为5x5,与卷积核的大小相同,所以卷积后形成的图的大小为1x1。这里形成120个卷积结果。每个都与上一层的16个图相连。所以共有(5x5x16+1)x120 = 48120个可训练参数,同样有48120个连接。C5层的网络结构如下:
(6)F6层-全连接层
输入:c5 120维向量
计算方式:计算输入向量和权重向量之间的点积,再加上一个偏置,结果通过sigmoid函数输出。
可训练参数:84× (120+1)=10164
详细说明:6层是全连接层。F6层有84个神经元,对应于一个7x12的比特图,-1表示白色,1表示黑色,这样每个符号的比特图的黑白色就对应于一个编码。这种表示对识别单独的数字不是很有用,但是对识别可打印ASCII集中的字符串很有用。
该层的训练参数和连接数是(120 + 1)x84=10164。ASCII编码图如下:

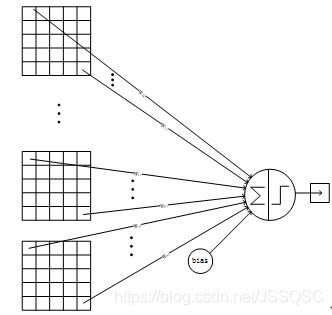
F6层的连接方式如下:
(7)Output层-全连接层
Output层也是全连接层,共有10个节点,分别代表数字0到9,且如果节点i的值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式。假设x是上一层的输入,y是RBF的输出,则RBF输出的计算方式是: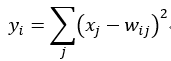
上式w_ij 的值由i的比特图编码确定,i从0到9,j取值从0到7× 12-1。RBF输出的值越接近于0,则越接近于i,即越接近于i的ASCII编码图,表示当前网络输入的识别结果是字符i。该层有84x10=840个参数和连接。
三、代码实现
基于Pytorch实现手写数字识别
# -*-coding:utf-8-*-
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
num_epochs = 5
num_classes = 10
batch_size = 100
learning_rate = 0.001
# MNIST dataset
train_dataset = torchvision.datasets.MNIST(root='data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = torchvision.datasets.MNIST(root='data/',
train=False,
transform=transforms.ToTensor())
# Data loader
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
class Lenet5(nn.Module):
def __init__(self, num_classes=10):
super(Lenet5, self).__init__()
self.c1 = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(6),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.c2 = nn.Sequential(
nn.Conv2d(6, 16, kernel_size=5),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.c3 = nn.Sequential(
nn.Conv2d(16, 120, kernel_size=5),
nn.BatchNorm2d(120),
nn.ReLU()
)
self.fc1 = nn.Sequential(
nn.Linear(120, 84),
nn.ReLU()
)
self.fc2 = nn.Sequential(
nn.Linear(84, num_classes),
nn.LogSoftmax()
)
def forward(self, x):
out = self.c1(x)
out = self.c2(out)
out = self.c3(out)
out = out.reshape(out.size(0), -1)
out = self.fc1(out)
out = self.fc2(out)
return out
model = Lenet5(num_classes).to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
# Forward pass
outputs = model(images)
loss = criterion(outputs, labels)
# Backward and optimize
optimizer.zero_grad()
loss.backward()
optimizer.step() # 优化 更参
if (i + 1) % 100 == 0:
print('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch + 1, num_epochs, i + 1, total_step, loss.item()))
# Test the model
model.eval() # eval mode (batchnorm uses moving mean/variance instead of mini-batch mean/variance)
with torch.no_grad():
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Test Accuracy of the model on the 10000 test images: {} %'.format(100 * correct / total))
torch.save(model.state_dict(), 'Lenet-5.ckpt')