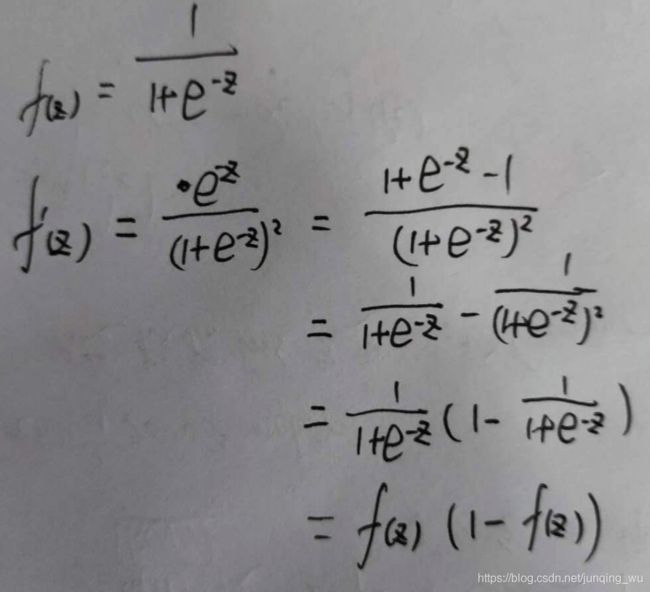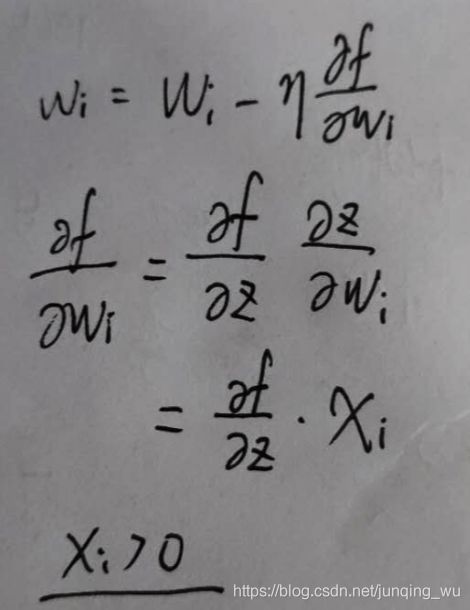常见激活函数 权重初始化

写在前面：
神经网络为什么需要激活函数：
如果不使用激活函数的话，网络整体(conv、pool、fc)是线性函数，线性函数无论叠加多少层，都是线性的，只是斜率和截距不同，叠加网络对解决实际问题没有多大帮助；而神经网络解决的问题大部分是非线性的，引入激活函数，是在神经网络中引入非线性，强化网络的学习能力。所以激活函数的最大特点就是非线性。

梯度消失、爆炸

• 反向传播算法计算误差项时每一层都要乘以本层激活函数的导数。如果激活函数导数的绝对值值小于1，多次连乘之后误差项很快会衰减到接近于0，参数的梯度值由误差项计算得到，从而导致前面层的权重梯度接近于0，参数没有得到有效更新，这称为梯度消失问题。
• 与之相反的是梯度爆炸问题，如果激活函数导数的绝对大于1，多次乘积之后权重值会趋向于非常大的数，这称为梯度爆炸。梯度消失问题最早在1991年发现，在很长一段时间内，梯度消失问题是困扰神经网络层次加深的一个重要因素

Sigmoid

问题

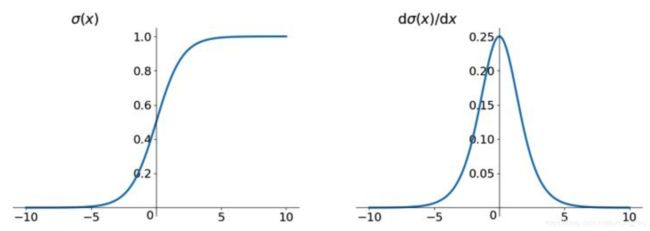
1. Sigmoid 极容易导致梯度消失问题，由于存在饱和现象，当数值在函数饱和区间时，梯度接近为0，经过多层网络反传，会发生梯度消失现象；
2. 计算费时，求导涉及复杂函数计算；
3. 不是中心对称

这个特性会导致后面网络层的输入也不是零中心的，进而影响梯度下降的运作。

因为如果输入都是正数的话（如 $f=w^{T}x+b$ 中每个元素都 $x>0$ ，那么关于 $w$ 的梯度在反向传播过程中，要么全是正数，要么全是负数（具体依据整个表达式 $f$ 而定 损失函数），这将会导致梯度下降权重更新时出现 z 字型的下降。

参考自

Tanh

问题

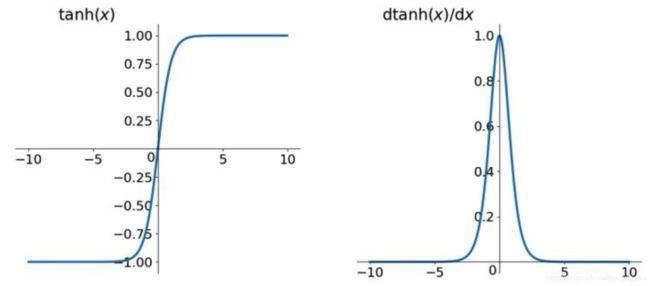
1. 输出为(-1,1)，解决了非零对称的问题，但是还是存在计算费时问题
2. tanh导数范围在(0, 1)之间，相比sigmoid的(0, 0.25)，梯度消失问题会得到缓解，但仍然还会存在，因为存在饱和现象；

Relu

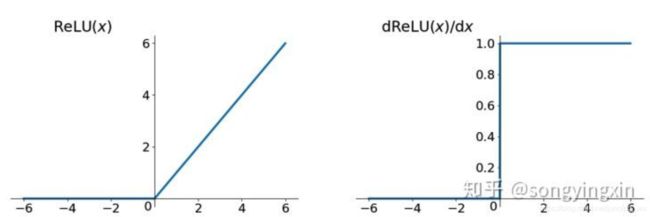
分段非线性函数，对ReLU求导，在输入值分别为正和为负的情况下，导数是不同的，即ReLU的导数不是常数，所以ReLU是非线性的（只是不同于Sigmoid和tanh，relu的非线性不是光滑的）。

特点

• 在x>0时，其导数恒为1,缓解了梯度消失问题(梯度消失还有其它复杂因素影响)，加速网络收敛，但是要小心梯度爆炸问题，因为神经元输出为max(0,n)，当激活值很大时，很容易造成梯度爆炸，所以一个解决方法是使用Relu6，限制其最大激活值
• 在x<0，会导致神经元死亡，即神经元的梯度为0，梯度不在更新，该神经元不会再次被激活，如果学习率设置过大，可能会造成大批量神经元死亡，导致网络不能学习到有效的特征表达；
• 但是神经元死活一定程度上也会带来稀疏的特性，可能有益于网络的鲁棒性；

优点

1. 相比Sigmoid和tanh，ReLU摒弃了复杂的计算，提高了运算速度。
2. 解决了梯度消失问题，收敛速度快于Sigmoid和tanh函数，但要防范ReLU的梯度爆炸
3. 容易得到更好的模型(权重稀疏性)，但也要防止训练中出现模型‘Dead’情况。

初始化

pytorch 默认初始化 reset_parameters(), 例如：nn.Linear 和 nn.Conv2D，都是在 [-limit, limit]之间的均匀分布，其中 limit 是 1. / sqrt(fan_in),fan_in是指参数张量的输入单元的数量

我们构建好网络，开始训练前，不能默认的将所有权重系数都初始化为零，因为所有卷积核的系数都相等时，提取特征就会一样，反向传播时的梯度也会存在对称性，网络会退化会线性模型。另外网络层数较深时，初始化权重过大，会出现梯度爆炸，而过小又会出现梯度消失。一般权重初始化时需要考虑两个问题：

1. 标准初始化

• 标准均匀初始化
  stand_uniform
  $W_{i,j}\sim gain\ast (-\sqrt{\frac{1}{fa{n}_{i}n}},\sqrt{\frac{1}{fa{n}_{i}n}})$

• 标准正态初始化
  stand_normal
  $W_{i,j}\sim gain\ast N(0,\sqrt{\frac{1}{fa{n}_{i}n}})$

2. Xavier初始化

• 均匀初始化
  xavier_uniform
  $W_{i,j}\sim gain\ast (-\sqrt{\frac{6}{fa{n}_{i}n+fa{n}_{o}ut}},\sqrt{\frac{6}{fa{n}_{i}n+fa{n}_{o}ut}})$

• 正态初始化
  xavier_normal
  $W_{i,j}\sim gain\ast N(0,\sqrt{\frac{2}{fa{n}_{i}n+fa{n}_{o}ut}})$

• gain 增益 理解为缩放系数

• fan_in 为 in_channel*k_w*k_h

• fan_out 为 out_channel*k_w*k_h

w = torch.empty(3, 3, 5, 5)          #fan_in=75, fan_out=75
nn.init.xavier_uniform_(w, gain=1)   #初始化为（-sqrt(6/150), sqrt(6/150)）范围内的均匀分布
nn.init.xavier_normal_(w, gain=1)    #初始化为mean=0, std=sqrt(2/150)的正态分布

计算fan_in fan_out 的代码

def _calculate_fan_in_and_fan_out(tensor):
    dimensions = tensor.dim()
    if dimensions < 2:
        raise ValueError("Fan in and fan out can not be computed for tensor with fewer than 2 dimensions")

    if dimensions == 2:  # Linear
        fan_in = tensor.size(1)
        fan_out = tensor.size(0)
    else:
        num_input_fmaps = tensor.size(1)
        num_output_fmaps = tensor.size(0)
        receptive_field_size = 1
        if tensor.dim() > 2:
            receptive_field_size = tensor[0][0].numel()
        fan_in = num_input_fmaps * receptive_field_size
        fan_out = num_output_fmaps * receptive_field_size

    return fan_in, fan_out

3.He初始化（ReLu建议使用）

• 均匀初始化
  xavier_uniform
  $W_{i,j}\sim gain\ast (-\sqrt{\frac{6}{fa{n}_{i}n}},\sqrt{\frac{6}{fa{n}_{i}n}})$

• 正态初始化
  xavier_normal
  $W_{i,j}\sim gain\ast N(0,\sqrt{\frac{2}{fa{n}_{i}n}})$

参数：
    tensor – n 维 torch.Tensor
    a – 该层后面一层的整流函数中负的斜率 (默认为 0，此时为 Relu)
    mode – ‘fan_in’ (default) 或者 ‘fan_out’。使用fan_in保持weights的方差在前向传播中不变；使用fan_out保持weights的方差在反向传播中不变。
    nonlinearity – 非线性函数 (nn.functional 中的名字)，推荐只使用 ‘relu’ 或 ‘leaky_relu’ (default)。

w = torch.empty(3, 3, 5, 5)          #fan_in=75, fan_out=75
nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu')   #初始化为（-sqrt(6/75), sqrt(6/75)）范围内的均匀分布
nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu')    #初始化为mean=0, std=sqrt(2/75)的正态分布

4. 均匀分布初始化