数据结构与算法-图---介绍了广度优先搜索、深度优先搜索、路径查找等算法的实现
概述:
本文主要讲解关于图的一系列知识,包括图的一系列专业术语、深度优先搜索、广度优先搜索、以及路径相关算法的介绍等。
专业术语介绍:
图的定义:图是由一组顶点和一组能够将两个顶点相连的边组成的。
度数:某个顶点的度数即为依附于它的边的总数
子图:子图是一幅图的所有边的一个子集(以及它们所依附的所有顶点)组成的图
路径:路径是由边顺序连接的一系列顶点
简单路径:简单路径是一条没有重复顶点的路径
环:环是一条至少含有一条边且起点和终点相同的路径
简单环:简单环是一条(除了起点和终点必须相同之外)不含有重复顶点和边的环
长度:路径或者环的长度为其中所包含的边数
连通:当两个顶点之间存在一条连接双方的路径时,我们称这两个顶点之间是连通的。
连通图:如果从任意一个顶点都存在一条路径到达另一个任意顶点,我们称这幅图是连通图
树:树是一幅无环连通图。互不相连的树组成的集合成为森林。连通图的生成树是它的一幅子图,它含有图中的所有顶点且是一棵树。
无向图:
无向图的数据类型:
图的表示方式:邻接矩阵、邻接表数组
因为后文应用的是邻接表数组,所以只简单介绍一下邻接表数组:所谓邻接表数组,就是我们使用一个以顶点为索引的列表数组,其中的每个元素都是和该顶点相邻的顶点列表,见下图。
基于邻接表的Graph数据结构实现(也就是上方表4.1.1的API的实现):
public class Graph{
private final int V; //顶点数目
private int E; //边的数目
private Bag<Integer>[] adj //邻接表,关于Bag类,可见《算法4》p76,就是一个无序容器
//构造函数
public Graph(int V){
this.V=V;
this.E=E;
adj=(Bag<Integer>[]) new Bag[V]; //创建邻接表
for(int v=0; v<V; v++){ //将所有链表初始化为空
adj[v]=new Bag<Integer>();
}
}
//返回顶点个数
public int V() { return V; }
//返回边数
public int E() { return E;}
//给两个顶点之间添加边(注意:因为是基于邻接表数组的实现,所以对于无向图来说,添加边时,需要同时在两个顶点后面的邻接表内分别添加对方)
public void addEdge(int v, int w){
adj[v].add(w); //将w添加到v的链表中
adj[w].add(v); //将v添加到w的链表中
E++;
}
//以Iterable类型的形式返回和v相邻的所有顶点
public Iterable<Integer> adj(int v){
return adj[v];
}
}
图的处理算法的设计模式
因为我们会讨论大量的关于图处理的算法,所以设计的首要目标是将图的表示和实现分离开来。为此,我们会为每个任务创建一个相应的类,用例可以创建相应的对象来完成任务。类的构造函数一般会在预处理中构造各种数据结构,以有效的响应用例的请求。典型的用例程序会构造一幅图,将图传递给实现了某个算法的类(作为构造函数的参数),然后调用用例的方法来获取图的各种性质。所以,图的处理算法的模板API如下:
有了这个图的处理算法的模板API,接下来我们将会介绍图的两个非常重要的处理算法。
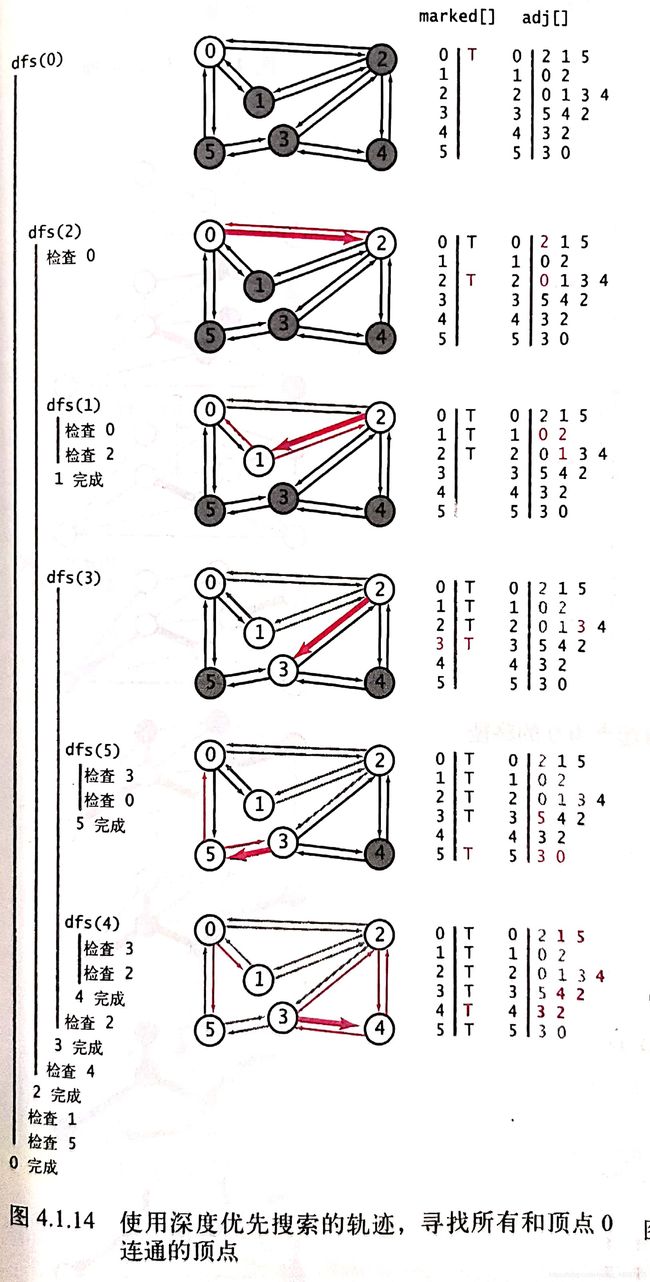
深度优先搜索:
深度优先搜索算法API的实现:
public class DepthFirstSearch{
private boolean[] marked;
private int count;
public DepthFirstSearch(Grapg G, int s){
marked= new boolean[G.V()];
dfs(G,s);
}
//深度优先搜索算法的实现
private void dfs(Graph G, int v){
marked[v]=true;
count++;
for(int w : G.adj(v))
if(!marked[w]) dfs(G,w);
}
public boolean marked(int w){ //查看顶点w的状态,看是否已经被访问过
return marked[w];
}
public int count(){
return count;
}
}
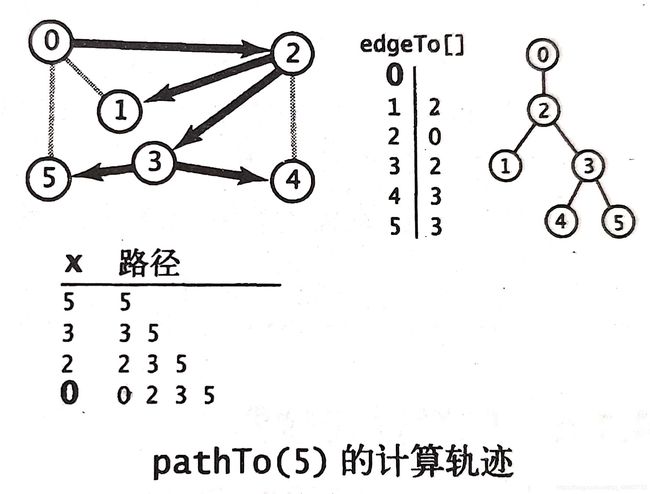
路径寻找算法:
算法API模板:
使用深度优先搜索实现图中的路径查找算法:
public class DepthFirstPaths{
private boolean[] marked; //用以标记某个顶点上是否使用过dfs()
private int[] edgeTo; //从起点到一个顶点的已知路径上的最后一个顶点
private final int s; //起点
public DepthFirstPaths(Graph G, int s){
marked=new boolean[G.V()];
edgeTo=new int[G.V()];
this.s=s;
dfs(G,s);
}
private void dfs(Graph G, int v){
marked[v]=true;
for(int w : G.adj(v))
if(!marked[w]){
edgeTo[w]=v;
dfs(G,w);
}
}
public boolean hasPathTo(int v){
return marked[v];
}
public Iterable<Integer> pathTo(int v){
if(!hasPathTo(v)) return null;
Stack<Integer> path=new Stack<Integer>();
for(int x=v; x!=s; x=edgeTo[x])
path.push(x);
path.push(s);
return path;
}
}
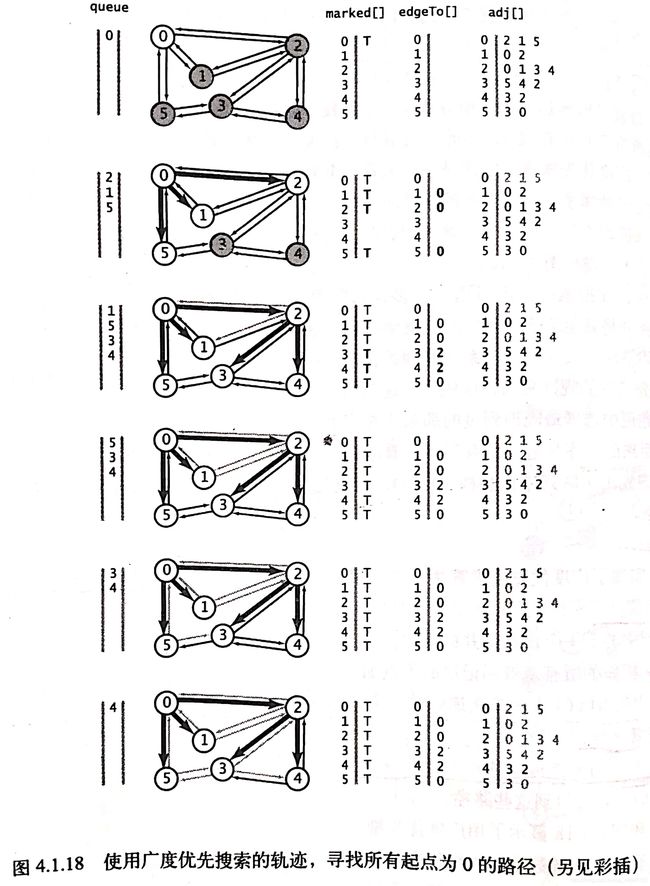
广度优先搜索
用处:用于解决最短路径的问题
算法实现:
public class BreadthFirstPaths{
private boolean[] marked; //到达该顶点的最短路径已知吗?
private int[] edgeTo; //到达该顶点的已知路径上的最后一个顶点
private final int s; //起点
public BreadthFirstPaths(Graph G, int s){
marked=new boolean[G.V()];
edgeTo=new int[G.V()];
this.s=s;
bfs(G,s);
}
//广度优先搜索算法实现
private void bfs(Graph G, int s){
Queue<Integer> queue=new Queue<Integer>();
marked[s]=true; //标记起点
queue.enqueue(s); //将它加入队列
while(!queue.isEmpty()){
int v=queue.dequeue(); //从队列中删去下一个顶点
for(int w : G.adj(v))
if(!marked[w]){ //对于每个未被标记的相邻顶点
edgeTo[w]=v; //保存最短路径的最后一条边
marked[w]=true; //标记它,因为最短路径已知
queue.enqueue(w); //并将它添加到队列中
}
}
}
public boolean hasPathTo(int v){
return marked[v];
}
public Iterable<Integer> pathTo(int v){
//和深度优先搜索中的实现相同
}
}
参考书籍:
[1] 程杰. 大话数据结构. 北京:清华大学出版社,2011
[2] Robert Sedgewick, Kevin Wayne. 算法(第四版). 人民邮电出版社