Global Illumination_AMD FSR 算法
一、AMD FSR简介
AMD FidelityFX Super Resolution,简称FSR,中文名称是“AMD超级分辨率锐画技术”。就是使用超分辨率技术实现高分辨率,高品质游戏画面,并显著提高游戏运行效率的一套实现方法和程序库。它免费开源(https://github.com/GPUOpen-Effects/FidelityFX-FSR),跨平台,针对硬件进行了优化,集成到程序也非常简单(实际上只有两个文件),最神奇的是,运行它并不需要特殊的硬件,甚至如前几代的Intel CPU内集成的核显,都可以使用该技术。如果现在你在开发一个新的次时代画面游戏,真是没有理由不使用它。
如果要用一句话说明白FSR是如何工作的,总结了如下公式:
FSR = 放大(Upsacling) + 锐化(Sharpening)

是的,就是如此简单。在放大的步骤,FSR实际上通过算法实现了对图形边缘的检测,在放大图像的同时尽量保持原有的边缘,从而实现超分辨率。往往超分辨率算法会产生类似模糊或虚影的错误,FSR使用了一个锐化步骤来消除超分辨率的这个副作用。对AMD技术熟悉的朋友大概还记得AMD曾经推出过一个锐化技术:AMD FidelityFX Contrast Adaptive Sharpening, 简称CAS,没错,这里复用了该技术,并对其进行了针对性优化,使得最终的图像质量得以保证
而FSR在渲染流水线中的位置,大概位于实际渲染完成以后,部分后处理(Post-processing)之前,你可以把FSR看做是后处理的一部分,只不过要十分小心FSR在后处理栈中所处的位置,避免一些后处理导致FSR处理错误,影响最终的图像质量。

比如胶片噪点(Film grain)效果,在很多追求电影式画面的游戏中广泛使用,该效果产生的噪点就会影响FSR的发挥,(FSR会加强这些噪点的存在感)使得最终画面出现错误。
二、超分辨率的算法
超分辨率算法大致可以看做是一种插值算法,简单来说就是“无中生有”的算法。提高图像的分辨率意味着要向其中添加像素,那么新添加的像素是什么颜色呢?最简单最自然的想法,就是在已知的像素中间插值。
当前的超分辨率算法可以大致分为两种:基于数值插值的方法,和基于AI的方法。许多算法可能要求使用多帧的数据,为简单起见,我们在这里仅讨论使用单帧图像的情况。
2.1 最近点采样(Nearest neighbor sample)和双线性插值(Bilinear interpolation)
这两种方法通常用在普通的贴图过滤采样中,被叫做最近点过滤和双线性过滤。所谓的过滤,是指模型渲染到屏幕上时可能被缩放,所以屏幕上的一个点可能对应贴图上的多个像素,也可能是屏幕上的多个点只能对应贴图上一个点。也就是说这两种方法不但可以处理图像放大,还可以在图像缩小的时候发挥作用。
现如今很少使用这两种方法来做超分辨率了,但是这两种方法是硬件能够直接支持的方法,也是其他数值方法的基础,所以在这里做一下简单介绍。
最近点采样方法十分直接,插值出的像素,直接复用它距离它最近像素的颜色。缺点也很明显,图形边缘会出现锯齿状走样,俗称“狗牙”。
双线性插值更进一步,使用周围4个像素来计算一个“平均颜色”,可以有效减少锯齿,但缺点同样明显,会使得图形边缘变得模糊不清。
2.2 两次立方插值(Bicubic interpolation)
两次立方方法广泛应用在各种图像算法中,两次立方插值实际上是采样了更多周围像素的结果,通过对周围像素使用不同的权重,得到的“平均颜色”更加接近应有的结果。
在很多照片处理软件,数码相机以及手机摄像组件中,对数字图像的旋转缩放等处理都使用了该方法。该方法的缺点是要采样更多的像素,运算量比较大,通常不会用在需要实时处理的领域。
2.3 Lanczos插值(Lanczos interpolation)
Lanczos方法也是应用广泛的数值方法,在物理、机械、工程、图像各种领域都有应用。FSR正是使用了Lanczos的简化方法来进行插值,具体的应用方法详见下文。
Lanczos插值的结果与两次立方插值是接近的,但是由于其可以用较少的采样点达到近似的效果,因此在实时程序中应用更广泛一些。
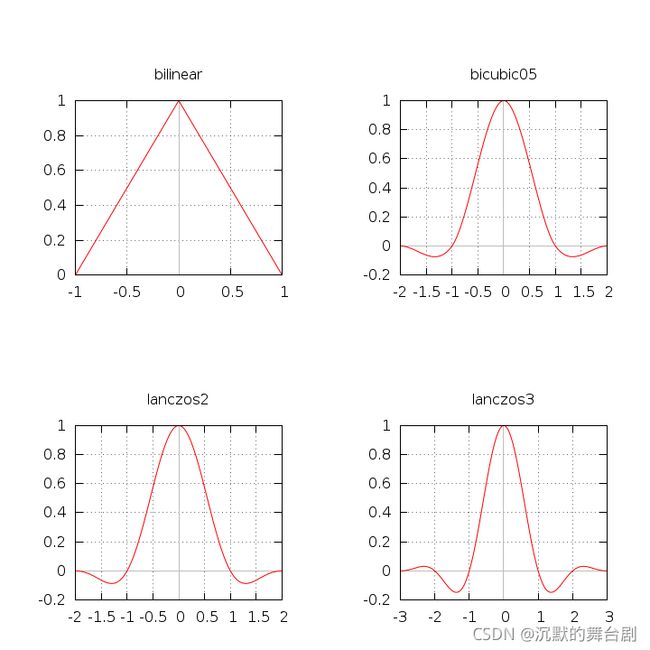
下图对比了各种算法在平面直角坐标系下的区别。
2.4 基于人工神经网络的方法
基于AI深度学习的超分辨率是如今的大热门话题,通过选择合适的神经网络模型和大量的训练,深度学习方法可以产生非常准确的图像,尤其是在分辨率放大倍数特别大的情况下要明显优于纯数值方法。除去超分辨率之外,基于AI深度学习的方法还可以提供包括降噪和锐化等额外的效果,而数值方法则需要更多处理步骤来实现。NVIDIA的DLSS就是属于这一类方法。
NVIDIA DLSS(深度学习超采样Deep Learning Super Sampling)是NVIDIA为其RTX系列显卡开发的一个程序库,可以将低分辨率的游戏画面转换为高分辨率,使用时下流行的AI计算方法去除错误增加质量,实际上也是跟FSR一样的功效:既可以超分辨率处理,也可以负担抗锯齿的任务,DLSS具体的模型算法目前并未公开。
神经网络计算虽然看起来高大上,但需要大规模的并行计算能力,在超分辨率实时应用中往往会挤占本来就非常紧张的计算资源。比如NVIDIA的DLSS就是利用图形渲染时可能会闲置的AI计算核心(Tensor Core)来计算超分辨率。而且NVIDIA只允许拥有TensorCore的RTX系列开启DLSS功能,因为直接使用通用计算单元的话可能就会适得其反,不但效率得不到提升,反而会拖慢整个渲染。这也是为什么10系的N卡无法使用DLSS。

神经网络计算的另一个弊端就是前期需要大量的数据进行训练。 比如DLSS原始版本和DLSS 2.0就需要使用NVIDIA NGX超级计算机预先进行训练,并且需要开发团队提供数千帧超大分辨率的游戏画面作为训练数据输入。DLSS 2.1及以后的版本神经网络已经稳定,所有游戏就统一使用同样的模型进行计算了。
除以上所列出的以外,还有很多其他算法,比如基于时序的数值算法(用于视频处理),棋盘格渲染(SONY PlayStation4曾经有使用过)等等,限于篇幅此处不作展开。
三、FSR的原理
上文提到一个公式,FSR= 放大+锐化,实际上FSR由两个分别负责放大和锐化的组件组成:
- 边缘自适应空间上采样EASU(Edge Adaptive Spatial Upsampling)
- 稳定对比度自适应锐化RCAS(Robust Contrast Adaptive Sharpening)
3.1 EASU的工作原理
EASU是超分辨率的核心。EASU通过优化的采样策略从原始图像上取得附近的像素,对其进行插值计算得到目标像素。
其算法有可以大致分为三个阶段:
-
一阶段:像素采样
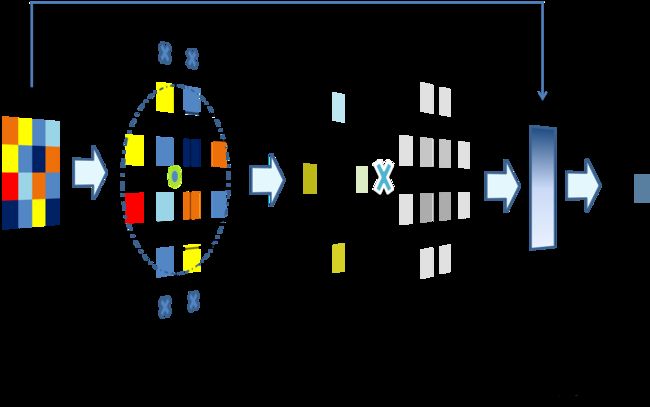
它使用一个圆形的采样区域来尽量减少采样的像素,通过特别计算的采样点,直接利用硬件支持的双线性采样函数进行采样,最大限度降低采样次数。 -
二阶段:插值计算
这部分是整个算法中最复杂的一部分,首先是积累计算线性插值的方向和长度,然后在所有方向上计算Lanczos插值。此处FSR对Laczos-2算法进行了数值近似,去掉了原有的三角函数和开方运算以提高效率。 -
三阶段:限制输出
由于Lanczos-2函数会产生值小于0的部分(见图 各种算法的核函数),在某些情况下回出现一个环形的失真,所以在得到最终结果后,将结果限制在临近4个像素的最大和最小值之间。
另外,对于支持16bit半精度计算的硬件,FSR将使用打包的16bit模式(Packed 16bit),可以使得2个16bit数据并行计算以提高性能;对于不支持的硬件,将回退到32bit模式,这将造成一定的性能损失。
3.2 RCAS的工作原理
AMD的FidelityFX CAS技术,是使用像素点附近的局部对比度(Local Contrast)对颜色进行调整,以消除因为抗锯齿,图像拉伸等操作造成的细节模糊。
RCAS在此基础上进行了进一步的优化,去掉了CAS对图像拉伸的支持(该功能已经由EASU实现了),并且直接使用最大局部锐度进行解算。

由于FSR对局部变化比较大(高频)的区域敏感,所以在FSR处理之前图像不可以有任何添加噪点的后处理操作,如果有必要还应添加抗锯齿(反走样)流程。此外FSA还提供了一些额外的功能,如下:
-
线性胶片颗粒 LFGA (Linear Film Grain Applicator) 用于在缩放图像后添加胶片颗粒的算法
-
简单可逆调和映射 SRTM (Simple Reversible Tone-Mapper)线性的动态高范围(HDR)可逆映射器
-
时序能量保存抖动 TEPD (Temporal Energy Preserving Dither) 一个将图像从线性空间转到Gamma 2.0空间的映射器
四、FSR的实现
4.1 EASU (Edge Adaptive Spatial Upsampling)
在这一步的处理中,将低分辨率的纹理通过自适应上采样的方式放大到目标分辨率。
4.1.1 上采样(upsampling),下采样(downsampling)
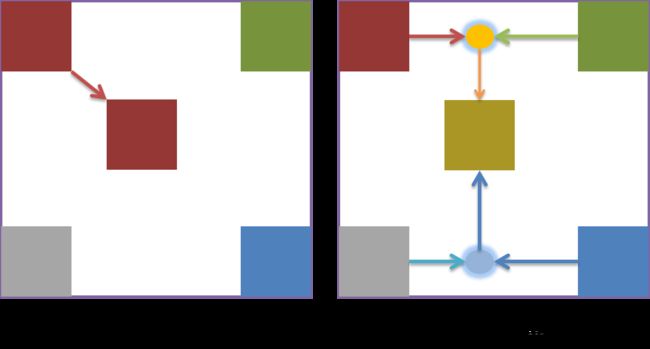
上采样和下采样都是对纹理进行重新采样(Resampling)的两种方式
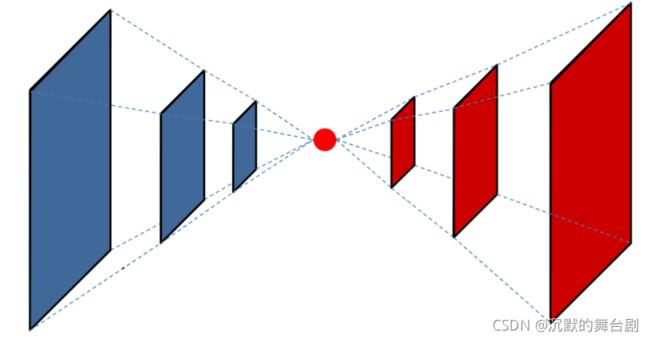
从蓝色到1个点是下采样,从一个点到红色是上采样
-
上采样:就是把原来的纹理放大,然后空的部分通过比如线性插值之类的进行填充。
-
下采样:就是把原来的纹理缩小,缩小的方式很多比如mipmap就是把四个像素取平均值算做一个。
4.1.2 边缘与非边缘的上采样
当采用EASU上采样将纹理放大之后,空出来的像素点需要填充,此时就有两种情况:
- 非边缘: 如果是非边缘的情况,对于采样的像素点 P 周围像素的灰度值应该与像素点 P 非常接近,那么像素点 P
只需要进行加权平均即可:

放大之后的纹理上的像素点 P 对应原始纹理的像素点为 Q , Qi 为像素点 Q 周围的像素点, f(x) 为采样点 x 的灰度值,wi 为权重(为正)。
任何颜色都有红、绿、蓝三原色组成,假如原来某点的颜色为RGB (R, G, B),那么,我们可以通过下面几种方法,将其转换为灰度:
1.浮点算法: Gray = R*0.3+G*0.59+B*0.11
2.整数方法: Gray = (R*30+G*59+B*11)/100
3.移位方法: Gray = (R*28+G*151+B*77)>>8
4.平均值法: Gray = (R+G+B) /3
5.仅取绿色: Gray = G;
通过上述任一种方法求得Gray后,将原来的RGB (R, G, B)中的R, G, B统一用Gray替换,形新的颜色RGB (Gray, Gray, Gray),用它替换原来的RGB (R, G, B)就是灰度图了。
- 边缘: 此时如果采样的像素点 P 应该为边缘,再按照式非边缘处理那势必会把边缘处理的很模糊。根据边缘锐化的思路,对边缘进行上采样为:

其中 F(Q) 为一个高频滤波器, λ 用来缩放 F(Q) 。
如果 Qx,y 周围的像素灰度值变化越小(低频)则 F(Q) 越小,灰度值变化越大(高频)则 F(Q) 越大。
所谓高频滤波,关键是求某一像素点与周围像素点的差值,本质上还是加权法,只不过这里的权重有为负(为负是为了计算差值)。
那既然对于边缘也可以用加权来做上采样,EASU因此提出了一种统一的表达式:

其中 H(Qi) 为权重计算公式,并且应该满足,当 Q 点不为边缘的时候应该为正;当 Q 点为边缘的时候应该包括为负的权重用于计算高频滤波器,因此最关键的就是针对是否为边缘确定负权重。
当然可以直接采用公式 f ( P ) =f(Q) + λF(Q) 的方式来上采样,但是如此就做不到针对每个像素做出不同的上采样策略,很容易导致图片噪点。
4.1.3 Lanczos2 函数
因此EASU引入了Lanczos函数:
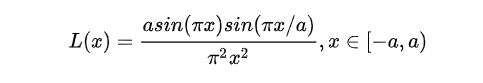
当 α 取2的时候通常将其称作Lanczos2 函数,EASU都是以Lanczos2 函数作为基础处理的。先来看看Lanczos2 函数图像:

Lanczos2的图像看起来平平无奇,不过大家注意 x∈[0,1] 部分函数值大于0, x∈[1,2] 部分,函数值小于0.
EASU提出可以通过多项式来拟合下公式
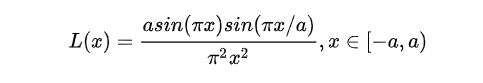
同时映入一个变量来控制 w 的函数值:
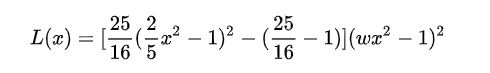
其中 w 是用于控制函数值的变量。再来看看函数图像:
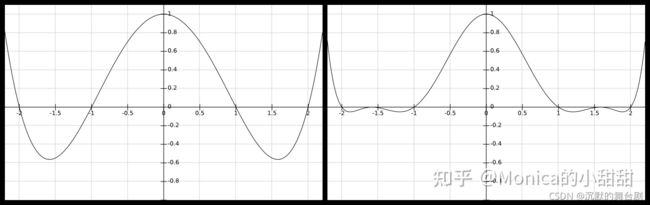
是不是感觉有点希望了! 区间 x∈[1,2] 的负半轴明显发生变化,那接下来还有个问题就是如何确定某个像素是否为边缘。
4.1.4 边缘特征
边缘大概分为上面三种,但EASU主要解决第1,2种边缘类型。因此特征越像第1,2种类型则 w 越小,同时对于像素点 Q 只计算上下左右方向的像素点,如图所示。
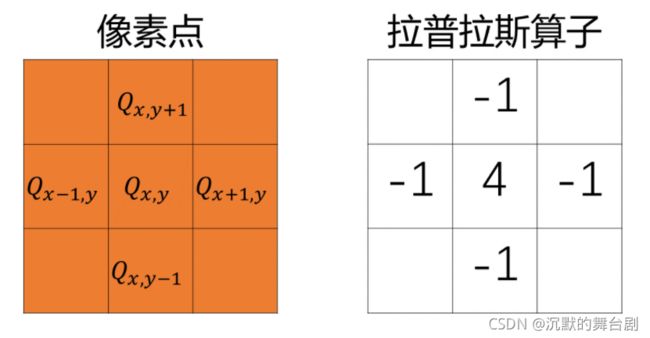
EASU定义的边缘特征 F 计算公式为:
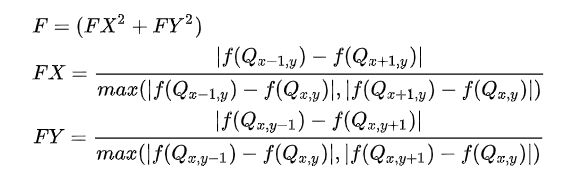
注意,上面的计算都需要先转为灰度值,并且 FX,FY∈[0,1] 。需要注意的是由于是直接加上XY方向因此 F∈[0,2] ,因此EASU提出将其映射到 [0,1] :

如此一来就针对第1,2种边缘类型计算出了边缘特征 Feature (根据本小节上述两公式,越趋近1、2种边缘类型, Feature 越大)。
那么接下来的问题就是如何建立边缘特征 Feature 与 w 的联系?
4.1.5 边缘特征 Feature 与 变量 w
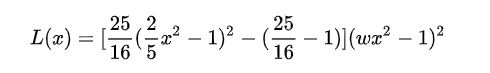
还是从拟合的公式函数 *** L(x),x∈[-2,2]*** 入手(由于 *** L(x)*** 关于 *** y*** 轴对称,下面的分析只针对正半轴):
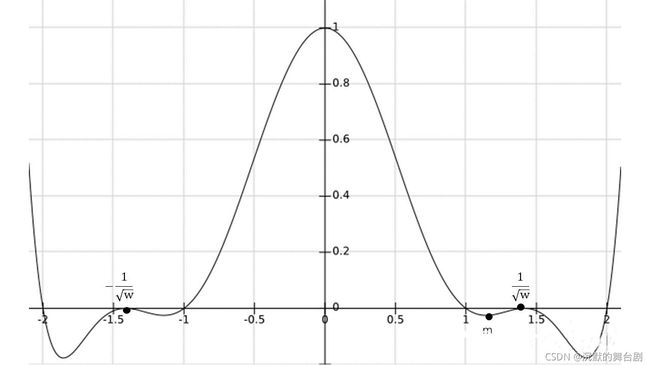
如上图所示,在正半轴 *** L(x)*** 的根:

情况一:
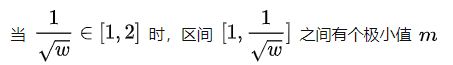
分析可知:
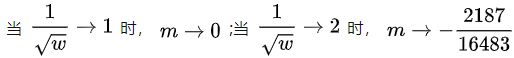
因此,只需要改变 1/√w 的大小(当然必须属于 [1,2] 区间),就可以很容易操控区间 [1,1/√w] 负值大小(用来作为上采样统一表达式的负权重);
所以
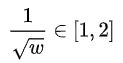
可以解得:

根据上述分析确定了 w 与区间 [1,1/√w] 中负值(负权重)的关系。因此可以很容易的建立一个 边缘特征 Feature 与 变量 w 的线性关系( Feature=1 时***w=1/4*** , Feature=0 时***w=1*** ):
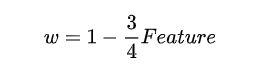
但在实际使用过程中由于 1/√w 趋于1时负权重不够,进而导致部分区域边缘信息识别不够。因此EASU 限定 1/√w 范围为 [√2,2] ,分析同上可以解出 *** w∈[1/4,1/2]*** ,同时可以得出一个新的边缘特征 Feature 与 变量 w 的线性关系:
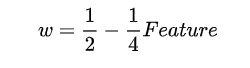
至此就建立了边缘信息与Lanczos2 函数的关系。:对于区间 [1,1/√w] ,对于区间 [1/√w,2] 直接裁剪,即:

4.1.6 双线性插值
如果对于像素 Q 单单只计算上下左右四个像素可能会导致毕竟大的偏差,因此为了更加准确EASU还提出了一种双线性插值。如上图所示,对于像素 Q 采样他周围12个像素,然后按照上面不同颜分成四组,根据公式计算出四组 w 然后采用双线性插值。接下来的问题就是如何计算双线性插值的权重。
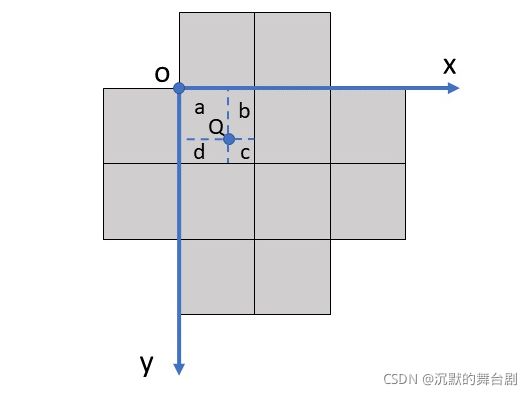
Q 点通常不是整数, O=floor(Q) 。假设 Q 点在以 O 点为原点的坐标系中坐标为 [公式] ,则双线性插值之后的结果为:
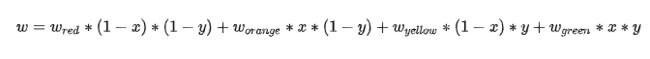
4.1.7 旋转和缩放
为了更加适宜各种角度的边缘,EASU还提出可以进行旋转。首先计算出 xy 的梯度:
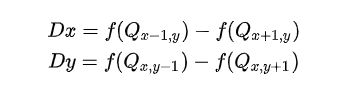
注意:梯度的计算仍然需要采用4.1.6提出的双线性插值计算。
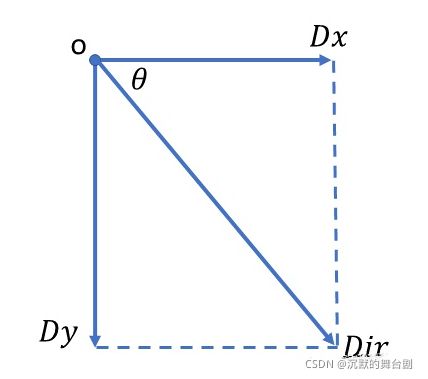
对于梯度向量 Dir=(Dx,Dy) 的意义就在于,沿着该向量方向是灰度值变换最快的方向,也就是说边缘垂直于梯度向量 Dir 。所以可以直接采用梯度旋转采样点 (x,y) ,首先将 Dir 进行归一化(需要注意***Dx=Dy=0*** 的情况),此时 Dir=(cosθ,sinθ) ,旋转之后的坐标为:
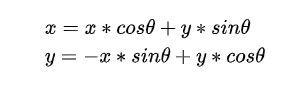
为了减少锯齿,EASU还提出可以根据梯度和边缘信息进行缩放,EASU定义的缩放比例为(注意,这里是直接定义的公式并没有数学逻辑):

至此,EASU结束,成功的对图像进行了自适应上采样!!!
4.1.8 计算着色器代码
#version 430 core
#pragma optionNV (unroll all)
#define LOCAL_GROUP_SIZE 32
layout(local_size_x = LOCAL_GROUP_SIZE, local_size_y = LOCAL_GROUP_SIZE) in;
layout(rgba32f, binding = 0) uniform writeonly image2D u_OutputEASUTexture;
uniform sampler2D u_InputTexture;
uniform int u_DisplayWidth;
uniform int u_DisplayHeight;
uniform vec4 u_Con0;
uniform vec4 u_Con1;
uniform vec4 u_Con2;
uniform vec4 u_Con3;
vec4 fsrEasuRF(vec2 p) { vec4 res = vec4(textureGather(u_InputTexture, p, 0)); return res; }
vec4 fsrEasuGF(vec2 p) { vec4 res = vec4(textureGather(u_InputTexture, p, 1)); return res; }
vec4 fsrEasuBF(vec2 p) { vec4 res = vec4(textureGather(u_InputTexture, p, 2)); return res; }
vec3 min3F3(vec3 x, vec3 y, vec3 z) { return min(x, min(y, z)); }
vec3 max3F3(vec3 x, vec3 y, vec3 z) { return max(x, max(y, z)); }
void fsrEasuTapF(
inout vec3 aC, // Accumulated color, with negative lobe.
inout float aW, // Accumulated weight.
vec2 Off, // Pixel offset from resolve position to tap.
vec2 Dir, // Gradient direction.
vec2 Len, // Length.
float w, // Negative lobe strength.
float Clp, // Clipping point.
vec3 Color) { // Tap color.
//公式15
vec2 v;
v.x = (Off.x * (Dir.x)) + (Off.y * Dir.y);
v.y = (Off.x * (-Dir.y)) + (Off.y * Dir.x);
//公式16
v *= Len;
float x2 = v.x * v.x + v.y * v.y;
//根据w裁剪
x2 = min(x2, Clp);
//公式6
// (25/16 * (2/5 * x^2 - 1)^2 - (25/16 - 1)) * (1/4 * x^2 - 1)^2
// |_______________________________________| |_______________|
// base window
float WindowB = float(2.0 / 5.0) * x2 + float(-1.0);
float WindowA = w * x2 + float(-1.0);
WindowB *= WindowB;
WindowA *= WindowA;
WindowB = float(25.0 / 16.0) * WindowB + float(-(25.0 / 16.0 - 1.0));
float Window = (WindowB * WindowA);
aC += Color * Window; aW += Window;
}
//根据公式7计算Feature,根据公式14计算梯度Dir
void fsrEasuSetF(
inout vec2 Dir,
inout float Feature,
vec2 P,
bool BoolS, bool BoolT, bool BoolU, bool BoolV,
float LumaA, float LumaB, float LumaC, float LumaD, float LumaE) {
// s t
// u v
float Weight = 0.0f;
if (BoolS) Weight = (1.0f - P.x) * (1.0f - P.y);
if (BoolT) Weight = P.x * (1.0f - P.y);
if (BoolU) Weight = (1.0f - P.x) * P.y;
if (BoolV) Weight = P.x * P.y;
float DC = LumaD - LumaC;
float CB = LumaC - LumaB;
float FeatureX = max(abs(DC), abs(CB));
float DirX = LumaD - LumaB;
Dir.x += DirX * Weight;
FeatureX = clamp(abs(DirX) / FeatureX, 0.0f, 1.0f);
FeatureX *= FeatureX;
Feature += FeatureX * Weight;
// Repeat for the y axis.
float EC = LumaE - LumaC;
float CA = LumaC - LumaA;
float FeatureY = max(abs(EC), abs(CA));
float DirY = LumaE - LumaA;
Dir.y += DirY * Weight;
FeatureY = clamp(abs(DirY) / FeatureY, 0.0f, 1.0f);
FeatureY *= FeatureY;
Feature += FeatureY * Weight;
}
vec3 fsrEasuF(ivec2 ip)
{
// +---+---+
// | | |
// +--(0)--+
// | b | c |
// +---F---+---+---+
// | e | f | g | h |
// +--(1)--+--(2)--+
// | i | j | k | l |
// +---+---+---+---+
// | n | o |
// +--(3)--+
// | | |
// +---+---+
//------------------------------------------------------------------------------------------------------------------------------
vec2 P = vec2(ip) * u_Con0.xy + u_Con0.zw;
vec2 F = floor(P);
P -= F;
vec2 P0 = F * u_Con1.xy + u_Con1.zw;
vec2 P1 = P0 + u_Con2.xy;
vec2 P2 = P0 + u_Con2.zw;
vec2 P3 = P0 + u_Con3.xy;
vec4 bczzR = fsrEasuRF(P0);
vec4 bczzG = fsrEasuGF(P0);
vec4 bczzB = fsrEasuBF(P0);
vec4 ijfeR = fsrEasuRF(P1);
vec4 ijfeG = fsrEasuGF(P1);
vec4 ijfeB = fsrEasuBF(P1);
vec4 klhgR = fsrEasuRF(P2);
vec4 klhgG = fsrEasuGF(P2);
vec4 klhgB = fsrEasuBF(P2);
vec4 zzonR = fsrEasuRF(P3);
vec4 zzonG = fsrEasuGF(P3);
vec4 zzonB = fsrEasuBF(P3);
//------------------------------------------------------------------------------------------------------------------------------
vec4 bczzL = bczzB * 0.5f + (bczzR * 0.5f + bczzG);
vec4 ijfeL = ijfeB * 0.5f + (ijfeR * 0.5f + ijfeG);
vec4 klhgL = klhgB * 0.5f + (klhgR * 0.5f + klhgG);
vec4 zzonL = zzonB * 0.5f + (zzonR * 0.5f + zzonG);
// Rename.
float bL = bczzL.x;
float cL = bczzL.y;
float iL = ijfeL.x;
float jL = ijfeL.y;
float fL = ijfeL.z;
float eL = ijfeL.w;
float kL = klhgL.x;
float lL = klhgL.y;
float hL = klhgL.z;
float gL = klhgL.w;
float oL = zzonL.z;
float nL = zzonL.w;
vec2 Dir = vec2(0.0);
float Feature = 0.0;
// 双线性插值
fsrEasuSetF(Dir, Feature, P, true, false, false, false, bL, eL, fL, gL, jL);
fsrEasuSetF(Dir, Feature, P, false, true, false, false, cL, fL, gL, hL, kL);
fsrEasuSetF(Dir, Feature, P, false, false, true, false, fL, iL, jL, kL, nL);
fsrEasuSetF(Dir, Feature, P, false, false, false, true, gL, jL, kL, lL, oL);
//------------------------------------------------------------------------------------------------------------------------------
//
{//归一化梯度向量Dir
vec2 Dir2 = Dir * Dir;
float DirR = Dir2.x + Dir2.y;
bool Zero = DirR < (1.0 / 32768.0);
DirR = 1.0f / sqrt(DirR);
DirR = Zero ? 1.0f : DirR;
Dir.x = Zero ? 1.0f : Dir.x;
Dir *= vec2(DirR);
}
{//公式8
Feature = Feature * 0.5f;
Feature *= Feature;
}
//公式16
float Stretch = (1.0f / (max(abs(Dir.x), abs(Dir.y))));
vec2 Len = vec2(1.0f + (Stretch - 1.0f) * Feature, 1.0f + -0.5f * Feature);
//公式11
float w = 0.5f - 0.25f * Feature;
//公式12
float Clp = 1.0f / w;
vec3 Min4 = min(min3F3(vec3(ijfeR.z, ijfeG.z, ijfeB.z), vec3(klhgR.w, klhgG.w, klhgB.w), vec3(ijfeR.y, ijfeG.y, ijfeB.y)),
vec3(klhgR.x, klhgG.x, klhgB.x));
vec3 Max4 = max(max3F3(vec3(ijfeR.z, ijfeG.z, ijfeB.z), vec3(klhgR.w, klhgG.w, klhgB.w), vec3(ijfeR.y, ijfeG.y, ijfeB.y)),
vec3(klhgR.x, klhgG.x, klhgB.x));
// Accumulation.
vec3 aC = vec3(0.0);
float aW = (0.0);
fsrEasuTapF(aC, aW, vec2(0.0, -1.0) - P, Dir, Len, w, Clp, vec3(bczzR.x, bczzG.x, bczzB.x)); // b
fsrEasuTapF(aC, aW, vec2(1.0, -1.0) - P, Dir, Len, w, Clp, vec3(bczzR.y, bczzG.y, bczzB.y)); // c
fsrEasuTapF(aC, aW, vec2(-1.0, 1.0) - P, Dir, Len, w, Clp, vec3(ijfeR.x, ijfeG.x, ijfeB.x)); // i
fsrEasuTapF(aC, aW, vec2(0.0, 1.0) - P, Dir, Len, w, Clp, vec3(ijfeR.y, ijfeG.y, ijfeB.y)); // j
fsrEasuTapF(aC, aW, vec2(0.0, 0.0) - P, Dir, Len, w, Clp, vec3(ijfeR.z, ijfeG.z, ijfeB.z)); // f
fsrEasuTapF(aC, aW, vec2(-1.0, 0.0) - P, Dir, Len, w, Clp, vec3(ijfeR.w, ijfeG.w, ijfeB.w)); // e
fsrEasuTapF(aC, aW, vec2(1.0, 1.0) - P, Dir, Len, w, Clp, vec3(klhgR.x, klhgG.x, klhgB.x)); // k
fsrEasuTapF(aC, aW, vec2(2.0, 1.0) - P, Dir, Len, w, Clp, vec3(klhgR.y, klhgG.y, klhgB.y)); // l
fsrEasuTapF(aC, aW, vec2(2.0, 0.0) - P, Dir, Len, w, Clp, vec3(klhgR.z, klhgG.z, klhgB.z)); // h
fsrEasuTapF(aC, aW, vec2(1.0, 0.0) - P, Dir, Len, w, Clp, vec3(klhgR.w, klhgG.w, klhgB.w)); // g
fsrEasuTapF(aC, aW, vec2(1.0, 2.0) - P, Dir, Len, w, Clp, vec3(zzonR.z, zzonG.z, zzonB.z)); // o
fsrEasuTapF(aC, aW, vec2(0.0, 2.0) - P, Dir, Len, w, Clp, vec3(zzonR.w, zzonG.w, zzonB.w)); // n
//------------------------------------------------------------------------------------------------------------------------------
// Normalize and dering.
return min(Max4, max(Min4, aC / aW));
}
void main()
{
ivec2 FragPos = ivec2(gl_GlobalInvocationID.xy);
imageStore(u_OutputEASUTexture, FragPos, vec4(fsrEasuF(FragPos), 1));
}
4.2 RCAS (Robust Contrast Adaptive Sharpening)
在成功用EASU进行上采样之后,FSR算法还进行了自适应锐化进一步强化边缘信息,不过相比于EASU,RCAS就十分的简单了。
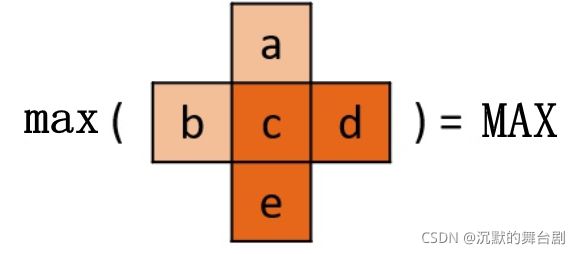
前面我们在介绍过拉普拉斯算子,RCAS就是一个拉普拉斯算子的变种,其模板为:
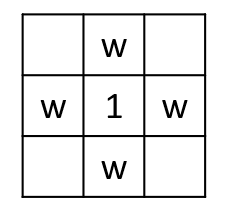
对于像素 Q 也只需要按照上面的权重计算即可:
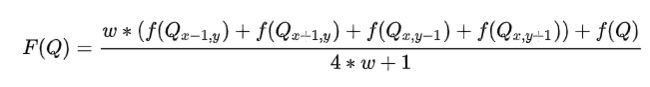
如上图所示,首先计算出最大值 Max ,以及最小值 Min :

其中 Scale 为上采样之后的分辨率与原分辨率的比值。
4.2.1 计算着色器代码
#version 430 core
#pragma optionNV (unroll all)
#define LOCAL_GROUP_SIZE 32
// This is set at the limit of providing unnatural results for sharpening.
#define FSR_RCAS_LIMIT (0.25 - (1.0 / 16.0))
layout (local_size_x = LOCAL_GROUP_SIZE, local_size_y = LOCAL_GROUP_SIZE) in;
layout (rgba32f, binding = 1) uniform writeonly image2D u_OutputRCASImage;
uniform sampler2D u_RASUTexture;
uniform vec4 u_Con0;
vec4 fsrRcasLoadF(ivec2 p) { return texelFetch(u_RASUTexture, ivec2(p), 0); }
float max3F1(float x,float y,float z){return max(x,max(y,z));}
float min3F1(float x,float y,float z){return min(x,min(y,z));}
void fsrRcasF(out float pixR,out float pixG,out float pixB,ivec2 ip) { // Constant generated by RcasSetup().
// Algorithm uses minimal 3x3 pixel neighborhood.
// b
// d e f
// h
ivec2 P = ivec2(ip);
vec3 b = fsrRcasLoadF(P + ivec2(0, -1)).rgb;
vec3 d = fsrRcasLoadF(P + ivec2(-1, 0)).rgb;
vec3 e = fsrRcasLoadF(P).rgb;
vec3 f = fsrRcasLoadF(P + ivec2(1, 0)).rgb;
vec3 h = fsrRcasLoadF(P + ivec2(0, 1)).rgb;
// Rename (32-bit) or regroup (16-bit).
float bR = b.r;
float bG = b.g;
float bB = b.b;
float dR = d.r;
float dG = d.g;
float dB = d.b;
float eR = e.r;
float eG = e.g;
float eB = e.b;
float fR = f.r;
float fG = f.g;
float fB = f.b;
float hR = h.r;
float hG = h.g;
float hB = h.b;
// Luma times 2.
float bL = bB * 0.5f + (bR * 0.5f + bG);
float dL = dB * 0.5f + (dR * 0.5f + dG);
float eL = eB * 0.5f + (eR * 0.5f + eG);
float fL = fB * 0.5f + (fR * 0.5f + fG);
float hL = hB * 0.5f + (hR * 0.5f + hG);
// Min and max of ring.
float Min4R = min(min3F1(bR, dR, fR), hR);
float Min4G = min(min3F1(bG, dG, fG), hG);
float Min4B = min(min3F1(bB, dB, fB), hB);
float Max4R = max(max3F1(bR, dR, fR), hR);
float Max4G = max(max3F1(bG, dG, fG), hG);
float Max4B = max(max3F1(bB, dB, fB), hB);
// Immediate constants for peak range.
vec2 PeakC = vec2(1.0, -1.0 * 4.0);
// Limiters, these need to be high precision RCPs.
float HitMinR = Min4R * (1.0f / (4.0f * Max4R));
float HitMinG = Min4G * (1.0f / (4.0f * Max4G));
float HitMinB = Min4B * (1.0f / (4.0f * Max4B));
float HitMaxR = (PeakC.x - Max4R) * (1.0f / (4.0f * Min4R + PeakC.y));
float HitMaxG = (PeakC.x - Max4G) * (1.0f / (4.0f * Min4G + PeakC.y));
float HitMaxB = (PeakC.x - Max4B) * (1.0f / (4.0f * Min4B + PeakC.y));
float LobeR = max(-HitMinR, HitMaxR);
float LobeG = max(-HitMinG, HitMaxG);
float LobeB = max(-HitMinB, HitMaxB);
float Lobe = max(float(-FSR_RCAS_LIMIT), min(max3F1(LobeR, LobeG, LobeB), 0.0)) * (u_Con0.x);
// Resolve, which needs the medium precision rcp approximation to avoid visible tonality changes.
float RcpL = 1.0f / (4.0f * Lobe + 1.0f);
pixR = (Lobe * bR + Lobe * dR + Lobe * hR + Lobe * fR + eR) * RcpL;
pixG = (Lobe * bG + Lobe * dG + Lobe * hG + Lobe * fG + eG) * RcpL;
pixB = (Lobe * bB + Lobe * dB + Lobe * hB + Lobe * fB + eB) * RcpL;
}
void main()
{
ivec2 FragPos = ivec2(gl_GlobalInvocationID.xy);
vec3 Color = vec3(0);
fsrRcasF(Color.r,Color.g,Color.b,FragPos);
imageStore(u_OutputRCASImage, FragPos, vec4(Color, 1));
}
低分辨率:
FSR处理后(提升一些,但效果不太好,边缘噪点也被放大,但不依赖于硬件,还行):