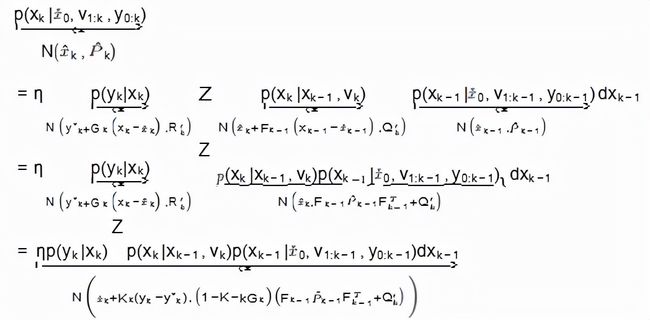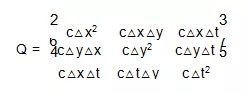©作者 | Doreen
01 问题描述
预先知道事物未来的状态总是很有价值的!
√ 预知台风的路线可以避免或减轻重大自然灾害的损失。
√ 敌国打过来的导弹,如果能够高精度预测轨迹,就能有效拦截。
√ 操控无人机,需要知道下一刻飞机的方向、速度不断修正,才能精准控制、回避各种风险。
这是一个状态估计问题
如下图所描绘的,在 k 个(一个或多个)时间点上,
基于初始的状态信息
一系列观测数据
给定控制输入
以及系统的运动和观测模型,力求预测系统在每一时刻的真实状态
以自动驾驶为例,图中符号的含义如下:
● xˇ: 设计的轨迹,比如预先计算得出的理想轨迹。
● w: 驾驶过程中各种操作引入的噪声,称为过程噪声。
● x: 在理想轨迹之上混入了过程噪声的真实轨迹。
● t 下标表示时间。
● n: 观测噪声。
● y: 观测数据:对真实轨迹的观测,其中包含观测噪声。
每一个 t − 1 时刻,系统处于
状态,输入控制信号
状态变为
这一过程用运动模型描述
此时观测到
这一个过程用观测模型描述
可以看出 t 时刻状态,在时间序列上只与 t − 1 时刻的状态有关,即具有一阶马尔科夫性。
02 EKF 算法
最开始人们对这一问题做了简化,假设模型是线性的,噪声符合高斯分布,提出了 Kalman Filter。然而总存在某些问题不符合线性与高斯假设,人们又继续探索。
2.1、Bayes Filter
由于系统状态与观测之间的因果关系,人们首先想到了贝叶斯定理。对于状态x, 由先验p(x), 后验概率 p(x|y), 推到观测对象发生的概率。
考虑到系统的马尔科夫性, t 时刻状态与 t − 1 时刻之前的状态和控制 输入都没有关系,忽略无关项,改写后如下。
2.2、算法改进
上述 Bayes Filter 是精确的模型,然而实际应用却有两个困难:
1.概率密度函数是个无穷维函数空间,需要无先的内存,置信度 p(xk|0, v1:k, y0:k) 需要近似。一般通过采样的方法解决。
2.由于积分的关系, 计算量会非常大, 一般通过将运动模型和观测模型 线性化来解决或通过蒙特卡洛积分。
有很多的科研成果聚焦在如何解决这两个问题, 代表性的如本文下面讨论 的 EKF, Particl Filter ,Sigmapoint Kalman Filter 等。另外在 Bayes Filter 近似算法中很重要一点是保持马尔科夫性。
2.3、EKF
EKF 在近似 Bayes Filter 的时候采用的近似方案是将模型线性化,假设噪声是高斯的。emmm, 捂脸,.... 说的就是因为模型非线性、噪声非高斯。
所以回到 Bayes Filter,然后 Bayes Filter 有难以克服的障碍,需要近似解,而解决方案绕一圈竟然又回到了线性高斯假设的原点,这是骗鬼呢么?
真的, 这就是著名的 EKF。在Kalman,1960发表了他的Kalman FIlter论文后, 他遇到了 NASA Ames Reserach Center 的 Stanley F.Schmidt,他们一起对 Kalman Filter 做了改进,最终应用在 NASA Apollo 项目的航空器轨迹估计上。看EKF曾经多么NB闪闪。
他们的改进主要集中在 3 个方面:
i 将原有的工作扩展到非线性模型和非高斯噪声领域。
ii 对当前最优解做线性化,以减轻非线性带来的影响。
iii 将原来的滤波器改造为现在标准的预测和校正两步。
原来的 Bayes Filter 经过线性近似和高斯假设后变为:
可以看出公式 (1.18) 与公式 (1.6) 出发点是一样的, 只是 (1.18) 给出了可 性的均值方差求解公式。
对照公式 ((1.18)) 左右两边,可以得出:
状态预测:
卡尔曼增益:
修正项
03 编程实现
3.1 几个重要的矩阵
本文只侧重 SLAM 中有关的应用。文末有示例代码链接。
首先简单介绍 EKF 中的几个重要矩阵。
3.2 系统状态矩阵 X
由机器人 robot 位姿和 n 个路标 landmank 的坐标组成的 (3 + 2 × n,1) 矩阵, 称为系统状态矩阵。
位移变量的单位可以是米或厘米,角度变量的单位是度或弧度。
3.3 协方差矩阵 P
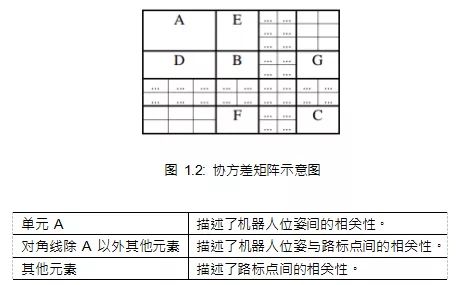
协方差矩阵 P 在 SLAM 中十分重要,描述了机器人位姿间的相关性,机器人位姿与路标间的相关性以及路标与路标间的相关性。P 是对称的。
P 矩阵是对称的,E=D,F=G(代表了最后一个路标与第一个路标的协 方差项)。在增加新的路标点的时候,不仅要在对角线上增加各自的协方差项,还要增加与机器人的协方差项 (第一行、第一列),以及与其他路标的协方差项。
矩阵内容大致如下:
协方差矩阵最初如果没有观测到路标点,会只包含 A,随着新的路标点不断加入,维度会越来越大。
考虑到初始化的不确定性,即使机器人位姿是精确的,给 A 一个合适的初值也是明智的,反之可能会在求解过程中遇到一些问题。
3.4 卡尔曼增益: K
卡尔曼增益供我们选择的机会,选择从观测路标点获取的信息和机器人自带的里程计信息哪个更可靠。
K 矩阵与状态矩阵是互相对应的,每一行代表一个状态变量。
第 1 行代表状态矩阵X第1行发生变化引起的增益,
其中
表示沿x轴位移引起的增益,
对应绕 x 轴旋转引起的增益。
第 2 行代表状态矩阵X第2行发生变化引起的增益,其中
表示沿y轴位移引起的增益,
对应绕y轴旋转引起的增益。
. . . 以此类推。
3.5 观测模型的 Jacobian 矩阵: H
机器人对路标点的观测可以表示为:
路标点坐标保存在系统状态矩阵里, 直接读取就可以:
观测模型的 Jacobian 矩阵: 路标观测向量对机器人状态估计值
的求导。
简化表示成如下形式:
具体的例子如:
如果观测的路标是
那么在
对应位置填上相反的值,
(路标没有旋转)
3.6 预测模型的 Jacobian 矩阵: A
预测模型:在给定机器人坐标和控制下预测机器人下一时刻将要到达的坐标。
其中 (x, y) 表示当前机器人坐标,△t 表示驱动的增量,q 是误差项,f 对机器人参数求导:
emmm …带 q 的误差那一被项被忽略掉了。用 △tcosθ 代替 △x,△tsinθ 代替 △y 就变成了
3.7 SLAM 中的 EKF 独有的 Jacobian
表达由机器人位置 (x, y) 引起的对路标预测误差误差
对路标的预测对路标坐标的 Jacobian
3.8 过程噪声 Q 和 W
过程噪声是与控制信号成比例的高斯噪声,记作 Q。如果
C 与里程计的准确性有关,准确性高对应的系数就大,通常是需要实验调参的。
3.9 测量噪声: R 和 V
观测噪声是与路标测量 (range,bearing)有关的 2×2 矩阵,
形如
其中 r 与 range 有关, c 是常数, 如果 range 误差 1cm, c 应该取值 0.01,表示高斯噪声方差。
如果 bearing 误差 1 度, b=1。
常数与测量设备的准确性有关。
有了上面几个关键矩阵的铺垫,下面终于 EKF 流程了:
3.10 使用里程计更新系统当前状态
更新的是状态矩阵 X(1.3.2) 前 3 个量
3.11 更新预测模型 Jacobian
3.12 更新过程噪声
过程噪声是与控制紧密相关的。
3.13 更新机器人位姿有关的协方差
(协方差矩阵顶部 3 × 3) 块。
3.14 用重新观测的路标数据更新当前状态
预测路标
仅从机器人位置信息更新状态是不够准确的,还可以通过对路 标点的重新观测修正机器人位姿。对于机器人当前位姿 (x, y) 和上一时刻路 标坐标 (λx, λy) 可以计算距离和角度 h:
还可以直接通过传感器计算路标。
3.15 更新测量误差矩阵 R, V
其中 r = range, c = 0.01, bd = 1
3.16 计算 kalman 增益
3.17 新的状态向量
3.18 把新的路标加入状态
用新的路标点更新状态向量 X
3.19 更新协方差矩阵
更新协方差矩阵 P: 对角线元素
更新协方差矩阵 P: 机器人-路标相关元素
更新协方差矩阵 P:路标-机器人相关元素
更新协方差矩阵 P:路标-路标相关元素
3.20 实验结果
图中蓝色是理想轨迹,黑色是真实轨迹,红色是估计的结果。
04 源代码地址
h t t p s : / / g i t h u b . com/Hou−a l e x / p u b l i c S r c / b l o b /main/ ekf_slam . py