多传感器融合定位 第十章 基于优化的定位方法
第十章 基于优化的定位方法
本章是基于先验地图的图优化方法,先验地图的构建可参考多传感器融合定位 第九章 基于优化的建图方法
代码下载:
1.环境配置:
出现以下问题,是由于 make_unique 是c++ 14的新特性,需要在CMakelists.txt 中添加c++14 的编译指向。参考链接
lidar_localization/src/models/sliding_window/ceres_sliding_window.cpp:25:38: error: ‘make_unique’ is not a member of ‘std’
config_.loss_function_ptr = std::make_unique<ceres::CauchyLoss>(new ceres::CauchyLoss(1.0));
解决, 在CMakelists.txt 添加
set(CMAKE_CXX_STANDARD 14)
2.因子图优化代码补充
参考博客:
因子图优化 SLAM 研究方向归纳
多传感器融合定位 第九章 基于优化的建图方法
多传感器融合定位理论基础(十二):滑动窗口原理及应用
本章因子图优化,涉及的内容较多,建议先修参考一下内容:
VINS系列相关代码:滑动窗口部分
邱笑晨博士的《预积分总结与公式推导》(发表于泡泡机器人公众号)
机器人状态估计:理论推导部分
深蓝学院《从零手写VIO》课程:滑窗和边缘话理论讲解 (重点参考)
多传感器融合定位理论基础(十二):滑动窗口原理及应用 (重点参考)
以下代码补充的公式摘自GeYao助教的手推公式,图表摘自任乾老师课上的笔记,需要补全的代码主要有两大类:
代码参考:1. GEYAO助教的github 2.张嘉皓助教的github
1.实现预积分、地图匹配、边缘化、帧间匹配四种优化因子。
2.将上述四种约束因子,加入滑窗,进行优化
2.1 实现预积分、地图匹配、边缘化、帧间匹配四种优化因子
2.1.1 激光里程计因子
a.示意图
b.激光里程计因子 残差函数和雅克比矩阵 推导
注意的是,GeYao助教的公式推导和代码少了,位置残差对姿态的雅克比,以下为补充的推导。
c.代码补全
FILE: factor_prvag_relative_pose.hpp
//
// TODO: get square root of information matrix:
//
Eigen::Matrix<double, 6, 6> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 6 ,6>>(
I_
).matrixL().transpose() ;
//
// TODO: compute residual:
//
Eigen::Map<Eigen::Matrix<double, 6 ,1>> residual(residuals); // 残差 r_P r_R
residual.block(INDEX_P, 0 , 3 , 1) = ori_i.inverse() * (pos_j - pos_i) - pos_ij ;
residual.block(INDEX_R, 0 , 3 , 1) = (ori_i.inverse()*ori_j*ori_ij.inverse()).log( );
//
// TODO: compute jacobians: 因为是二元边,所以需要求解两个jacobian
//
if ( jacobians ) {
// compute shared intermediate results:
const Eigen::Matrix3d R_i_inv = ori_i.inverse().matrix();
const Eigen::Matrix3d J_r_inv = JacobianRInv(residual.block(INDEX_R, 0 ,3 , 1)); // 右雅克比
const Eigen::Vector3d pos_ij = ori_i.inverse() * (pos_j - pos_i) ;
if ( jacobians[0] ) { // 残差rL0(rp rq ) 对 T0(p q) M0(v ba bg) 的雅克比
// implement computing:
Eigen::Map<Eigen::Matrix<double, 6 , 15, Eigen::RowMajor>> jacobian_i (jacobians[0] ); // col : rp_i[3] rq_i[3] row : p[3] q[3] v[3] ba[3] bg[3]
jacobian_i.setZero();
jacobian_i.block<3, 3>(INDEX_P, INDEX_P) = -R_i_inv;
jacobian_i.block<3, 3>(INDEX_R,INDEX_R) = -J_r_inv*(ori_ij*ori_j.inverse()*ori_i).matrix();
jacobian_i.block<3, 3>(INDEX_P,INDEX_R) = Sophus::SO3d::hat(pos_ij).matrix();
jacobian_i = sqrt_info * jacobian_i ; // 注意 sqrt_i 为对角的协方差矩阵对角线为观测的方差,可理解为传感器的测量误差,用于调整权重用
}
if ( jacobians[1] ) { // 残差rL0(rp rq ) 对 T0(p q) M0(v ba bg) 的雅克比
// implement computing:
Eigen::Map<Eigen::Matrix<double, 6 ,15, Eigen::RowMajor>> jacobian_j (jacobians[1]);
jacobian_j.setZero();
jacobian_j.block<3, 3>(INDEX_P, INDEX_P) = R_i_inv;
jacobian_j.block<3, 3>(INDEX_R,INDEX_R) = J_r_inv*ori_ij.matrix();
jacobian_j = sqrt_info * jacobian_j ;
}
}
//
// TODO: correct residual by square root of information matrix:
//
residual = sqrt_info * residual;
2.1.2 地图匹配因子
a.示意图
b.地图匹配因子 残差函数和雅克比矩阵 推导
c.代码补全
//
// TODO: get square root of information matrix:
//
// Cholesky 分解 : http://eigen.tuxfamily.org/dox/classEigen_1_1LLT.html
Eigen::Matrix<double, 6, 6> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 6, 6>>(
I_
).matrixL().transpose();
//
// TODO: compute residual:
//
Eigen::Map<Eigen::Matrix<double, 6 ,1>> residual(residuals);
residual.block(INDEX_P, 0 , 3 , 1 ) = pos - pos_prior ;
residual.block(INDEX_R,0 , 3 , 1 ) = (ori*ori_prior.inverse()).log();
//
// TODO: compute jacobians: 一元边
//
if ( jacobians ) {
if ( jacobians[0] ) {
// implement jacobian computing:
Eigen::Map<Eigen::Matrix<double, 6, 15, Eigen::RowMajor>> jacobian_prior(jacobians[0] );
jacobian_prior.setZero();
jacobian_prior.block<3, 3>(INDEX_P, INDEX_P) = Eigen::Matrix3d::Identity();
jacobian_prior.block<3, 3>(INDEX_R, INDEX_R) = JacobianRInv(
residual.block(INDEX_R, 0, 3, 1)) * ori_prior.matrix();
jacobian_prior = sqrt_info * jacobian_prior ;
}
}
//
// TODO: correct residual by square root of information matrix:
//
residual = sqrt_info * residual;
2.1.3 IMU预积分因子
a.示意图
b.IMU预积分因子 残差函数和雅克比矩阵 推导
GeYao助教的推导为基于SO3形式的推导,代码也是SO3的形式。四元数的推导部分上一章已推导完成,可参考多传感器融合定位 第九章 基于优化的建图方法
c.代码补全
//
// TODO: get square root of information matrix:
// Cholesky 分解 : http://eigen.tuxfamily.org/dox/classEigen_1_1LLT.html
Eigen::LLT<Eigen::Matrix<double,15,15>> LowerI(I_);
// sqrt_info 为上三角阵
Eigen::Matrix<double,15,15> sqrt_info = LowerI.matrixL().transpose();
//
// TODO: compute residual:
//
Eigen::Map<Eigen::Matrix<double, 15, 1>> residual(residuals);
residual.block<3, 1>(INDEX_P, 0) = ori_i.inverse().matrix() * (pos_j - pos_i - (vel_i - 0.5 * g_ * T_) * T_) - alpha_ij ;
residual.block<3, 1>(INDEX_R,0) = (Sophus::SO3d::exp(theta_ij).inverse()*ori_i.inverse()*ori_j).log();
residual.block<3, 1>(INDEX_V,0) = ori_i.inverse()* (vel_j - vel_i + g_ * T_) - beta_ij ;
residual.block<3, 1>(INDEX_A,0) = b_a_j - b_a_i ;
residual.block<3, 1>(INDEX_G,0) = b_g_j - b_g_i;
//
// TODO: compute jacobians: imu预积分的残差 对状态量的雅克比,第九章已推导
//
if ( jacobians ) {
// compute shared intermediate results:
const Eigen::Matrix3d R_i_inv = ori_i.inverse().matrix();
const Eigen::Matrix3d J_r_inv = JacobianRInv(residual.block(INDEX_R, 0 ,3 , 1)); // 右雅克比
if ( jacobians[0] ) {
Eigen::Map<Eigen::Matrix<double, 15 , 15, Eigen::RowMajor>> jacobian_i (jacobians[0] );
jacobian_i.setZero();
// a. residual, position:
jacobian_i.block<3, 3>(INDEX_P, INDEX_P) = -R_i_inv;
jacobian_i.block<3, 3>(INDEX_P, INDEX_R) = Sophus::SO3d::hat(
ori_i.inverse() * (pos_j - pos_i - (vel_i - 0.50 * g_ * T_) * T_)
);
jacobian_i.block<3, 3>(INDEX_P, INDEX_V) = -T_*R_i_inv;
jacobian_i.block<3, 3>(INDEX_P, INDEX_A) = -J_.block<3,3>(INDEX_P, INDEX_A);
jacobian_i.block<3, 3>(INDEX_P, INDEX_G) = -J_.block<3,3>(INDEX_P, INDEX_G);
// b. residual, orientation:
jacobian_i.block<3, 3>(INDEX_R, INDEX_R) = -J_r_inv*(ori_j.inverse()*ori_i).matrix();
jacobian_i.block<3, 3>(INDEX_R, INDEX_G) = -J_r_inv*(
Sophus::SO3d::exp(residual.block<3, 1>(INDEX_R, 0))
).matrix().inverse()*J_.block<3,3>(INDEX_R, INDEX_G);
// c. residual, velocity:
jacobian_i.block<3, 3>(INDEX_V, INDEX_R) = Sophus::SO3d::hat(
ori_i.inverse() * (vel_j - vel_i + g_ * T_)
);
jacobian_i.block<3, 3>(INDEX_V, INDEX_V) = -R_i_inv;
jacobian_i.block<3, 3>(INDEX_V, INDEX_A) = -J_.block<3,3>(INDEX_V, INDEX_A);
jacobian_i.block<3, 3>(INDEX_V, INDEX_G) = -J_.block<3,3>(INDEX_V, INDEX_G);
// d. residual, bias accel:
jacobian_i.block<3, 3>(INDEX_A, INDEX_A) = -Eigen::Matrix3d::Identity();
// d. residual, bias accel:
jacobian_i.block<3, 3>(INDEX_G, INDEX_G) = -Eigen::Matrix3d::Identity();
jacobian_i = sqrt_info * jacobian_i;
}
if ( jacobians[1] ) {
Eigen::Map<Eigen::Matrix<double, 15, 15, Eigen::RowMajor>> jacobian_j(jacobians[1]);
jacobian_j.setZero();
// a. residual, position:
jacobian_j.block<3, 3>(INDEX_P, INDEX_P) = R_i_inv;
// b. residual, orientation:
jacobian_j.block<3, 3>(INDEX_R, INDEX_R) = J_r_inv;
// c. residual, velocity:
jacobian_j.block<3, 3>(INDEX_V, INDEX_V) = R_i_inv;
// d. residual, bias accel:
jacobian_j.block<3, 3>(INDEX_A, INDEX_A) = Eigen::Matrix3d::Identity();
// d. residual, bias accel:
jacobian_j.block<3, 3>(INDEX_G, INDEX_G) = Eigen::Matrix3d::Identity();
jacobian_j = sqrt_info * jacobian_j;
}
}
//
// TODO: correct residual by square root of information matrix:
//
residual = sqrt_info * residual;
2.1.4 边缘化先验因子
边缘化先验因子部分,算是滑窗算法的精华部分,可参考vins的做法
a.示意图
b.边缘先验因子 残差函数和雅克比矩阵 推导
c.代码补全
地图匹配H B阵
//
// TODO: Update H:
//
// a. H_mm:
H_.block<15, 15>(INDEX_M, INDEX_M) += J_m.transpose() * J_m ;
//
// TODO: Update b:
//
// a. b_m:
b_.block<15, 1>(INDEX_M , 0) += J_m.transpose() * residuals ; // 因子图叠加
点云匹配H B阵
//
// TODO: Update H:
//
// a. H_mm:
H_.block<15, 15>(INDEX_M, INDEX_M) += J_m.transpose() * J_m;
// b. H_mr:
H_.block<15, 15>(INDEX_M, INDEX_R) += J_m.transpose()* J_r;
// c. H_rm:
H_.block<15, 15>(INDEX_R, INDEX_M) += J_r.transpose() * J_m;
// d. H_rr:
H_.block<15, 15>(INDEX_R, INDEX_R) += J_r.transpose() * J_r;
//
// TODO: Update b:
//
// a. b_m:
b_.block<15, 1>(INDEX_M, 0) += J_m.transpose() * residuals ;
// a. b_r:
b_.block<15, 1>(INDEX_R, 0) += J_r.transpose() * residuals ;
IMU预积分H阵 B阵
//
// TODO: Update H:
//
// a. H_mm:
H_.block<15, 15>(INDEX_M, INDEX_M) += J_m.transpose() * J_m;
// b. H_mr:
H_.block<15, 15>(INDEX_M, INDEX_R) += J_m.transpose()* J_r;
// c. H_rm:
H_.block<15, 15>(INDEX_R, INDEX_M) += J_r.transpose() * J_m;
// d. H_rr:
H_.block<15, 15>(INDEX_R, INDEX_R) += J_r.transpose() * J_r;
//
// TODO: Update b:
//
// a. b_m:
b_.block<15, 1>(INDEX_M, 0) += J_m.transpose() * residuals ;
// a. b_r:
b_.block<15, 1>(INDEX_R, 0) += J_r.transpose() * residuals ;
边缘化操作 (核心代码)
此部分代码主要参考自vins部分
void Marginalize(
const double *raw_param_r_0
) {
// TODO: implement marginalization logic
// save x_m_0
Eigen::Map<const Eigen::Matrix<double, 15 , 1>> x_0(raw_param_r_0);
x_0_ = x_0 ;
// marginalize
const Eigen::MatrixXd &H_mm = H_.block<15, 15>(INDEX_M, INDEX_M);
const Eigen::MatrixXd &H_mr = H_.block<15, 15>(INDEX_M,INDEX_R);
const Eigen::MatrixXd &H_rm = H_.block<15, 15>(INDEX_R,INDEX_M);
const Eigen::MatrixXd &H_rr = H_.block<15, 15>(INDEX_R,INDEX_R);
const Eigen::VectorXd &b_m = b_.block<15, 1>(INDEX_M, 0);
const Eigen::VectorXd &b_r = b_.block<15, 1>(INDEX_R, 0);
Eigen::MatrixXd H_mm_inv = H_mm.inverse();
Eigen::MatrixXd H_marginalized = H_rr - H_rm * H_mm_inv * H_mr ;
Eigen::MatrixXd b_marginalized = b_r - H_rm * H_mm_inv * b_m ;
// 线性化残差 和 雅克比
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(H_marginalized);
Eigen::VectorXd S = Eigen::VectorXd(
(saes.eigenvalues().array() > 1.0e-5).select(saes.eigenvalues().array(), 0)
);
Eigen::VectorXd S_inv = Eigen::VectorXd(
(saes.eigenvalues().array() > 1.0e-5).select(saes.eigenvalues().array().inverse(), 0)
);
Eigen::VectorXd S_sqrt = S.cwiseSqrt();
Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
// finally:
J_ = S_sqrt.asDiagonal() * saes.eigenvectors().transpose(); // b0
e_ = S_inv_sqrt.asDiagonal() * saes.eigenvectors().transpose() * b_marginalized; // eo
}
关于函数SelfAdjointEigenSolver的解析(1.摘自 张嘉皓助教)(2.摘自游博的知乎)
1.由于每次迭代需要使用奇异值分解,从边缘化后的信息矩阵中恢复出来雅克比矩阵 linearized_jacobians 和残差 linearized_residuals ,这两者会作为先验残差带入到下一轮的先验残差的雅克比和残差的计算当中去。这一部分和vins是差不多的,如果看不懂的可以去 vins 那边参考参考。其中推导部分相对比较简单,如图片所示
2.游博知乎解释-更新先验残差
计算边缘因子传递的残差
//
// TODO: compute residual:
//
Eigen::Map<Eigen::Matrix<double, 15, 1>> residual(residuals);
residual = e_ + J_ * dx ; // e_prior
计算边缘因子传递的雅克比
//
// TODO: compute jacobian:
//
if ( jacobians ) {
if ( jacobians[0] ) {
// implement computing:
Eigen::Map<Eigen::Matrix<double, 15, 15, Eigen::RowMajor>> jacobian_marginalization(jacobians[0]);
jacobian_marginalization.setZero();
jacobian_marginalization = J_ ;
}
}
2.2 将四种约束因子,加入滑窗,进行优化
2.2.1 更新状态量
FILE : param_prvag.hpp
//
// TODO: evaluate performance penalty of applying exp-exp-log transform for each update
//
ori_plus = (Sophus::SO3d::exp(ori) * Sophus::SO3d::exp(d_ori)).log();
vel_plus = vel + d_vel;
b_a_plus = b_a + d_b_a;
b_g_plus = b_g + b_g_plus;
2.2.2 将因子添加到优化框架中
FILE : sliding_window.cpp
//
// add node for new key frame pose:
//
// fix the pose of the first key frame for lidar only mapping:
if ( sliding_window_ptr_->GetNumParamBlocks() == 0 ) {
// TODO: add init key frame
sliding_window_ptr_->AddPRVAGParam(current_key_frame_, true);
} else {
// TODO: add current key frame
sliding_window_ptr_->AddPRVAGParam(current_key_frame_, false);
}
// TODO: add constraint, GNSS position:
sliding_window_ptr_->AddPRVAGMapMatchingPoseFactor(
param_index_j,
prior_pose, measurement_config_.noise.map_matching
);
// a. lidar frontend:
//
// get relative pose measurement:
Eigen::Matrix4d relative_pose = (last_key_frame_.pose.inverse() * current_key_frame_.pose).cast<double>();
// TODO: add constraint, lidar frontend / loop closure detection:
sliding_window_ptr_->AddPRVAGRelativePoseFactor(
param_index_i, param_index_j,
relative_pose, measurement_config_.noise.lidar_odometry
);
//
// b. IMU pre-integration:
//
if ( measurement_config_.source.imu_pre_integration ) {
// TODO: add constraint, IMU pre-integraion:
sliding_window_ptr_->AddPRVAGIMUPreIntegrationFactor(
param_index_i, param_index_j,
imu_pre_integration_
);
}
2.2.3 ceres 中添加残差块
FILE : ceres_sliding_window.cpp
创建问题
// TODO: create new sliding window optimization problem:
ceres::Problem problem;
添加待优化参数快
// TODO: add parameter block: 添加待优化的参数快
problem.AddParameterBlock(target_key_frame.prvag, 15, local_parameterization);
if( target_key_frame.fixed ) {
problem.SetParameterBlockConstant(target_key_frame.prvag);
}
添加边缘先验因子残差块
// add marginalization factor into sliding window
problem.AddResidualBlock(
factor_marginalization,
NULL,
key_frame_r.prvag // 一元边
);
添加地图匹配因子残差块
// TODO: add map matching factor into sliding window
problem.AddResidualBlock(
factor_map_matching_pose,
NULL, // loss_function
key_frame.prvag // 一元边
);
添加帧间点云匹配匹配因子残差块
// TODO: add relative pose factor into sliding window
problem.AddResidualBlock(
factor_relative_pose,
NULL, // loss_function
key_frame_i.prvag, key_frame_j.prvag // 二元边
);
添加IMU预积分因子残差块
// TODO: add IMU factor into sliding window
problem.AddResidualBlock(
factor_imu_pre_integration,
NULL, // loss_function
key_frame_i.prvag, key_frame_j.prvag // 二元边
);
3. evo 评估
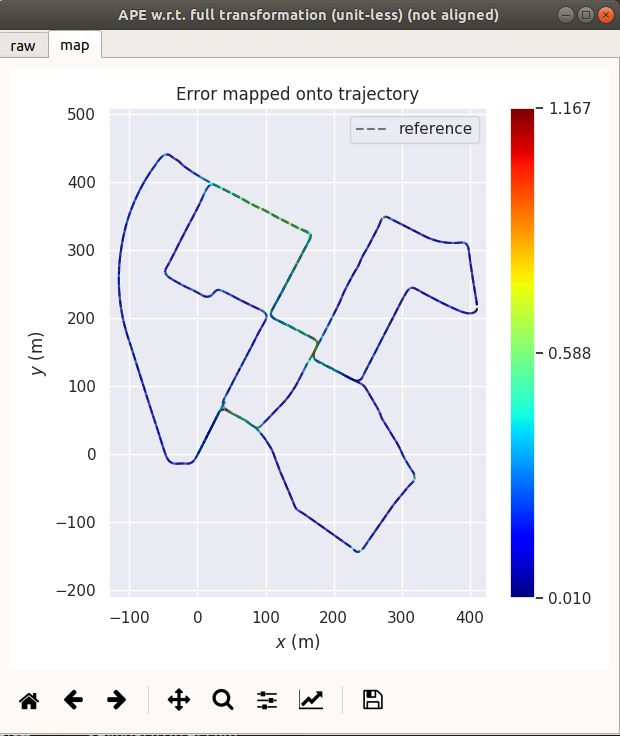
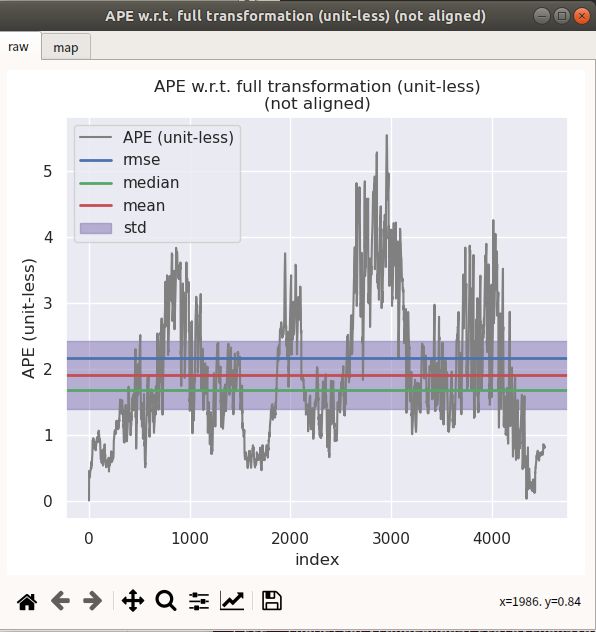
evo_ape kitti ground_truth.txt optimized.txt -r full --plot --plot_mode xyz
3.1 EKF 与 因子图优化方法比较
结果:EKF的效果暂时来看要比图优化的效果要好,但是这不一定说明图优化的效果不好,原因是KITTI数据集自身也存在一定的问题,并且在这次对比实验中,EKF 和 factor graph 所使用的先验地图构建方法不一样,EKF 使用第四章的激光里程计mapping,而factor graph 使用的是第九章imu预积分图优化的方法构建的地图。
3.2不同滑窗长度比较
FILE : lidar_localization/config/matching/sliding_window.yaml
修改不同的滑窗长度
# sliding window size:
#
sliding_window_size: 20 #滑窗长度为20帧
| sliding windows length | 2 | 10 | 15 | 20 | 30 | 地图 |
|---|---|---|---|---|---|---|
| max | 5.590900 | 5.590900 | 5.546784 | 5.510841 | 8.340555 | 2.325375 |
| mean | 2.345147 | 2.26939 | 1.907476 | 1.886341 | 2.906110 | 0.801601 |
| median | 2.178942 | 2.111248 | 1.682371 | 1.718590 | 2.988234 | 0.701903 |
| min | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.023720 |
| rmse | 2.648810 | 2.531902 | 2.167268 | 2.143079 | 3.207210 | 0.928723 |
| sse | 31769.338233 | 29026.859453 | 21268.254731 | 20796.134607 | 46452.465579 | 1650.013734 |
| std | 1.231456 | 1.122670 | 1.028876 | 1.017106 | 1.356733 | 0.469001 |
总结:
1.滑动窗口的长度也是一个关键的因素,过高或者过低的窗口长度会造成精度的降低。
2.按照乾哥的说法EKF的滤波方法就相当于滑动窗口为1的情况,可以看出,选取适当滑窗大小是有必要的,能够直接影响最后的性能。
4. 注意
sqrt_info 的理解
在求解图优化因子雅克比、残差的过程中,都会乘以一个sqrt_info 矩阵,代码的写法是参考vins,以下参考博客均有对sqrt_info 矩阵的理解
Eigen::LLT<Eigen::Matrix<double,15,15>> LowerI(I_);
// sqrt_info 为上三角阵
Eigen::Matrix<double,15,15> sqrt_info = LowerI.matrixL().transpose();
1.vins 的margin factor
2.后端优化 | VINS-Mono 论文公式推导与代码解析分讲
综上个人理解:在高斯牛顿法优化中, 非线性优化的式子为 J^T (W^-1) J = -J^T (W^-1) r,其中W为观测的协方差矩阵,为对角矩阵,对角线的每个元素为该残差的方差,即可理解为观测误差(传感器的噪声)。将W求逆即为残差的信息矩阵,可理解为权重矩阵,用于调整不同的残差项的权重(具有归一化的意义) 。因为ceres 只接受 min(e^T e ) 形式的最小二乘优化形式,所以可以通过cholesy分解的方式将残差的信息矩阵(W^-1)分解为上下三角形式,然后分别乘到残差和雅克比上,其形式与原高斯牛顿法的等式等价,相当于在把残差的信息矩阵开根号,然后分别乘到雅克比和残差上。
// 雅克比 乘 上 sqrt(残差信息矩阵)
jacobian_i = sqrt_info * jacobian_i;
// 残差 乘 上 sqrt(残差信息矩阵)
residual = sqrt_info * residual;
右乘BCH及其求逆公式
此处部分为课程中较多争议的一个部分,为扰动模型中,右雅克比在代码上的实现,摘抄自陈皓嘉助教的“第十章思路讲解”。
FILE : factor_prvag_imu_pre_integration factor_prvag_map_matching_pose factor_prvag_marginalization
// 右雅克比的逆
static Eigen::Matrix3d JacobianRInv(const Eigen::Vector3d &w) {
Eigen::Matrix3d J_r_inv = Eigen::Matrix3d::Identity();
double theta = w.norm();
if ( theta > 1e-5 )
{
Eigen::Vector3d a = w.normalized();
Eigen::Matrix3d a_hat = Sophus::SO3d::hat(a);
double theta_half = 0.5 * theta ;
double cot_theta = 1.0 / tan(theta_half);
J_r_inv = theta_half * cot_theta * J_r_inv + (1.0 -
theta_half * cot_theta) * a * a.transpose() +
theta_half * a_hat ;
}
return J_r_inv;
}
关于是否需要添加帧间里程计因子的讨论
摘自学员解答:
由于我们播的是相同的数据集,点云地图匹配和激光里程计的结果差不多,如果地图变化比较大,激光里程计的存在会使系统更加鲁棒。
5. 课程答疑总结
5.1 进行舒尔补构建b矩阵是,正负号问题
答:公式上是没问题的,区别在于构建残差是是 (预测-观测) or (观测-预测)
5.2 因子图优化中Ti Tj 问题
问:我有个疑问,这里添加的因子是,激光里程计因子,是点云的scan2scan, 作残差时,是这两帧通过点云匹配相对位姿 Tij 和 Ti Tj计算的相对位姿比较,这里没有矛盾么,因为这里的因子是点云匹配出来的,而Ti Tj 一开始也是点云匹配给的,在做残差时,不相当于自己减自己?
Ti Tj 一般是预测值,一般是由scan2scan 上一时刻的后验POSE给的后验,作为预测。残差模型一般都是遵循 (观测 - 预测)模式,scan2map 先验地图匹配一般不作为先验因子,一般作为观测量。
5.3 EKF 与 factor graph 对比
问:因子图优化对比EKF在工程上的优势,因为我在第十章EKF 和 因子图对比中,发现EKF的效果要好点。
答:在课程的效果中,EKF 对比 因子图优化的效果要好,鉴于数据集本身存在分米级的误差,所以不用太在意。实际上,因子图优化开始取代EKF。在建图领域,大部分都使用优化的方法,在定位,目前大多数还是kalman的方法,包括apollo也是沿用kalman的定位方案,但是优化方法也在逐步取代。优化方法体现的优势在于:EKF的方法基于一阶马尔科夫性,只是局部最优,而图优化的方法是基于全局最优,即使是滑窗方法上的优化方法,也是选取多帧最优。
5.4 scan2map中的map
问:因子图优化中的激光里程计约束指的scan2scan 还是 scan2map, 如果是scan2map 的话,那它和“先验地图匹配因子”的区别是在于 “激光里程计因子”的map是局部分割的小地图,“先验地图匹配因子”的map是大地图是吗? 使用全局的大地图匹配,对资源消耗不是很大吗?
答:激光里程计:前端激光里程计主要还是loam的方案,使用的是scan2map 方式构建,这里的map并不是只小的先验地图,只是指loam里的submap小特征地图。“先验地图匹配因子”里所说的先验地图,使用滑窗分割出的小地图,为了节省运算资源。
5.5 如何去评估地图的质量精度
a.使用更高精度的惯性传感器,进行建图时的轨迹评估;
b.标志物评判,实地选取一个标志物,使用RTK去测量当地标志物的经纬高,对应地图上同一个标志物,计算误差,多取几个,可以构建出误差系数。
5.6 slam中GPS的主要作用
gps的主要作用个人认为主要有两个:1.消除行驶过程中累积误差; 2.室外重定位过程中的初始化有很大作用。
5.7 点云匹配过程中,特征退化的现象(长廊、隧道),有什么方法可以判断出来?(待补充)
1.特征退化的场景(如长廊、隧道),因为只有两侧的观测,可以对匹配的协方差矩阵进行特征值分解,通过判断特征值的分布状况判断。
2.也可已增加imu uwb等辅助传感器。
5.8 IMU上电的bias需要怎么估计?(待补充)
kitti数据集中貌似已估
5.9 图优化 因子图 位姿图 概念(待补充)
5.10 SLAM 算法岗位应届生招聘要求
a.slam 的基础知识,前端匹配:icp ndt, 后端优化: 高斯牛顿法、LM优化
b.代码能力(leetcode top 100 、 剑指offer)
c.常见的开源框架, 优点(为什么选择他) ,缺点(如何改进)
d.项目经验(重点): 为什么这样搞,这样搞的好处、优势。
edited by kaho 2022.3.19