位运算详解与其用途
1.位运算起源
位运算起源于C语言的低级操作,Java的设计初衷是嵌入到电视机顶盒内,所以这种低级操作方式被保留下来。所谓的低级操作,是因为位运算的操作对象是二进制位,但是这种低级操作对计算机而言是非常简单直接,友好高效的。在简单的低成本处理器上,通常位运算比除法快得多,比乘法快几倍,有时比加法快得多。虽然由于较长的指令流水线和其他架构设计选择,现代处理器通常执行加法和乘法的速度与位运算一样快,但由于资源使用减少,位运算通常会使用较少的功率,所以在一些Java底层算法中,巧妙的使用位运算可以大量减少运行开销。
2、 位运算详解
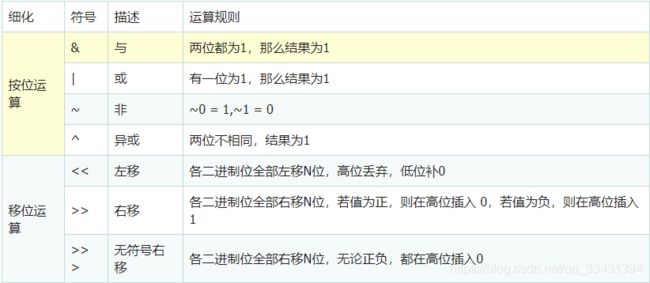
Java位运算细化划分可以分为按位运算和移位运算,见下表。
在进行位运算详解之前,先来普及下计算机中数字的表示方法。对于计算机而言,万物皆0、1,所有的数字最终都会转换成0、1的表示,有3种体现形式,分别是:原码、反码和补码。
- 原码:原码表示法在数字前面增加了一位符号位,即最高位为符号位,正数位该位为0,负数位该位为1.
比如十进制的5如果用8个二进制位来表示就是00000101,-5就是10000101。
- 反码:正数的反码是其本身,负数的反码在其原码的基础上,符号位不变,其余各个位取反。
5的反码就是00000101,而-5的则为11111010。
- 补码:正数的补码是其本身,负数的补码在其原码的基础上,符号位不变,其余各位取反,最后+1。
即在反码的基础上+1。5的反码就是00000101,而-5的则为11111011。
2.1 与运算(&)
规则:转为二进制后,两位为1,则结果为1,否则结果为0。
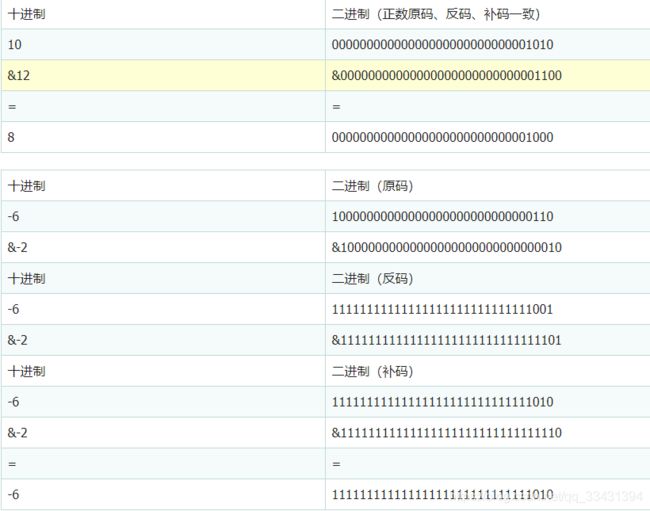
最后的计算结果11111111111111111111111111111010还是补码的形式,要看其十进制,还需要先转成二进制原码。
先转反码:11111111111111111111111111111010-1=11111111111111111111111111111001,得反码11111111111111111111111111111001。
再转原码:在反码的基础上转原码,符号位不变,其他各位取反,得10000000000000000000000000000110。第一位1代表负数,后面0110转成十进制是6,得-6。
2.2 或运算(|)
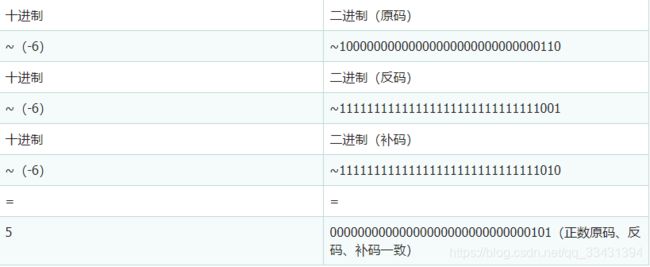
2.3 非运算(~)
规则:转为二进制后,~0 = 1,~1 = 0。
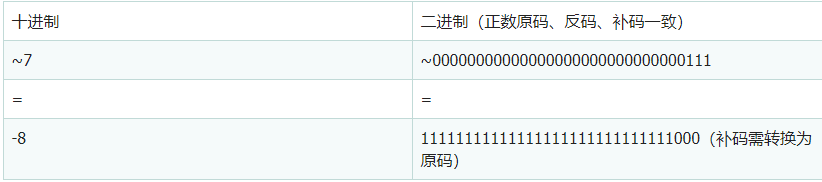
11111111111111111111111111111000-1得反码,可以把1000看成是0112,得反码
11111111111111111111111111110111。根据反码得原码10000000000000000000000000001000。
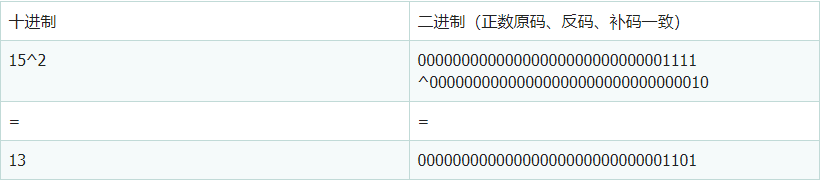
2.4 异或运算(^)
2.5 左移运算(<<)
规则:转为二进制后,各二进制位全部左移N位,高位丢弃,低位补0。

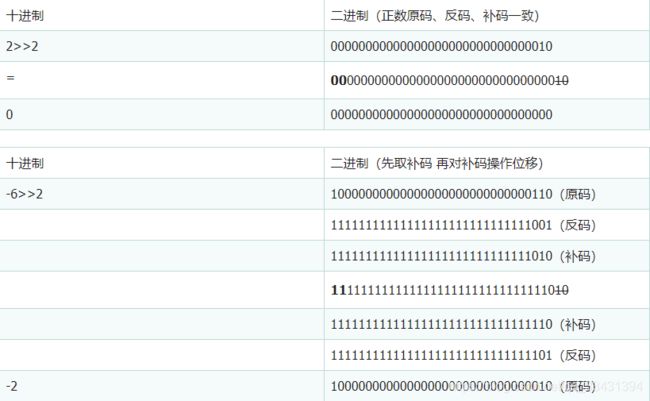
2.6 右移运算(>>)
规则:转为二进制后,各二进制位全部右移N位,若值为正,则在高位插入 0,若值为负,则在高位插入 1。
2.7 无符号右移运算(>>>)
规则:转为二进制后,各二进制位全部右移N位,无论正负,都在高位插入0。

3.用途
3.1. 对称加密
其实现原理是一个数异或同一个数两次还是原数
public static String encode(String source, int key) {
byte[] b = source.getBytes("UTF-8");
for (int i=0, size=b.length; i<size; i++) {
for (byte keyBytes0 : keyBytes) {
b[i] = (byte) (b[i]^key);
}
}
return new String(b);
}
如上代码可以将 source 字符串加密成一个新串,解密时将加密过的字符串还用上面方法传给 source 即可得到加密前的字符串,这样就成了用 key 实现的对称加密。
3.2. 乘除幂运算
//计算n*2
int mulTwo(int n) {
return n << 1;
}
//除以2,负奇数的运算不可用
int divTwo(int n) {
return n >> 1;//除以2
}
//计算n*(2^m),即乘以2的m次方
int mulTwoPower(int n,int m) {
return n << m;
}
//计算n/(2^m),即除以2的m次方
int divTwoPower(int n,int m) {
return n >> m;
}
3.3. 奇偶判断
//判断数值的奇偶性
boolean isOddNumber(int n){
return (n & 1) == 1;
}
3.4. 不增加新变量的情况下交换两个变量的值
//常规交换方式
int temp;
temp = a;
a = b;
b = temp;
//基于位运算的方式
a = a ^ b;
b = a ^ b; //实际上是(a^b)^b,也就是a异或了b两次,等号右边是a的值。
a = a ^ b;
3.5. 十进制转十六进制
public static String decimalToHex(int decimal) {
String hex = "";
while (decimal != 0) {
int hexValue = decimal % 16;
hex = toHexChar(hexValue) + hex;
decimal = decimal / 16;
}
return hex;
}
//将0~15的十进制数转换成0~F的十六进制数
public static char toHexChar(int hexValue) {
if(hexValue <= 9 && hexValue >= 0) {
return (char)(hexValue + '0');
} else {
return (char)(hexValue - 10 + 'A');
}
}
3.6 求平均数
求平均值,比如有两个int类型变量x、y,首先要求x+y的和,再除以2,但是有可能x+y的结果会超过int的最大表示范围,所以位运算就派上用场啦。
(x&y)+((x^y)>>1);
Java 位运算妙用
位运算