高斯过程回归的权空间观点推导及代码实现

1.高斯过程简介

1.1定义

高斯过程是随机变量的集合，其中任意有限个随机变量具有联合高斯分布。

在函数空间(function-space view)的观点中，高斯过程可以看作是一个定义在函数上的分布，并且直接在函数空间中进行inference。

与之等价的观点是权空间观点(weight-space view)，在权空间中进行推断,对权向量的不同抽样将产生不同的函数，这与函数空间观点是一致的,但是函数空间的观点更为直接和抽象。

注 :为方便起见，本文不刻意区分概率密度和概率质量函数，向量用小写字母如$x$表示，矩阵用大写字母如$X$表示，标量将作特别说明。

2.部分基础知识（已具备的直接跳至第3节）

2.1 部分矩阵计算基础

2.1.1 分块矩阵求逆

感兴趣可看推导过程，否则直接看最后结论。

设矩阵
$$\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$$
为可逆矩阵，下面求该矩阵的逆（推导是逆矩阵存在的假设下进行）。

设
$$\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)\left(\begin{array}{c}X\\ Y\end{array}\right)=\left(\begin{array}{c}P\\ Q\end{array}\right)$$,
可得
$$\{\begin{array}{l}AX+BY=P\dots \dots (1)\\ CX+DY=Q\dots \dots (2)\end{array}$$
由$(2)$可得，$$Y=D^{-1}(Q-CX)\dots \dots (3)$$
将$(3)$带入(1)并移项整理可得，
$$X=(A-B{D}^{-1}C{)}^{-1}(P-B{D}^{-1}Q)\dots \dots (4)$$
将$(4)$带入$(3)$整理可得,
$$Y=D^{-1}(Q-C(A-B{D}^{-1}C{)}^{-1}(P-B{D}^{-1}Q))$$
令$M=(A-B{D}^{-1}C{)}^{-1}$，其实$M$就是关于$D$的舒尔补(The Shur complements)。

分别令
$$\{\begin{array}{l}P=I\\ Q=0\end{array}及\{\begin{array}{l}P=0\\ Q=I\end{array}$$
其中$I$为单位矩阵。
可得原分块矩阵的逆矩阵
$$\left(\begin{array}{cc}M& -MB{D}^{-1}\\ -D^{-1}CM& D^{-1}+D^{-1}CMB{D}^{-1}\end{array}\right)\dots \dots (5)$$

2.1.2 矩阵求逆引理

$$(A+BCD{)}^{-1}=A^{-1}-A^{-1}B(I+CD{A}^{-1}B{)}^{-1}CD{A}^{-1}\dots \dots (6)$$
其中矩阵$A$可逆。
证明：

$设(A+BCD)X=I$，其中$I$为单位矩阵，则可得
$$\{\begin{array}{l}AX+BY=I\dots \dots (7)\\ Y=BCX\dots \dots (8)\end{array}$$
由$(7)$可得$X=A^{-1}(b-BY)$，并带入$(8)$整理得
$$Y=(I+CD{A}^{-1}B{)}^{-1}CD{A}^{-1}$$
回代得到
$$X=A^{-1}-A^{-1}B(I+CD{A}^{-1}B{)}^{-1}CD{A}^{-1}$$

2.2 多元高斯分布

2.2.1 联合分布

设$x$是一个$n$维向量,则其概率密度函数是
$$p(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}{\left|\begin{array}{c}\Sigma \end{array}\right|}^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\}\dots \dots (9)$$

其中,$\Sigma$和$\mu$分别是随机向量$x$的协方差矩阵和均值向量。

多维高斯分布具有非常良好的性质：

1. 边缘分布满足高斯分布。
2. 条件分布满足高斯分布。
3. 各分量的线性组合也是高斯随机变量。

2.2.2 条件概率分布

设随机向量$x$符合多维高斯分布，将其分为不相交的两部分
$$x=\left(\begin{array}{c}{x}_a\\ x_b\end{array}\right)$$，

$x$的均值向量
$$\mu =\left(\begin{array}{c}{\mu }_a\\ {\mu }_b\end{array}\right)$$
协方差矩阵为
$$\Sigma =\left(\begin{array}{cc}{\Sigma }_{aa}& {\Sigma }_{ab}\\ {\Sigma }_{ba}& {\Sigma }_{bb}\end{array}\right)$$
精度矩阵为
$$\Lambda ={\Sigma }^{-1}=\left(\begin{array}{cc}{\Lambda }_{aa}& {\Lambda }_{ab}\\ {\Lambda }_{ba}& {\Lambda }_{bb}\end{array}\right)$$
其中协方差矩阵是正定的，因为其对称性，${\Sigma }_{ab}={\Sigma }_{ab}^T$，${\Lambda }_{ab}={\Lambda }_{ab}^T$。

注意这是分块矩阵，不能对每个矩阵块简单求逆，我们使用公式$(5)$，可得
$${\Lambda }_{aa}=({\Sigma }_{aa}-{\Sigma }_{ab}{\Sigma }_{bb}^{-1}{\Sigma }_{ba}{)}^{-1}\dots \dots (10)$$

$${\Lambda }_{ab}=-({\Sigma }_{aa}-{\Sigma }_{ab}{\Sigma }_{bb}^{-1}{\Sigma }_{ba}{)}^{-1}{\Sigma }_{ab}{\Sigma }_{bb}^{-1}\dots \dots (11)$$

接下来，我们求在给定$x_b$的条件下，$x_a$的条件概率分布。注意到高斯分布的形式主要取决于指数项，因此我们使用配方法来找出相应的均值和协方差矩阵，而不需要考虑归一化系数，就可以得到条件分布的形式。

指数项为
$$-\frac{1}{2}(x_a-{\mu }_a{)}^T{\Lambda }_{aa}(x_a-{\mu }_a)-\frac{1}{2}(x_a-{\mu }_a{)}^T{\Lambda }_{ab}(x_b-{\mu }_b)-\frac{1}{2}(x_b-{\mu }_a{)}^T{\Lambda }_{ba}(x_a-{\mu }_a)-\frac{1}{2}(x_b-{\mu }_b{)}^T{\Lambda }_{bb}(x_b-{\mu }_b)\dots (12)$$
观察式(9)中指数项的形式，可发现精度矩阵出现在$x$的二次项中，精度矩阵和均值的乘积出现在$x^T$的线性项中，因此我们可得
$$\begin{gathered} {\Sigma }_{a|b}={\Lambda }_{aa}^{-1}\dots \dots (13) \\ {\Lambda }_{ab}{\mu }_{a|b}={\Lambda }_{aa}{\mu }_a-{\Lambda }_{ab}(x_b-{\mu }_b)\dots \dots (13^{\prime }) \end{gathered}$$
由式(10)(11)可得
$${\mu }_{a|b}=({\mu }_a-{\Lambda }_{aa}^{-1}{\Lambda }_{ab}(x_b-{\mu }_b))\dots \dots (14)$$
这样我们就得到了$p(x_a|x_b)$的分布，我们发现它的协方差是不依赖与$x_b$的，而均值是$x_b$的线性函数，这实际上是线性高斯模型的一个例子。

2.2.3 简单的线性高斯模型及贝叶斯定理

贝叶斯公式：
$$p(x|y)=\frac{p(x)p(y|x)}{p(y)}\dots \dots (15)$$
我们设
$$\begin{gathered} x\sim Gaussian(x|\mu ,{\Lambda }^{-1}) \\ y|x\sim Gaussian(y|Ax+b,L^{-1}) \end{gathered}$$
其中$\Lambda 和L$为$x和y$的精度矩阵，$y$的均值为$x$的线性函数。
接下来，我们想要知道$z=\left(\begin{array}{c}x\\ y\end{array}\right)$的联合分布。

依然使用配方的方法，关注于指数项的系数。根据式(15)可得，
$$lnp(z)\propto lnp(x)+lnp(y|x)$$
因此观察
$$-\frac{1}{2}(x-\mu {)}^T\Lambda (x-\mu )-\frac{1}{2}(y-Ax-b{)}^{T}L(y-Ax-b)$$
整理二次项，有
$$\begin{gathered} -\frac{1}{2}{x}^T(\Lambda +A^{T}LA)x-\frac{1}{2}{y}^{T}Ly+\frac{1}{2}{y}^{T}LAx+\frac{1}{2}{x}^T{A}^{T}Ly \\ =-\frac{1}{2}\left(\begin{array}{cc}{x}^T& y^T\end{array}\right)\left(\begin{array}{cc}\Lambda +A^{T}LA& A^{T}L\\ LA& L\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right) \end{gathered}$$
因此可得精度矩阵
$$R[z]=\left(\begin{array}{cc}\Lambda +A^{T}LA& A^{T}L\\ LA& L\end{array}\right)\dots (16)$$
根据公式(5)可得协方差矩阵，
$$Cov[z]=\left(\begin{array}{cc}{\Lambda }^{-1}& {\Lambda }^{-1}{A}^T\\ A{\Lambda }^{-1}& L^{-1}+A{\Lambda }^{-1}{A}^T\end{array}\right)\dots (17)$$
再观察一次项
$$x^T\Lambda \mu -x^T{A}^{T}Lb+y^{T}Lb={\left(\begin{array}{c}x\\ y\end{array}\right)}^T\left(\begin{array}{c}\Lambda \mu -A^{T}Lb\\ Lb\end{array}\right)$$
由此并根据式(13’)(16)可得均值
$$E[z]=\left(\begin{array}{c}\mu \\ A\mu +b\end{array}\right)\dots \dots (18)$$
这个结果也是符合我们的直觉的，由此可得$y$的边缘分布为
$$\begin{gathered} E[y]=A\mu +b\dots \dots (19) \\ Cov[y]=L^{-1}+A{\Lambda }^{-1}{A}^T\dots \dots (20) \end{gathered}$$

3.高斯过程回归的权空间观点推导

首先回想一般的线性回归模型，我们先不引入基函数，
$$y=x^{T}w+ϵ$$
其中$y,epsilon$是一维变量，代表实际数据值，$ϵ$表示高斯噪声，我们假设
$$ϵ\sim Gaussian(ϵ|0,{\sigma }_n^2)$$
因此，由于训练样本$x$是确定量，则
$$y|w,x\sim Gaussian(y|x^{T}w,{\sigma }_n^2)$$
下面规定$Y$为实际数据值组成的向量，$X$为输入$x$组成的矩阵，这里我们反常的规定$X$的每一列为一个输入，样本为
$$\{(x_i,y_i),i=1,2,\dots n\},其中x_i为N维向量$$
我们先做出$w$的先验分布假设，设
$$w\sim Gaussian(w|0,{\Sigma }_p)\dots \dots (21)$$
Y的似然函数为
$$p(Y|w,X)=\prod _i^{n}p(y_i|w,x_i)=Gaussian(Y|X^{T}w,{\sigma }_n^{2}I)\dots \dots (22)$$
根据贝叶斯定理以及式(19)(20)可得$w$的后验分布
$$w|Y,X\sim Gaussian(w|{\sigma }_n^{-2}{A}^{-1}XY,A^{-1})$$
$$其中A={\Sigma }_p^{-1}+{\sigma }_n^{-2}X{X}^T$$

得到$w$的后验分布之后，我们需要进行预测，即得到预测分布，给定测试样本$(X_{\ast },Y_{\ast })$，我们仍考虑测试样本点带有高斯噪声的情况。从根本上来说，我们最终想得到的不是带有噪声的样本值，而是得到生成这些数据的函数，这也符合定义中所述：高斯过程是一个定义在函数上的分布。假设预测的函数为$f_{\ast }$，
则
$$p(f_{\ast }|X_{\ast },X,Y)=\int p(f_{\ast }|X_{\ast },w)p(w|X,Y)dw$$
$$f_{\ast }|X_{\ast },w\sim Gaussian(f_{\ast }|X_{\ast }^{T}w,{\sigma }_n^{2}I)$$
这同样是一个线性高斯模型，我们需要求解边缘概率分布，由式(19)(20)可得
$$f_{\ast }|X_{\ast },X,Y\sim Gaussian(f_{\ast }|{\sigma }_n^{-2}{X}_{\ast }^T{A}^{-1}XY,X_{\ast }^T{A}^{-1}{X}_{\ast })$$
其中
$$A={\Sigma }_p^{-1}+{\sigma }_n^{-2}X{X}^T$$
接下来，我们引入基函数，用基函数$\varphi (.)$将样本输入$x_i$映射到高维特征空间，用$\varphi (x_i)或{\varphi }_i$来表示映射后的特征向量(feature vector，与eigenvector区分)，用$\Phi$表示特征向量组成的矩阵。
则
$$f_{\ast }|X_{\ast },X,Y\sim Gaussian(f_{\ast }|{\sigma }_n^{-2}{\Phi }_{\ast }^T{A}^{-1}XY,{\Phi }_{\ast }^T{A}^{-1}{\Phi }_{\ast })\dots \dots (23)$$
其中
$$A={\Sigma }_p^{-1}+{\sigma }_n^{-2}\Phi {\Phi }^T\dots \dots (24)$$
但是显示表示一个合适的基函数(basis function)不是一件容易的事情，更别说加上一个先验的协方差矩阵，因此我们隐式的引入这一式子。

我们设$K={\Phi }^T{\Sigma }_p\Phi$，我们先对式(24)进行处理。
等式两边同时左乘$A^{-1}$，右乘${\Sigma }_p\Phi$,进行整理并带入$K$可得
$$A^{-1}\Phi ={\sigma }_n^2{\Sigma }_p\Phi ({\sigma }_n^{2}I+K{)}^{-1}\dots \dots (25)$$
将(25)式代入(23)的均值部分可得，
$$E[f_{\ast }]={\Phi }_{\ast }^T{\Sigma }_p\Phi ({\sigma }_n^{2}I+K{)}^{-1}Y$$
利用矩阵求逆引理(6)可得$A^{-1}$并带入(23)的协方差部分，可得
$$Cov[f_{\ast }]={\Phi }_{\ast }^T{\Sigma }_p{\Phi }_{\ast }-{\Phi }_{\ast }^T{\Sigma }_p\Phi ({\sigma }_n^{2}I+K{)}^{-1}{\Phi }^T{\Sigma }_p{\Phi }_{\ast }$$
最后，我们引入核函数这个概念，设核函数$K(X,X)={\Phi }^T{\Sigma }_p\Phi$,
以此类推，$K(X_{\ast },X)={\Phi }_{\ast }^T{\Sigma }_p\Phi$，$K(X_{\ast },X_{\ast })={\Phi }_{\ast }^T{\Sigma }_p{\Phi }_{\ast }$

我们这里介绍常用的高斯核函数$k(x,x^{\prime })={\sigma }^{2}exp\{\frac{|x-x^{\prime }{|}^2}{l}\}$，其中$l$是高斯过程的length-scale，这里不做过多解释。

最后的形式为
$$E[f_{\ast }]=K(X_{\ast },X)({\sigma }_n^{2}I+K(X,X){)}^{-1}Y$$
$$Cov[f_{\ast }]=K(X_{\ast },X_{\ast })-K(X_{\ast },X)({\sigma }_n^{2}I+K(X,X){)}^{-1}K(X,X_{\ast })$$
至此，权空间视角的推导过程就结束了。

下面是python实现代码：

gaussian_process_regression.py

import numpy as np


class GaussianProcessRegressor:
    """
    kernel: RBF(sigma_overall, l_scale)
    alpha: noise, 1-D array or scaler
    """
    def __init__(self, kernel, sigma_overall, l_scale, alpha=0.):
        self.kernel = kernel(sigma_overall, l_scale)
        self.alpha = alpha

    def fit(self, X, y):
        X = np.asarray(X)
        y = np.asarray(y)
        self.train_x_ = X
        self.train_y_ = y

    def predict(self, X, return_cov=True, return_std=False):
        if return_cov and return_std:
            raise RuntimeError("return_cov, return_std can't be True in the same time")
        if not hasattr(self, 'train_x_'):
            y_mean = np.zeros(X.shape[0])
            if return_cov:
                y_cov = self.kernel(X, X)
                return y_mean, y_cov
            elif return_std:
                y_cov = self.kernel(X, X)
                return y_mean, np.sqrt(np.diag(y_cov))
            else:
                return y_mean
        K = self.kernel(self.train_x_, self.train_x_)
        L = np.linalg.cholesky(K + self.alpha * np.eye(self.train_x_.shape[0]))
        alpha = np.linalg.solve(L, self.train_y_)
        alpha = np.linalg.solve(L.T, alpha)
        y_mean = self.kernel(self.train_x_, X).T @ alpha
        v = np.linalg.solve(L, self.kernel(self.train_x_, X))
        y_cov = self.kernel(X, X) - v.T @ v + self.alpha * np.eye(X.shape[0])
        if return_cov:
            return y_mean, y_cov
        elif return_std:
            return y_mean, np.sqrt(np.diag(y_cov))
        else:
            return y_mean

    def sample_func(self, X, n_samples=1):
        y_mean, y_cov = self.predict(X, return_cov=True, return_std=False)
        sampled_y = np.random.multivariate_normal(y_mean, y_cov, size=n_samples)
        return sampled_y

kernel.py

import numpy as np


class RBFKernel:
    def __init__(self, sigma, scale):
        self.sigma = sigma
        self.scale = scale

    def __call__(self, x1: np.ndarray, x2: np.ndarray):
        m, n = x1.shape[0], x2.shape[0]
        K_matrix = np.zeros((m, n), dtype=float)
        for i in range(m):
            for j in range(n):
                K_matrix[i, j] = self.sigma * np.exp(-0.5 * np.sum((x1[i] - x2[j]) ** 2) / self.scale)
        return K_matrix

测试代码：

from gaussian_process import RBFKernel, GaussianProcessRegressor
import numpy as np
import matplotlib.pyplot as plt


def get_y(x, alpha):
    return np.cos(x)*0.3 + np.random.normal(0, alpha, size=x.shape)

observation_size = 6
gpr = GaussianProcessRegressor(RBFKernel, sigma_overall=0.04, l_scale=0.5, alpha=1e-4)
sample_size = 3

test_x = np.linspace(0, 10, 100)
prior_mean, prior_cov = gpr.predict(test_x, return_cov=True)
sample_ys = gpr.sample_func(test_x, n_samples=sample_size)
uncertainty = 1.96 * np.sqrt(np.diag(prior_cov))

plt.plot(test_x, prior_mean, label='mean')
plt.fill_between(test_x, prior_mean-uncertainty, prior_mean+uncertainty, alpha=0.1)
for i in range(sample_size):
    plt.plot(test_x, sample_ys[i], linestyle='--')
plt.legend()
plt.title('prior')
plt.show()  # 至此绘制先验分布

train_x = np.array([3, 1, 4, 5, 7, 9])
train_y = get_y(train_x, alpha=1e-4)

gpr.fit(train_x, train_y)
y_mean, y_cov = gpr.predict(test_x, return_cov=True)
sample_ys = gpr.sample_func(test_x, n_samples=sample_size)
uncertainty = 1.96 * np.sqrt(np.diag(y_cov))

plt.plot(test_x, y_mean, label='mean', linewidth=3)
plt.fill_between(test_x, y_mean-uncertainty, y_mean+uncertainty, alpha=0.1)
for i in range(sample_size):
    plt.plot(test_x, sample_ys[i], linestyle='--')
plt.scatter(train_x, train_y, c='red', marker='x', label='observation', linewidths=5)
plt.legend()
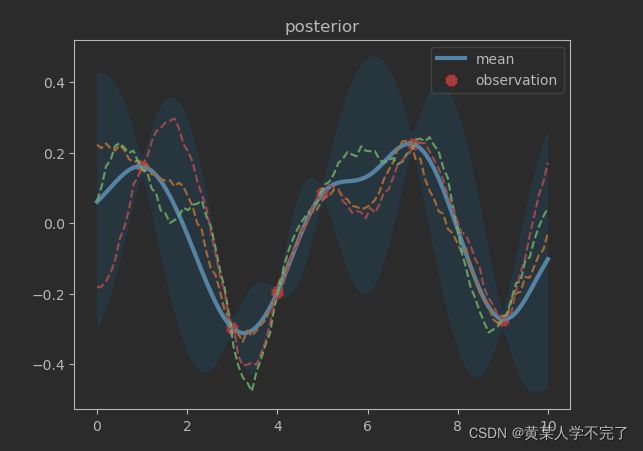
plt.title('posterior')
plt.show()  # 绘制后验分布

运行效果如下

下次补充函数空间的观点。

本人大二，水平有限，若有不严谨之处，请见谅。

参考文献

[1]C. E. Rasmussen & C. K. I. Williams.(2006). Gaussian Processes for Machine Learning.7-29.

[2]Christopher M. Bishop.(2007). Pattern Recognition and Machine Learning. 78-93.