MATLAB运用——计算船舶浮心(切面法)
在上一次的运用中,我们计算了水花号的质心。
在这一篇文章中,我们的任务是计算在任意水线下,浪花号的浮心。
问题:
计算浪花号在任意水线下的浮心。
分析
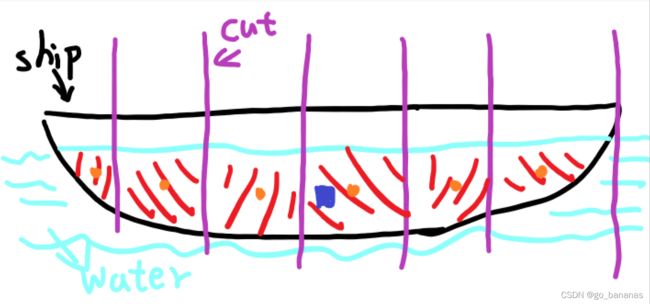
- 我们把船切成一个一个平面(紫色的线)
- 把【平面的面积X区间长度】近似地看作一个区间的排开水的体积(红色区域)
- 把每个区域的的水的质心算出来(橙色的点)
- 最后算出整体的质心就是船的浮心了(蓝色的点)
解决过程(完整代码在最后):
构建船体曲线
这次构造船体曲线和以往有些不同:
我们需要使用多项式拟合:原因是我们需要得到拟合图像的确切的公式。
有了这个公式我们才能计算出截面图形(定X变换Y得到Z)
同以前一样:我们把数据导入:

选择多项式拟合(我选择的是x,y各3次方):

我们就可以得到图像:
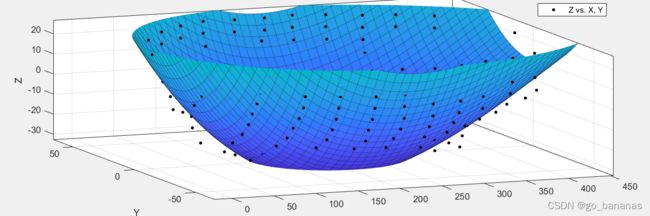
最关键的是得到拟合的公式:
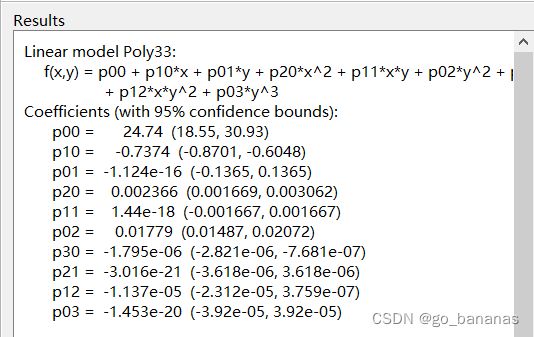
我们把这个公式写入matlab里面:我们就可以由x,y得到z了。
function z=caculate(x,y)
p00 = 24.74;
p10 = -0.7374;
p01 = -1.124e-16;
p20 = 0.002366;
p11 = 1.44e-18;
p02 = 0.01779;
p30 = -1.795e-06;
p21 = -3.016e-21;
p12 = -1.137e-05;
p03 = -1.453e-20;
z = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3 + p21*x^2*y
+ p12*x*y^2 + p03*y^3;
end
定义各项数据:(所有代码都是MATLAB下运行)
船体与水的相关:
clear all
boat.L = 400; %船的长度
boat.W = 100; %船的宽度
boat.HB = boat.W / 2; %船的半宽
boat.D = 60; %船的深度
boat.HD = boat.D / 2; %船的半宽
max_area = boat.D * boat.W %沿X轴的切面(Y_Z平面切面)的最大面积
max_volume = max_area * boat.L %立方体的体积
density_water = 28.312; %水的密度 (千克/立方英尺)
max_mass = max_volume * density_water %排开水的最大质量
微元相关
dy = 1; % meters(微元_Y轴)
dz = 1; % meters(微元_X轴)
mesh.ys = -boat.HB:dy:boat.HB; % meters Y轴切片
mesh.zs = -boat.HD:dz:boat.HD; % meters Z轴切片
[mesh.ygrid,mesh.zgrid] = meshgrid(mesh.ys,mesh.zs);
total_area = boat.W * boat.D %平方英尺
mesh.dA = total_area / numel(mesh.ygrid) %微元面积
浮心相关:
%XMass,YMass,ZMass记录的是每个切片的浮心(2D)
ZMass=[];
XMass=[];
YMass=[];
MMass=[];%每个浮心点的权重(质量)
tot_mass=0;%总质量
切片
%对每个x所对应的点切片:
for i=2 : 11 %对每个x积分
ZZ=[];%记录该X下的Z轴坐标
for j=1 : 101 %讨论y从[-60,60]
t=caculate(i*36,mesh.ys(1,j));
ZZ=[ZZ t];
end
y = mesh.ys;
figure(i);%绘制不同的图
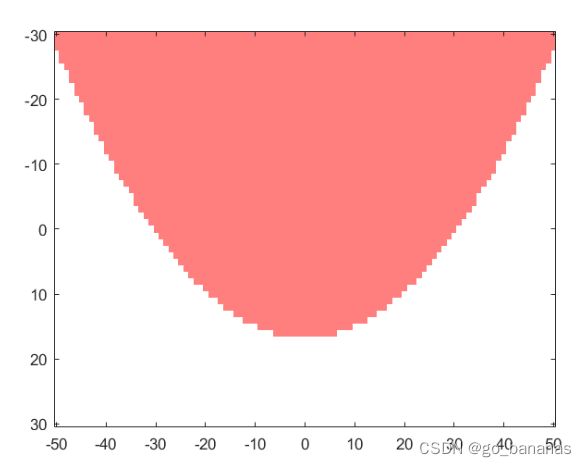
hull = mesh.zgrid > ZZ%在所计算的Z的值之上的就是船的截面
redmap = [1,1,1;1,0,0];
colormap(redmap);
image(mesh.ys,mesh.zs,flipud(hull),'AlphaData',0.5);
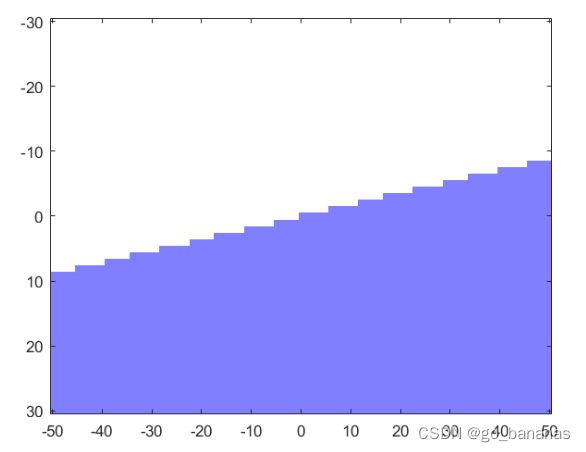
描述水线
%描述水线 y=kx+d
d = 0.05;
theta = 10;
y = mesh.ys;
z = tand(theta) .* y + d;%每个水线对应的方程
water = mesh.zgrid < z;
bluemap = [1,1,1; 0,0,1];
plotMatrix(water,mesh,bluemap);%画出水线
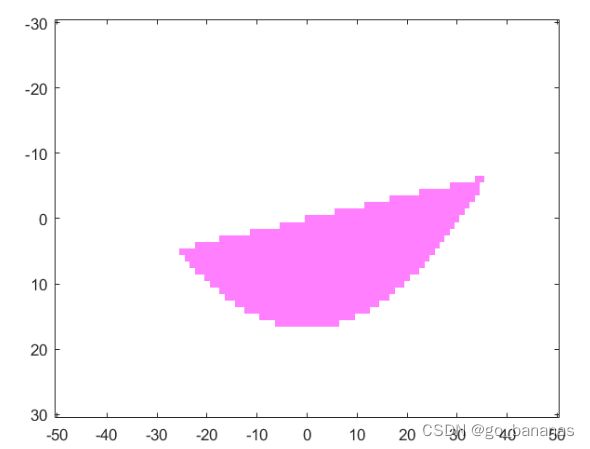
计算水线和船体的公共面积
%计算水线与切面的公共面积
sub_region = hull & water;%&位与运算(都是1才得1)
purplemap = [1,1,1; 1,0,1];
plotMatrix(sub_region,mesh,purplemap);%绘制图像
分别计算每个区域的质心(2D)
%计算浮心2D
COB = centerOfMass2(sub_region,mesh);
function M = matrixSum(A)
% matrixSum: returns total of all elements in the matrix
% A: matrix
% returns: scalar
% normally sum(m) computes the sums of the columns
% selecting m(:) flattens the matrix and computes the sum of all elements
% see https://stackoverflow.com/questions/1721987/what-are-the-ways-to-sum-matrix-elements-in-matlab
M = sum(A(:));
end
function COM = centerOfMass2(masses,mesh)
% centerOfMass2: computes center of mass in 2D
% masses: matrix of masses
% mesh: structure containing ygrid and zgrid
% returns: Vector [ycom,zcom]
M = matrixSum(masses);
ycom = matrixSum(masses .* mesh.ygrid) / M;
zcom = matrixSum(masses .* mesh.zgrid) / M;
COM = [ycom,zcom];
end
再根据2D的质心计算浮心(3D)
ANS=centerOfMass3(XMass,YMass,ZMass,MMass,tot_mass);%计算三维浮心
function ANS=centerOfMass3(XMass,YMass,ZMass,MMass,m)
x=0;
y=0;
z=0;
for i=1:10
x=x+XMass(1,i)*MMass(1,i)/m;
y=y+YMass(1,i)*MMass(1,i)/m;
z=z+YMass(1,i)*MMass(1,i)/m;
end
ANS=[x,y,z];
end
最后得到浪花号在z=tan(10)y+0.05的水线下的浮心是:
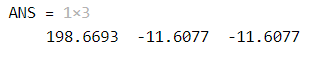
完整代码:(.mlx)
这是用多项式拟合出来的函数图像数据
X = [ 0.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 432.000000 ];
Y = [ 0.000000 -27.750000 -27.750000 -17.000000 -16.000000 -9.750000 -7.500000 7.500000 9.750000 16.000000 17.000000 27.750000 27.750000 -41.750000 -41.750000 -39.375000 -36.500000 -32.500000 -29.500000 -24.375000 -16.500000 -9.750000 9.750000 16.500000 24.375000 29.500000 32.500000 36.500000 39.375000 41.750000 41.750000 -51.250000 -50.875000 -50.875000 -49.750000 -46.250000 -41.250000 -36.250000 -27.500000 -16.250000 -6.250000 6.250000 16.250000 27.500000 36.250000 41.250000 46.250000 49.750000 50.875000 50.875000 51.250000 -57.250000 -57.250000 -55.250000 -54.000000 -51.875000 -48.625000 -44.125000 -35.250000 -25.500000 -9.250000 9.250000 25.500000 35.250000 44.125000 48.625000 51.875000 54.000000 55.250000 57.250000 57.250000 -59.750000 -58.750000 -56.750000 -56.250000 -56.250000 -53.500000 -51.125000 -41.750000 -27.500000 -14.750000 14.750000 27.500000 41.750000 51.125000 53.500000 56.250000 56.250000 56.750000 58.750000 59.750000 -58.750000 -58.250000 -58.000000 -56.500000 -56.500000 -55.250000 -49.250000 -43.000000 -28.750000 -17.500000 17.500000 28.750000 43.000000 49.250000 55.250000 56.500000 56.500000 58.000000 58.250000 58.750000 -58.500000 -58.500000 -57.250000 -57.000000 -56.750000 -53.875000 -50.000000 -46.500000 -16.250000 -15.250000 15.250000 16.250000 46.500000 50.000000 53.875000 56.750000 57.000000 57.250000 58.500000 58.500000 -55.750000 -55.750000 -55.000000 -54.750000 -53.500000 -49.000000 -43.500000 -33.000000 -19.500000 -10.750000 10.750000 19.500000 33.000000 43.500000 49.000000 53.500000 54.750000 55.000000 55.750000 55.750000 -50.500000 -50.500000 -50.000000 -48.500000 -48.000000 -45.500000 -33.500000 -21.000000 -11.500000 -8.750000 8.750000 11.500000 21.000000 33.500000 45.500000 48.000000 48.500000 50.000000 50.500000 50.500000 -48.000000 -48.000000 -47.500000 -45.875000 -43.000000 -34.000000 -16.875000 -10.500000 -6.500000 -4.500000 4.500000 6.500000 10.500000 16.875000 34.000000 43.000000 45.875000 47.500000 48.000000 48.000000 -42.625000 -41.375000 -41.000000 -41.000000 -33.500000 -11.500000 11.500000 33.500000 41.000000 41.000000 41.375000 42.625000 0.000000 ];
Z = [ 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 12.000000 18.000000 24.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 18.000000 24.000000 12.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 12.000000 6.000000 0.000000 24.000000 18.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 18.000000 24.000000 0.000000 6.000000 12.000000 12.000000 6.000000 0.000000 24.000000 18.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 18.000000 24.000000 0.000000 6.000000 12.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 6.000000 12.000000 24.000000 18.000000 0.000000 -6.000000 -6.000000 0.000000 24.000000 18.000000 12.000000 6.000000 24.000000 ];
[a,b]=createFit(X,Y,Z)
axis('equal');%使得各个坐标轴长度相等
zlim([-40,40]);%限定Z轴范围[-40,40]
计算浮心(单位:英尺):
clear all
boat.L = 400; %船的长度
boat.W = 100; %船的宽度
boat.HB = boat.W / 2; %船的半宽
boat.D = 60; %船的深度
boat.HD = boat.D / 2; %船的半宽
max_area = boat.D * boat.W %沿X轴的切面(Y_Z平面切面)的最大面积
max_volume = max_area * boat.L %立方体的体积
density_water = 28.312; %水的密度 (千克/立方英尺)
max_mass = max_volume * density_water %排开水的最大质量
从Y,Z轴切片(取微元):
dy = 1; % meters(微元_Y轴)
dz = 1; % meters(微元_X轴)
mesh.ys = -boat.HB:dy:boat.HB; % meters Y轴切片
mesh.zs = -boat.HD:dz:boat.HD; % meters Z轴切片
[mesh.ygrid,mesh.zgrid] = meshgrid(mesh.ys,mesh.zs);
total_area = boat.W * boat.D %平方英尺
mesh.dA = total_area / numel(mesh.ygrid) %微元面积
XMass,YMass,ZMass记录的是每个切片的浮心(2D)
ZMass=[];
XMass=[];
YMass=[];
MMass=[];%每个浮心点的权重(质量)
tot_mass=0;%总质量
对每个x所对应的点切片:
for i=2 : 11 %对每个x积分
ZZ=[];%记录该X下的Z轴坐标
for j=1 : 101 %讨论y从[-60,60]
t=caculate(i*36,mesh.ys(1,j));
ZZ=[ZZ t];
end
y = mesh.ys;
figure(i);%绘制不同的图
hull = mesh.zgrid > ZZ%在所计算的Z的值之上的就是船的截面
redmap = [1,1,1;1,0,0];
colormap(redmap);
image(mesh.ys,mesh.zs,flipud(hull),'AlphaData',0.5);
%描述水线 y=kx+d
d = 0.05;
theta = 10;
y = mesh.ys;
z = tand(theta) .* y + d;%每个水线对应的方程
water = mesh.zgrid < z;
bluemap = [1,1,1; 0,0,1];
plotMatrix(water,mesh,bluemap);
%计算水线与切面的公共面积
sub_region = hull & water;%&位与运算(都是1才得1)
purplemap = [1,1,1; 1,0,1];
plotMatrix(sub_region,mesh,purplemap);%绘制图像
%计算浮心2D
COB = centerOfMass2(sub_region,mesh);
ZMass=[ZMass COB(1,1)];
YMass=[YMass COB(1,2)];
XMass=[XMass (i-0.5)*36];
MMass=[MMass matrixSum(sub_region)];
tot_mass=tot_mass+matrixSum(sub_region);
end
ANS=centerOfMass3(XMass,YMass,ZMass,MMass,tot_mass);%计算三维浮心
ANS
function ANS=centerOfMass3(XMass,YMass,ZMass,MMass,m)
x=0;
y=0;
z=0;
for i=1:10
x=x+XMass(1,i)*MMass(1,i)/m;
y=y+YMass(1,i)*MMass(1,i)/m;
z=z+YMass(1,i)*MMass(1,i)/m;
end
ANS=[x,y,z];
end
function M = matrixSum(A)
% matrixSum: returns total of all elements in the matrix
% A: matrix
% returns: scalar
% normally sum(m) computes the sums of the columns
% selecting m(:) flattens the matrix and computes the sum of all elements
% see https://stackoverflow.com/questions/1721987/what-are-the-ways-to-sum-matrix-elements-in-matlab
M = sum(A(:));
end
function COM = centerOfMass2(masses,mesh)
% centerOfMass2: computes center of mass in 2D
% masses: matrix of masses
% mesh: structure containing ygrid and zgrid
% returns: Vector [ycom,zcom]
M = matrixSum(masses);
ycom = matrixSum(masses .* mesh.ygrid) / M;
zcom = matrixSum(masses .* mesh.zgrid) / M;
COM = [ycom,zcom];
end
function plotMatrix(A,mesh,cmap)
% plotMatrix: plots a matrix using image
% A: matrix
% mesh: srtruct containing ys and zs
% cmap: Colormap
colormap(cmap);
image(mesh.ys,mesh.zs,flipud(A),'AlphaData',0.5);
end
function [fitresult, gof] = createFit(X, Y, Z)
%CREATEFIT(X,Y,Z)
% Create a fit.
%
% Data for 'untitled fit 1' fit:
% X Input : X
% Y Input : Y
% Z Output: Z
% Output:
% fitresult : a fit object representing the fit.
% gof : structure with goodness-of fit info.
%
% 另请参阅 FIT, CFIT, SFIT.
% 由 MATLAB 于 12-Mar-2022 16:36:02 自动生成
%% Fit: 'untitled fit 1'.
[xData, yData, zData] = prepareSurfaceData( X, Y, Z );
% Set up fittype and options.
ft = fittype( 'poly33' );
% Fit model to data.
[fitresult, gof] = fit( [xData, yData], zData, ft, 'Normalize', 'on' );
% Plot fit with data.
figure( 'Name', 'untitled fit 1' );
h = plot( fitresult, [xData, yData], zData );
legend( h, 'untitled fit 1', 'Z vs. X, Y', 'Location', 'NorthEast', 'Interpreter', 'none' );
% Label axes
xlabel( 'X', 'Interpreter', 'none' );
ylabel( 'Y', 'Interpreter', 'none' );
zlabel( 'Z', 'Interpreter', 'none' );
grid on
view( 10.1, 31.6 );
end
多项式函数拟合部分:
Linear model Poly33:
f(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3 + p21*x^2*y
+ p12*x*y^2 + p03*y^3
Coefficients (with 95% confidence bounds):
p00 = 24.74 (18.55, 30.93)
p10 = -0.7374 (-0.8701, -0.6048)
p01 = -1.124e-16 (-0.1365, 0.1365)
p20 = 0.002366 (0.001669, 0.003062)
p11 = 1.44e-18 (-0.001667, 0.001667)
p02 = 0.01779 (0.01487, 0.02072)
p30 = -1.795e-06 (-2.821e-06, -7.681e-07)
p21 = -3.016e-21 (-3.618e-06, 3.618e-06)
p12 = -1.137e-05 (-2.312e-05, 3.759e-07)
p03 = -1.453e-20 (-3.92e-05, 3.92e-05)
function z=caculate(x,y)
p00 = 24.74;
p10 = -0.7374;
p01 = -1.124e-16;
p20 = 0.002366;
p11 = 1.44e-18;
p02 = 0.01779;
p30 = -1.795e-06;
p21 = -3.016e-21;
p12 = -1.137e-05;
p03 = -1.453e-20;
z = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3 + p21*x^2*y
+ p12*x*y^2 + p03*y^3;
end
可待提升的空间:
- 多项式拟合可以使用更高的次数,结果会更精确。
- 船的切片可以切得更密集一些,这样进度会更高。下面是制造更多切面的代码(C++)
#include