Swin-Unet：Swin Transformer在医学分割上的首次尝试

Swin-Unet：Swin Transformer在医学分割上的首次尝试

前言

最近小编主要在搞一些医学图像分割的工作，也跑了一下Swin-Unet,之前看到也看到过这篇Swin-Unet(其实五月份就看到了hhhh)，决定搬运过来。实际上从这篇论文可以看到目前医学分割或者检测引入transformer，更常见的做法还是直接嵌入到医学图像常用的网络结构中，比如Unet系列等，没有对transformer block做更多的创新，这主要是由于医学图像数据集太小导致对于transformer本身进行创新难以通过医学图像数据集进行实验验证。后续小编将持续更新医学图像分割相关的论文解读系列~~本篇文章应该是今年5月份左右挂到Arxiv上的，工作的创新主要基于今年3月微软的Swin Transformer工作(ps:Swin Transformer刚刚获得ICCV2021最佳论文奖，所以Swin-Unet真的是站在了巨人的肩膀上，hhhhhhh)

一、Related Works

作者首先对最近医学分割领域的相关工作进行了总结，主要有以下三种：

1. CNN-based methods
   以Unet为backbone的一系列变种，比如Unet++,Unet3+,Att-Unet

2. Transformer-based methods
   ViT/DeiT,DerT

3. CNN+Transformer
   两者结合的理由也非常好理解，CNN注重local dependency提取，transformer注重global和long-range dependency提取。举个例子：TransUnet中证明了hybrid encoder优于CNN-based and transformer-based

二、Architecture Overview

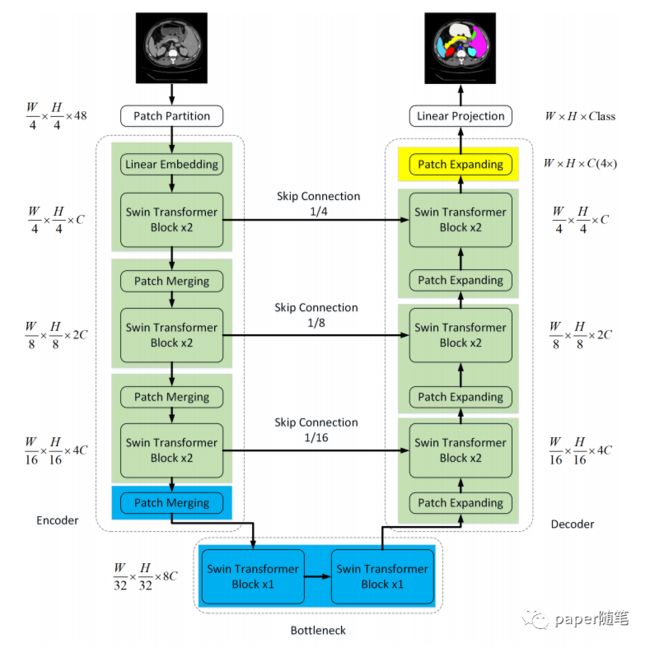
整个网络框架如下图所示，可以发现整体就是一个Unet结构，只不过encoder和decoder部分换成了Swin Transformer block，细节部分我们将分为以下几点具体讲解：

• Swin Transformer
• Patch Merging && Patch Expanding
• Comparison with Unet
  

Swin Transformer

第一部分先介绍一下Swin Transformer,先上Swin transformer block的结构图看一波~

典型的transformer encoder的结构，主要关注点应该是W-MSA(window based MSA)和SW-MSA(shifted window based MSA)，这两个组件也是Swin Transformer论文的创新点，下面通过以下计算复杂度的介绍来回顾下作者提出用这个东西来代替单纯的MSA的初衷：

一个MSA的计算复杂度为：

我们首先看一下如何得到当前的公式，对于一张图像，我们将其分为$h\times w$个patch，同时设每个patch经过embedding之后的feature dimension为$C$，其中$C$一般为$d_{model}$,$d$为heads的数量。

一起来回顾下MSA的计算:

第一步：计算Q，K，V矩阵，计算量为$3hw{C}^2/d$
$$Q=X{W}^Q$$$$K=X{W}^K$$$$V=X{W}^V$$
(以Q的计算为例，其中X维度为$hw\times C$, $W^Q$维度为$C\times C/d$ , 以此类推）

第二步：计算$Q{K}^{T}V$,计算量为$2(hw{)}^{2}C/d$
(其中$Q{K}^T$的计算量为$(hw{)}^{2}C/d$

第三步：一个head的计算量为$3hw{C}^2/d+2(hw{)}^{2}C/d$,那么d个head的计算量为$3hw{C}^2+2(hw{)}^{2}C$

第四步：最后将d个head进行融合，和矩阵$W^o$相乘，计算量为$hw{C}^2$,因此总计算量为$4hw{C}^2+2(hw{)}^{2}C$

可以看到MSA的计算复杂度是$O({n_p}^2)$,其中$n_p$为patch的数量，很显然计算量太大，对于大尺度的图片很不友好，显存占用会比较夸张。那么我们来看下一个W-MSA的计算复杂度（顾名思义就是把图像分为几个window,一个window中假设有$M\times M$个patch,那么我们只对这个window中所有patch计算attention,提取局部的依赖关系），W-MSA的计算复杂度为：

所以比较好理解，对于一个window来说，计算量只需要把$4hw{C}^2+2(hw{)}^{2}C$中的$h$,$w$分别替换为$M$，那么一个window的计算量为$4M^2{C}^2+2M^{4}C$,共有$\frac{hw}{M^2}$个window，就可以得到上述式子。

如果仔细阅读的话可以发现，这样做实际上是有问题的，没错，各个window和window内的patch之间就没有interaction了，为了解决这个问题，我们非常容易想到shifted window，即让window移动一下不就可以了吗，如下图：

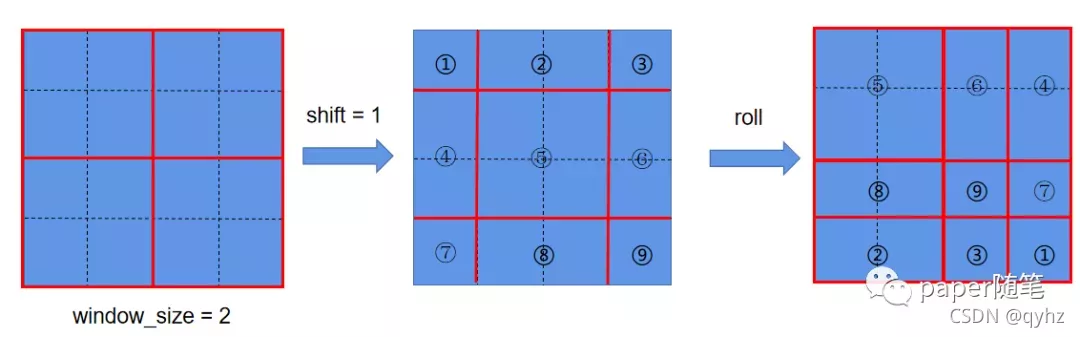
如上图中，可以发现在经过shift=$\frac{1}{2}$window_size之后出现了window_size大小不一致的问题，如果只简单的添加padding，计算量还是增加了，(因为窗口数量由$2\times 2$变成 $3\times 3$)。因此作者又进行了一个cycle shift操作，这样操作完之后继续按照之前的窗口大小进行划分，并对每一个窗口的patch进行self-attention进行计算。以现在的第一个window(index=5)为例，包含的这四个patch分别来自于shift之前的四个窗口，而每个patch又和之前窗口中的patch进行过交互，所以再次计算第一个window中的patch之间的attention就相当于完成了window间的交互。然而，这样计算还是会存在一些问题，（比如左上角窗口中所有的patch的index都是5，但是右下角的窗口中包含了来自index分别为1，3，7，9的四个patch, 而这些位置并不相邻，计算意义不大）因此作者引入了attention mask(以最后一个window为例）：

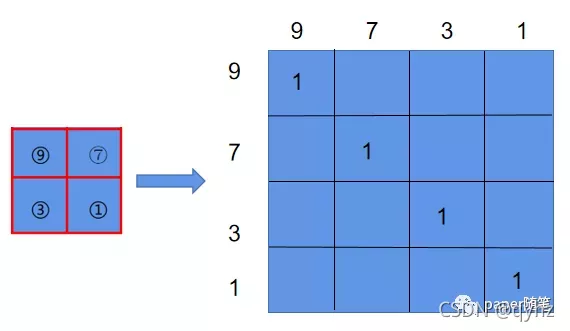
添加类似于上图的mask之后就可以避免不同的index的patch之间进行计算。
代码如下（示例）：

H, W = self.input_resolution
            img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1
            h_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))
            w_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))
            cnt = 0
            for h in h_slices:
                for w in w_slices:
                    img_mask[:, h, w, :] = cnt
                    cnt += 1

            mask_windows = window_partition(img_mask, self.window_size)  # nW, window_size, window_size, 1
            mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
            attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
            attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

简单理解来说，就是生成一张attention mask，每个位置的值为0或者-100，取决于index是否相同，再与我们计算出来的$Q{K}^T$矩阵相加，这样index不同位置的attention值就降到了很低，那么softmax值就会比较低。
事实上，在window partition过程中，当整个feature map不能被完全整分为windows时，此时我们除了增加padding之外，也可以尝试这种方法生成attention mask，这样做更加准确而且不改变feature map的大小。

以上就是swin transformer具体的一个block的讲解。

Patch Merging

在Swin Transformer的论文中作者已经提出了Patch Merging的概念，我们先看下Swin-Transformer的整体结构：

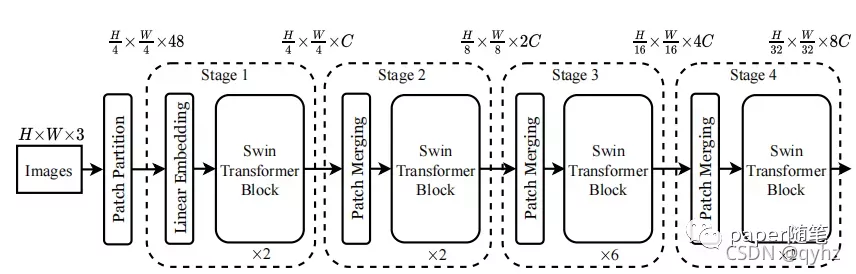
从stage中出现Patch Merging，Patch Merging中进行的操作是：

首先进行 ，具体操作通过将每个patch周围的patch的feature进行concat，此时dimension为输入的4倍，通过一个linear projection将其转为输入的2倍。
代码如下（示例）：

class PatchMerging(nn.Module):
    r""" Patch Merging Layer.

    Args:
        input_resolution (tuple[int]): Resolution of input feature.
        dim (int): Number of input channels.
        norm_layer (nn.Module, optional): Normalization layer.  Default: nn.LayerNorm
    """

    def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
        super().__init__()
        self.input_resolution = input_resolution
        self.dim = dim
        self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
        self.norm = norm_layer(4 * dim)

    def forward(self, x):
        """
        x: B, H*W, C
        """
        H, W = self.input_resolution
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"
        assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."

        x = x.view(B, H, W, C)

        x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
        x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
        x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
        x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
        x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
        x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C

        x = self.norm(x)
        x = self.reduction(x)

        return x

上述的Patch Merging和Patch Expanding做法类似pixel unshuffle/shuffle操作。

Relative Position Embedding

在论文中作者提到了在原本计算attention的基础上添加相对位置的编码，如下公式所示：

至于为什么引入相对位置编码代替绝对位置编码，可以分别从理论+实验上进行证明，简单来说，在计算过程中，相对位置信息会“消失”，这是ViT在提出时没有注意到的问题，作者也做了实验，证明本文提出的relative position 优于ViT中absolute position以及rel+abs组合的方法：

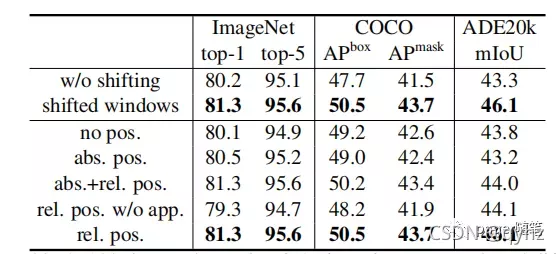
相对位置编码索引计算过程如下：

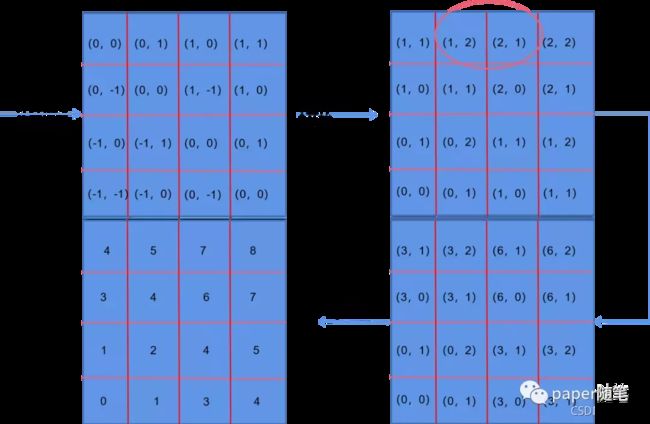
代码如下（示例）：

self.relative_position_bias_table = nn.Parameter(
            torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads))  # 2*Wh-1 * 2*Ww-1, nH

# get pair-wise relative position index for each token inside the window
coords_h = torch.arange(self.window_size[0])
coords_w = torch.arange(self.window_size[1])
coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1  # shift to start from 0
relative_coords[:, :, 1] += self.window_size[1] - 1
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww
self.register_buffer("relative_position_index", relative_position_index)

这里链接中的博主讲的比较清楚，每一步都有具体的讲解。(大概过程是生成了一张可以索引的relative position table）
https://zhuanlan.zhihu.com/p/384514268

Patch Expanding

与merging操作相反，首先经过linear projection将维度拓展2倍，接着进行rearrange operation（操作即为merging的逆过程），为了证明此种方法有效，作者和传统的上采样方法进行了比较：

代码如下（示例）：

class PatchExpand(nn.Module):
    def __init__(self, input_resolution, dim, dim_scale=2, norm_layer=nn.LayerNorm):
        super().__init__()
        self.input_resolution = input_resolution
        self.dim = dim
        self.expand = nn.Linear(dim, 2*dim, bias=False) if dim_scale==2 else nn.Identity()
        self.norm = norm_layer(dim // dim_scale)

    def forward(self, x):
        """
        x: B, H*W, C
        """
        H, W = self.input_resolution
        x = self.expand(x)
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"

        x = x.view(B, H, W, C)
        x = rearrange(x, 'b h w (p1 p2 c)-> b (h p1) (w p2) c', p1=2, p2=2, c=C//4)
        x = x.view(B,-1,C//4)
        x= self.norm(x)

        return x

Comparison with Unet

很显然，整篇论文的思路就是把UNet中CNN换成swin-transformer结构，左边为下采样+通道扩张，右边为上采样+通道压缩。

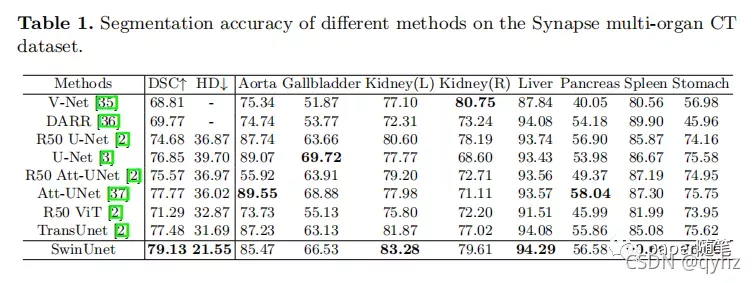
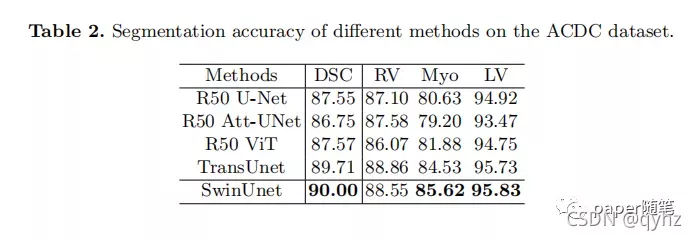
三、Experiments

四、Views on related works about transformer（七月份写的）

最近大概读了些最新的transformer的论文，主要是关于医学分割方向的，简单地在此谈谈下一步可创新的点：

1.引入MLP

目前三篇论文《Do you even need attention》，《external attention》，《remlp》都在暗示self-attention是否可以直接被MLP取代，《Do you even need attention》中发现将ViT中的self-attention替换为patch dimension的MLP效果也非常好，同时也做了将feature dimension的FFN替换为self-attention但是效果就很差，作者认为viT之所以表现不错的原因可能取决于patch embedding以及训练过程；《external attention》中认为计算self-attention时 的计算没有必要，因为一个位置的特征只与周围近距离的几个点的值有关，同时为了挖掘样本之间的关系，将self-attention长距离建模拓展到样本的层面上，提出了使用两个外部的记忆单元（代码中用了两个全连接层），事实上，对这两个全连接层能否很好地像self-attention一样对单个样本中patch之间进行建模不能确定，或者说是否和self-attention相结合效果会更好？

2.结合医学图像特点，做的更细致

虽然引入了transformer，但可以看出，也仅仅是使用了，还没有很好地结合医学图像做更多地细化工作，后续双transformer,多尺度的transformer融合分割等可以搞起来了…最近也在看些半监督的论文，加入半监督的transformer说不定也可以发起来。

plus:前些天也读了一篇《CAT:Cross attention in vision transformer》，和swin-transformer有点异曲同工的感觉，分成了IPSA和CPSA，主要也是考虑到了transformer忽略了单个patch中的结构相关性以及最重要的可能是模仿mobile net（作者也提到了）减少计算量，实验结果和swin-T相比不相上下。

3.CNN的那一套改进的可以在transformer上再过一遍了

刚看到可变形的transformer出来了…

后续小编将继续进行更新~~~~~~~~~~~~~~~~~~~~~~~~~