从线性回归到高斯过程回归

1.数据集

假设我们有这样一个数据集：$$\mathcal{D}=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$$其中每个$x_i$为一个$p$维列向量，每个$y_i$是一个标量。
我们将该数据集用矩阵的形式表示：$$X_{N\times p}=\left[\begin{array}{c}{x}_1^T\\ x_2^T\\ \cdots \\ x_N^T\end{array}\right],Y_{N\times 1}=\left[\begin{array}{c}{y}_1\\ y_2\\ \cdots \\ y_N\end{array}\right]$$则线性回归假设可以表示为$f(w)=w^{T}x$
其中$w$是一个$p$维列向量。
回归问题的终极目标就是求$w$的值(方法：频率派的最小二乘法和极大似然估计、贝叶斯派的极大后验估计)，或者生成关于$w$的概率分布(方法：贝叶斯派的贝叶斯估计)。

2.最小二乘法

2.1.解法

既然是频率派，我们惯用的套路就是先建立一个模型，将我们的训数据集中的$x_i$输入到模型中，输出就是我们预测的$\widehat{y_i}$，将预测值$\widehat{y_i}$与真实值$y_i$作比较，计算损失函数，通过最小化失函数来优化模型中的参数$w$，使得$w$可以尽量去拟合数据集真实的分布。
最小二乘法采用平方误差来定义损失函数公式$$\begin{array}{rl}& L(w)=\sum _{i=1}^N(w^T{x}_i-y_i{)}^2\\ & =[w^T{x}_1-y_1,w^T{x}_2-y_2,\cdots ,w^T{x}_N-y_N]\left[\begin{array}{c}{w}^T{x}_1-y_1\\ w^T{x}_2-y_2\\ \cdots \\ w^T{x}_N-y_N\end{array}\right]\\ & =[w^T{x}_1-y_1^T,w^T{x}_2-y_2^T,\cdots ,w^T{x}_N-y_N^T]\left[\begin{array}{c}{x}_1^{T}w-y_1\\ x_2^{T}w-y_2\\ \cdots \\ x_N^{T}w-y_N\end{array}\right]\\ & =(w^T{X}^T-Y^T)(Xw-Y)\\ & =w^T{X}^{T}Xw-Y^{T}Xw-w^T{X}^{T}Y+Y^{T}Y\\ & =w^T{X}^{T}Xw-2w^T{X}^{T}Y+Y^{T}Y\end{array}\text{\hspace{1em}(1)}$$$L(w)$是一个凸函数，最小化$L(w)$可以自然而然的想到将$L(w)$对$w$求导，令导函数为0：
$$\begin{array}{rl}& \frac{\partial L(w)}{\partial w}=0\\ & 2X^{T}Xw-2X^{T}Y=0\\ & w=(X^{T}X{)}^{-1}{X}^{T}Y=X^{†}Y\end{array}\text{\hspace{1em}(2)}$$
(2)中，$X^{†}=(X^{T}X{)}^{-1}{X}^T$又被称之为伪逆。显然若$X^{T}X$可逆，那么可以直接求解。否则，我们可以求$X$的奇异值分解$X=U\Sigma V^T$，其中$\Sigma$是一个满秩方阵。那么$$\begin{array}{rl}& X^{†}=(V{\Sigma }^T{U}^{T}U\Sigma V^T{)}^{-1}V{\Sigma }^T{U}^T\\ & =V({\Sigma }^T\Sigma {)}^{-1}{V}^{T}V\Sigma U^T\\ & =V({\Sigma }^T\Sigma {)}^{-1}\Sigma U^T\\ & =V{\Sigma }^{†}{U}^T\end{array}\text{\hspace{1em}(3)}$$

2.2.直观理解

求$w$的问题实际上就是求解方程$Xw=Y$。
为了表述方便，我们采取另一种形式表示$X$：
在$X$中，$x_i^T$就是一个$p$维的行向量，令$x_i^T=[x_i^1,x_i^2,\cdots ,x_i^p]$
那么数据集在第一个维度上可表示为：$x^1=\left[\begin{array}{c}{x}_1^1\\ x_2^1\\ \cdots \\ x_N^1\end{array}\right]$
那么$X$就可以表示为$X=[x^1,x^2,\cdots ,x^p]$
由线性代数的知识我们可以得到
假设我们的训练样本张成一个$p$维空间$\mathcal{X}$($X$列满秩)：$\mathcal{X}=Span(x_1,\cdots ,x_N)$
那么$Xw$就是$\mathcal{X}$的基向量$[x^1,x^2,\cdots ,x^p]$关于$w$的线性组合，其可以表示为$\mathcal{X}$中的向量$\hat{Y}$，$w$是$p$维基空间$\mathcal{I}$中的向量。当然，求解$w$就是希望$\hat{Y}$和$Y$越近越好。

若$X$是$p\times p$的方阵且满秩，那么$Y$是$p$维向量，可与通过空间逆变换将$\mathcal{X}$中的$Y$映射到基空间$\mathcal{I}$中得到$w$。PS:有关这一点可以参考b站3Blue1Brown的系列视频-线性代数的本质-03-矩阵与线性变换

若$N>p$且$X$列满秩，对于低维空间$\mathcal{X}$和高维向量$Y$，显然$Y$不在$\mathcal{X}$中，那么此时我们可以求$\mathcal{X}$中与$Y$最近的那个向量，是哪个呢？显然将$Y$往低维空间$\mathcal{X}$中投影得到的向量就是最近的那个，该向量在$\mathcal{X}$中的基向量的线性组合就是$w$。

若 N < p N

N<p且$X$行满秩，那么高维空间$N$中显然可以找到无数个$w$映射到低维空间可以与$Y$重合。

2.3.条件数

既然我们通过最小二乘法得到了$w$，那么我们自然就要研究其数值稳定性，也就是当$Y$发生扰动时，$w$的变化幅度。
不妨假设$A$为方阵且可逆，则对于$Ax=b$有$x=A^{-1}b$。
条件数定义为$$cond(A)=\frac{||\Delta x||\setminus ||x||}{||\Delta b||\setminus ||b||}=\frac{||\Delta x||\cdot ||b||}{||x||\cdot ||\Delta b||}=\frac{||A^{-1}\Delta b||\cdot ||Ax||}{||\Delta b||\cdot ||x||}\text{\hspace{1em}(4)}$$
已知$A$的范数可表示为$||A||=\underset{x\ne 0}{\max }\frac{||Ax||}{||x||}$
那么$$cond(A)\le ||A||\cdot ||A^{-1}||\text{\hspace{1em}(5)}$$当条件数$cond(A)$较小时，若初始条件发生较小的变化，解的变化不大，$A$就是良态矩阵；
当条件数$cond(A)$较大时，如初始条件发生较小的变化，解的变化很大，$A$就是病态矩阵。

2.4.QR分解

先说结论：利用对$X$作$QR$分解的方式求解可以保证数值的稳定性。
对矩阵$X$，若$N\ge p$,则$X$可被分解成X=QR ，其中$Q_{N\times N}$是正交矩阵($Q^{T}Q=Q{Q}^T=I$)，$R_{N\times p}=\left[\begin{array}{c}{\hat{R}}_{p\times p}\\ 0\end{array}\right]$，${\hat{R}}_{p\times p}$是上三角矩阵。$||Xw-Y|{|}_2^2$内部左乘一正交矩阵对结果不影响。因此，$$L(w)=||Xw-Y|{|}_2^2=||QRw-Y|{|}_2^2=||Q^{T}QRw-Q^{T}Y|{|}_2^2=||\left[\begin{array}{c}\hat{R}\\ 0\end{array}\right]w-Q^{T}Y|{|}_2^2\text{\hspace{1em}(6)}$$将$Q^{T}Y$拆成与$\left[\begin{array}{c}\hat{R}\\ 0\end{array}\right]$类似的上下两部分：$\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]$，$$L(w)=||\left[\begin{array}{c}\hat{R}w-c_1\\ -c_2\end{array}\right]|{|}_2^2=||\hat{R}w-c_1|{|}_2^2+||c_2|{|}_2^2\text{\hspace{1em}(7)}$$$||c_2|{|}_2^2$为常数，因此我们只能最小化(7)前一部分使得$||\hat{R}w-c_1|{|}_2^2=0$，则有$\hat{R}w-c_1=0$，那么$L(w)$的最小值为$||c_2|{|}_2^2$。这样处理之后就避免了求正规方程组中的$(X^{T}X{)}^{-1}$，避免条件数变成$cond(X^{T}X)=cond(X{)}^2$，保证了数值的稳定性。

3.噪声为高斯分布的 MLE

先说结论：最小二乘估计$\iff$噪声服从正态分布的极大似然估计
对于一维的情况，记$y=w^{T}x+ϵ,ϵ\sim \mathcal{N}(0,{\sigma }^2)$，
那么$y\sim \mathcal{N}(w^{T}x,{\sigma }^2)$，$p(y_i|x_i,w)=\frac{1}{\sqrt{2\pi }\sigma }exp\{-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\}$
代入极大似然估计中：
$$\begin{array}{rl}& L(w)=\log p(Y|X,w)\\ & =\log \prod _{i=1}^{N}p(y_i|x_i,w)\\ & =\sum _{i=1}^N\log (\frac{1}{\sqrt{2\pi }\sigma }exp\{-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\})\end{array}\text{\hspace{1em}(8)}$$$$\begin{array}{r}w=\underset{w}{\mathrm{argmax}}L(w)=\underset{w}{\mathrm{argmin}}\sum _{i=1}^N(y_i-w^T{x}_i{)}^2\end{array}\text{\hspace{1em}(9)}$$(9)和最小二乘估计得到的结果一样。

4. 过拟合

我们用多项式回归来说明其中的过拟合现象。
首先我们应该意识到，多项式回归$\iff$线性回归。
例如我们用下面形式的多项式函数来拟合函数：$$y(x,\text{w})=w_0+w_{1}x+w_2{x}^2+\cdots +w_p{x}^p=\sum _{i=0}^p{w}_i{x}^i$$可以看到，当$\text{w}=[w_1,w_2,\cdots ,x_p{]}^T,b=w_0,\text{x}=[x^1,x^2,x^3,\cdots ,x^p{]}^T$时，多项式回归相当于高维度线性回归在低维空间的表现形式。
再举一个更具体的例子：比如我们在二维空间拟合二次多项式曲线$y=x+x^2$，就相当于在三维空间拟合平面$z=x+y$，该曲线即为三维空间中$z=x+y,y=x^2$两个面的交线，二维空间中数据分布在曲线周围，三维空间中数据分布在交线周围，也在平面$z=x+y$上。因此低维空间的非线性问题在高维空间的线性问题。
而过拟合问题就是，由于数据量太少，维度太高，在二维空间把要拟合的直线$y=x$（即$w$第二维为0）拟合成了曲线$y=x+x^2$，在三维空间的表现形式就是平面$z=x$偏移到了$z=x+y$。
选取不同的阶数$p$时，多项式曲线如下图的红色曲线所示：
当我们达到更⾼阶的多项式$(p=9)$，我们得到了对于训练数据的⼀个完美的拟合。事实上，多项式函数精确地通过了每⼀个数据点，$L(w^{\ast })=0$。然⽽，拟合的曲线剧烈震荡，就表达函数$sin(2\pi x)$⽽⾔表现很差。这种⾏为叫做过拟合（over-fitting）。
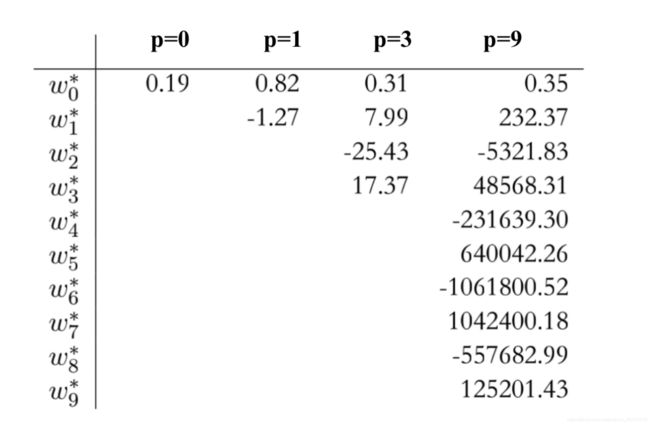
我们通过考察不同阶数多项式的系数$w^{\ast }$更深刻地思考这个问题，如下图所⽰，随着$M$的增⼤，系数的⼤⼩通常会变⼤。对于$M=9$的多项式，通过调节系数，让系数取相当⼤的正数或者负数，多项式函数可以精确地与数据匹配，但是对于数据之间的点(尤其是临近区间端点处的点)，从上图可以看到函数表现出剧烈的震荡。直觉上讲，发⽣了这样的事情：有着更⼤的M值的更灵活的多项式被过分调参，使多项式被调节成了与⽬标值的随机噪声相符。
当我们达到更⾼阶的多项式(p= 9)，我们得到了对于训练数据的⼀个完美的拟合。事实上，多项式函数精确地通过了每⼀个数据点，。然⽽，拟合的曲线剧烈震荡，就表达函数⽽⾔表现很差。这种⾏为叫做过拟合（over-fitting）。
我们通过考察不同阶数多项式的系数更深刻地思考这个问题，如下图所⽰，随着M的增⼤，系数的⼤⼩通常会变⼤。对于M = 9的多项式，通过调节系数，让系数取相当⼤的正数或者负数，多项式函数可以精确地与数据匹配，但是对于数据之间的点(尤其是临近区间端点处的点)，从上图可以看到函数表现出剧烈的震荡。直觉上讲，发⽣了这样的事情：有着更⼤的M值的更灵活的多项式被过分调参，使多项式被调节成了与⽬标值的随机噪声相符。

5. 过拟合解决方案

在实际应用时，如果样本容量不远远大于样本的特征维度，很可能造成过拟合，对这种情况，我们有下面四个解决方式：
1 加数据(会增大计算量)
2 特征选择（降低特征维度）如 PCA 算法。
3 正则化,限制系数的大小
4 贝叶斯（Bayesian）⽅法，参数的有效数量会⾃动根据数据集的规模调节，有效解决模型参数的数量超过数据点数量的情形。我们想针对模型参数w的合适选择进⾏强调和定量化。我们将会看到，从贝叶斯的观点来看，我们能够使⽤概率论来描述模型参数（例如w）的不确定性，或者模型本⾝的选择。

5.1.正则化

正则化一般是在损失函数（如最小二乘损失）上加入正则化项（表示模型的复杂度对模型的惩罚）$w=\underset{w}{\mathrm{argmin}}(L(w)+\lambda p(w)),\lambda >0$中$p(w)$是惩罚项
下面我们介绍一般情况下的两种正则化框架。

5.1.1. L1 Lasso

二维的$\lambda ||w|{|}_1$如下图所示：

可以看到，$\lambda ||w|{|}_1$是一个凸性很强的函数，原函数加上$\lambda ||w|{|}_1$可以增加原函数凸性从而更容易求解。因为$\lambda ||w|{|}_1$在坐标轴凸性最强，那么原函数加上$\lambda ||w|{|}_1$后在坐标轴位置凸性也增强，则最优解更容易迭代到坐标轴附近，即更容易获得稀疏解。

5.1.2.L2 Ridge

$$\begin{array}{rl}& \underset{w}{\mathrm{argmin}}L(w)s.t.||w|{|}_2^2\le C\\ & \hat{w}=\underset{w}{\mathrm{argmin}}[L(w)+\lambda w^{T}w]\\ & \frac{\partial }{\partial w}[L(w)+2\lambda w^{T}w]=2X^{T}X\hat{w}-2X^{T}Y+2\lambda \hat{w}=0\\ & \hat{w}=(X^{T}X+\lambda \mathbb{I}{)}^{-1}{X}^{T}Y\end{array}\text{\hspace{1em}(11)}$$二维的$\lambda ||w|{|}_2^2$如下图所示：
可以看到，$||w|{|}_1$与$||w|{|}_2^2$的不同就在于$||w|{|}_2^2$的凸性分布比较均匀，因此不太可能产生稀疏性解。
因此，$||w|{|}_1$会趋向于产生少量的特征，而其他的特征都是0，而$||w|{|}_2^2$会选择更多的特征，这些特征的权重系数都会接近于0。

5.2.权重先验也为高斯分布

5.2.1.MAP

参数w的极大似然估计并不涉及模型复杂度,它完全由数据大小控制。使用贝叶斯方法可以更好地处理模型复杂度和过拟合。贝叶斯估计有两个关键优势：1先验：我们可以通过在参数上放置先验来量化我们可能拥有的任何先验知识。例如，如果我们认为方差可能很小，我们会选择一个先前的概率质量较低的值。2 量化不确定性：我们不是得到参数W的的单一估计，而是完全后验分布，关于W的不同值的可能性。例如，数据点很少，我们的W不确定性将是非常高，这样我们会充分利用数据，得到非常广泛的后验和更宽的解释面。
贝叶斯规则的本质就是将我们已知的知识(先验)和世界上的证据相结合(似然)，以告诉我们有关世界状况的信息(后验)。
取先验分布$w\sim \mathcal{N}(0,{\Sigma }_p)$，则$p(w)=\frac{1}{(2\pi {)}^{\frac{p}{2}}|{\Sigma }_p{|}^{\frac{1}{2}}}\exp \{-\frac{1}{2}{w}^T{\Sigma }_p^{-1}w\}$。$Y$由$w,X$决定，$Y$未知的情况下$w,X$相互独立于是：
$$\begin{array}{rl}& \hat{w}=\underset{w}{\mathrm{argmax}}p(w|X,Y)=\underset{w}{\mathrm{argmax}}\frac{p(w,X,Y)}{p(X,Y)}=\underset{w}{\mathrm{argmax}}p(w,X,Y)\\ & =\underset{w}{\mathrm{argmax}}\log (p(Y|X,w)p(w|X)p(X))\\ & =\underset{w}{\mathrm{argmax}}\log (p(Y|X,w)p(w|X))\\ & =\underset{w}{\mathrm{argmax}}\log (p(Y|X,w)p(w))\\ & =\underset{w}{\mathrm{argmax}}(\log p(Y|X,w)+\log p(w))\\ & =\underset{w}{\mathrm{argmax}}(\sum _{i=1}^N\log (\frac{1}{\sqrt{2\pi }\sigma }exp\{-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\})+log(\frac{1}{(2\pi {)}^{\frac{p}{2}}|{\Sigma }_p{|}^{\frac{1}{2}}}\exp \{-\frac{1}{2}{w}^T{\Sigma }_p^{-1}w\}))\\ & =\underset{w}{\mathrm{argmax}}(\log (\frac{N}{\sqrt{2\pi }\sigma })+\sum _{i=1}^N\{-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\}+log(\frac{1}{(2\pi {)}^{\frac{p}{2}}|{\Sigma }_p{|}^{\frac{1}{2}}})+\{-\frac{1}{2}{w}^T{\Sigma }_p^{-1}w\})\\ & =\underset{w}{\mathrm{argmin}}(\sum _{i=1}^N\{\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\}+\{\frac{1}{2}{w}^T{\Sigma }_p^{-1}w\})\\ & =\underset{w}{\mathrm{argmin}}(\sum _{i=1}^N\{(y_i-w^T{x}_i{)}^2+\{{\sigma }^2{w}^T{\Sigma }_p^{-1}w\})\\ & =\underset{w}{\mathrm{argmin}}((Y^T-w^T{X}^T)(Y-Xw)+\{{\sigma }^2{w}^T{\Sigma }_p^{-1}w\})\\ & =\underset{w}{\mathrm{argmin}}(w^T{X}^{T}Xw-2w^{T}XY+{\sigma }^2{w}^T{\Sigma }_p^{-1}w)\end{array}$$
可得
$$\hat{w}=\underset{w}{\mathrm{argmin}}(w^T{X}^{T}Xw-2w^{T}XY+{\sigma }^2{w}^T{\Sigma }_p^{-1}w)\text{\hspace{1em}(12)}$$
我们将会看到，令${\Sigma }_p=I,{\sigma }^2=\lambda$，则(12)的第三项和和$L2$ Ridge 正则项对应，同样的如果将先验分布取为 Laplace 分布$f(x)=\frac{1}{2\alpha }exp\{-\frac{|x-\mu |}{\alpha }\}$（$\alpha ，\beta$为常数），那么就会得到和$L1$Lasso正则类似的结果。

5.2.2.贝叶斯估计

与MAP不同的是，MAP直接计算参数值，贝叶斯估计计算参数的分布，通过对分布求期望得到参数值。
对参数的后验分布进行推断：
$$\begin{array}{rl}p(w|X,Y)& =\frac{p(w,X,Y)}{p(X,Y)}\\ & =\frac{p(Y|w,X)p(w,X)}{p(X,Y)}\\ & =\frac{p(Y|w,X)p(w|X)}{p(Y|X)}\\ & =\frac{p(Y|w,X)p(w)}{\int p(w,Y|X)dw}\end{array}\text{\hspace{1em}(13)}$$
分母是常数，并不会影响到后验分布的均值与方差
$$p(w|X,Y)\propto \prod _{i=1}^N\mathcal{N}(y_i|w^T{x}_i,{\sigma }^2)\cdot \mathcal{N}(0,{\Sigma }_p)\text{\hspace{1em}(14)}$$已知共轭关系是指似然概率和先验概率的共轭，我们找到一个先验概率，如果后验概率与先验概率是一样的形式，那么该先验概率为似然函数的共轭先验，先验分布和后验分布是共轭分布。高斯分布符合上述分布的定义，可得(14)的后验分布也是一个高斯分布。
第一项：
$$\begin{array}{rl}\prod _{i=1}^N\mathcal{N}(y_i|w^T{x}_i,{\sigma }^2)& =\frac{1}{(2\pi {)}^{N/2}{\sigma }^N}\exp (-\frac{1}{2{\sigma }^2}\sum _{i=1}^N(y_i-w^T{x}_i{)}^2)\\ & =\frac{1}{(2\pi {)}^{N/2}|{\sigma }^2\mathbb{I}{|}^{\frac{N}{2}}}\exp (-\frac{1}{2}(Y^T-w^T{X}^T)({\sigma }^{-2}\mathbb{I})(Y-Xw))\\ & =\frac{1}{(2\pi {)}^{N/2}|{\sigma }^2\mathbb{I}{|}^{\frac{N}{2}}}\exp (-\frac{1}{2}(Y-Xw{)}^T({\sigma }^{-2}\mathbb{I})(Y-Xw))\\ & =\mathcal{N}(Xw,{\sigma }^2\mathbb{I})\end{array}\text{\hspace{1em}(15)}$$(15)代入(14)：$$p(w|X,Y)\propto \exp (-\frac{1}{2}(Y-Xw{)}^T{\sigma }^{-2}\mathbb{I}(Y-Xw)-\frac{1}{2}{w}^T{\Sigma }_p^{-1}w)\text{\hspace{1em}(16)}$$假定最后得到的高斯分布为：$\mathcal{N}({\mu }_w,{\Sigma }_w)$。对于(16)的分布，采用配方的方式来得到最终的分布:
指数上面的二次项为：$-\frac{1}{2{\sigma }^2}{w}^T{X}^{T}Xw-\frac{1}{2}{w}^T{\Sigma }_p^{-1}w$
于是：$${\Sigma }_w^{-1}={\sigma }^{-2}{X}^{T}X+{\Sigma }_p^{-1}=A\text{\hspace{1em}(17)}$$
一次项：$\frac{1}{2{\sigma }^2}2Y^{T}Xw={\sigma }^{-2}{Y}^{T}Xw={\mu }_w^T{\Sigma }_w^{-1}$
于是：$${\mu }_w={\sigma }^{-2}{A}^{-1}{X}^{T}Y\text{\hspace{1em}(18)}$$
于是：$$p(w|X,Y)\sim \mathcal{N}({\mu }_w,{\Sigma }_w)=\mathcal{N}({\sigma }^{-2}{A}^{-1}{X}^{T}Y,A^{-1})\text{\hspace{1em}(19)}$$
预测结果
给定一个$x^{\ast }$，求解$y^{\ast }$，我们有$y^{\ast }=x^{\ast T}w+{\sigma }^2$，已知 $p(w|X,Y)\sim \mathcal{N}({\mu }_w,{\Sigma }_w)$
代入条件高斯分布的公式可得：$$p(y^{\ast }|w,X,Y,x^{\ast })\sim \mathcal{N}(x^{\ast T}{\mu }_w,{\sigma }^2+x^{\ast T}{\Sigma }_w{x}^{\ast })\}\text{\hspace{1em}(20)}$$

5.2.3.置信区间

根据中心极限定理，对于任意均值$\mu$方差${\sigma }^2$的分布$p(X)$，若采样$n\ge 30$次，则$X\sim \mathcal{N}(n\mu ,n{\sigma }^2)$=>$\bar{X}\sim \mathcal{N}(\mu ,\frac{{\sigma }^2}{n})$=>$\frac{\bar{X}-\mu }{\frac{\sigma }{\sqrt{n}}}\sim \mathcal{N}(0,1)$

则求$p(X)$ 95%的置信区间，$\alpha =1-0.95=0.05$，可通过查表得$z_{\frac{\alpha }{2}}=z_{0.025}=1.96$，计算过程如下图

5.2.4.贝叶斯估计python实现

import  numpy as np
import matplotlib.pyplot as plt
import math
class Bayesian:
    def __init__(self,sigma,prior_mu,prior_sigma):
        self.sigma=sigma#噪声方差
        self.prior_mu=prior_mu#参数先验均值
        self.prior_sigma=prior_sigma#参数先验方差
    def fit(self,X,Y):
        if X.shape[1]==1:#一维情况
            A = 1 / (self.sigma ** 2) * np.dot(X.T, X) + 1/self.prior_sigma
            self.posterior_sigma = 1/A
            self.posterior_mu = 1/(self.sigma ** 2) * self.posterior_sigma * np.dot(X.T, Y)
        else:#多维情况
            A=1/(self.sigma**2)*np.dot(X.T,X)+np.linalg.inv(self.prior_sigma)
            self.posterior_sigma=np.linalg.inv(A)
            self.posterior_mu=1/(self.sigma**2)*self.posterior_sigma*np.dot(X.T,Y)
    def pre(self,x_star,confidence):
        self.n=1000
        mu=np.dot(x_star.T,self.posterior_mu)
        sigma=self.sigma**2+np.dot(x_star.T,self.posterior_sigma).dot(x_star)
        #我们每次预测返回一个置信度95%的区间
        return (mu - confidence * sigma / (math.sqrt(self.n)), mu + confidence * sigma / (math.sqrt(self.n)))
def generate(noise_sigma):
    X = np.linspace(-100, 100,10000).reshape(-1,1)#在[-100,100]均匀取10000个点
    w = np.array([3.6])
    Y = np.dot(X,w) + np.random.normal(0, noise_sigma, size=X.shape[0])##加上均值为0，标准差为nois_sigma的高斯分布
    return X,Y
if __name__=="__main__":
    noise_sigma=30#噪声方差
    confidence=1.96#置信度95%的区间对应的z为1.96
    X, Y = generate(noise_sigma)
    bay = Bayesian(noise_sigma, 0, 1)
    bay.fit(X, Y)
    y1,y2=[],[]
    for x in X[:,0]:
        R=bay.pre(x,confidence)
        y1.append(*R[0])
        y2.append(*R[1])
    plt.scatter(X, Y,c='black',label='Sample points',s=1)
    plt.plot(X,y1,color='red',label='95%confidence interval,sample 1000 times')
    plt.plot(X,y2,color='red')
    plt.legend()
    plt.show()

由于贝叶斯估计生成的是关于$y^{\ast }$的高斯分布，因此我们可以用置信区间表示其取值。

6.高斯过程回归

6.1.概述

将一维高斯分布推广到多变量中就得到了高斯网络，将多变量推广到无限维，就得到了高斯过程，高斯过程是定义在连续域（时间空间）上的无限多个高维随机变量所组成的随机过程。
在时间轴上的任意一个点n，有$y_n$服从高斯分布，且$(y_1,y_2,\cdots ,y_n)$服从$n$维高斯分布，那么随机过程$\{y_1,y_2,\cdots ,y_n\}$是一个高斯过程,$\{y_1,y_2,\cdots ,y_n\}$各取一个值值可以组成高斯过程的一个样本。
高斯过程有两个参数（高斯过程存在性定理），均值函数$m(n)=\mathbb{E}[y_n]$和协方差函数 $k(n_1,n_2)=\mathbb{E}[(y_{n_1}-\mathbb{E}[y_{n_1}])(y_{n_2}-\mathbb{E}[y_{n_2}])]$。
贝叶斯线性回归+核方法=高斯过程回归
高斯过程回归分为两种视角：
1.权空间的视角-核贝叶斯线性回归
2.函数空间的视角-高斯分布。
两者达到的效果一样。

6.2.权空间的视角-核贝叶斯线性回归

贝叶斯线性回归可以通过加入核函数的方法来解决非线性函数的问题，将$f(x)=x^{T}w$这个函数变为$f(x)=\varphi (x{)}^{T}w$（${\Sigma }_p$也要变为更高维度的），变换到更高维的空间，有：
$$f(y^{\ast })\sim \mathcal{N}({\sigma }^{-2}\varphi (x^{\ast }{)}^T{A}^{-1}{\Phi }^{T}Y,\varphi (x^{\ast }{)}^T{A}^{-1}\varphi (x^{\ast }))\text{\hspace{1em}(21)}$$其中，$\Phi =(\varphi (x_1),\varphi (x_2),\cdots ,\varphi (x_N){)}^T$，${\Sigma }_p$来自高斯先验：$p(w)=\mathcal{N}(0,{\Sigma }_p)$，${\sigma }^2$是噪声方差，$x^{\ast }$是输入的新数据。
计算均值：
$$\begin{array}{rl}& A={\sigma }^{-2}{\Phi }^T\Phi +{\Sigma }_p^{-1}\\ & \iff A{\Sigma }_p={\sigma }^{-2}{\Phi }^T\Phi {\Sigma }_p+\mathbb{I}\\ & \iff A{\Sigma }_p{\Phi }^T={\sigma }^{-2}{\Phi }^T\Phi {\Sigma }_p{\Phi }^T+{\Phi }^T={\sigma }^{-2}{\Phi }^T(k+{\sigma }^2\mathbb{I})\\ & \iff {\Sigma }_p{\Phi }^T={\sigma }^{-2}{A}^{-1}{\Phi }^T(k+{\sigma }^2\mathbb{I})\\ & \iff {\sigma }^{-2}{A}^{-1}{\Phi }^T={\Sigma }_p{\Phi }^T(k+{\sigma }^2\mathbb{I}{)}^{-1}\\ & \iff {\sigma }^{-2}\varphi (x^{\ast }{)}^T{A}^{-1}{\Phi }^T=\varphi (x^{\ast }{)}^T{\Sigma }_p{\Phi }^T(k+{\sigma }^2\mathbb{I}{)}^{-1}\end{array}$$
得到均值为：$$\mu =\varphi (x^{\ast }{)}^T{\Sigma }_p{\Phi }^T(k+{\sigma }^2\mathbb{I}{)}^{-1}Y\text{\hspace{1em}(22)}$$其中$k=\Phi {\Sigma }_p{\Phi }^T$。
计算方差：
先利用$(A+UCV{)}^{-1}=A^{-1}-A^{-1}U(C^{-1}+V{A}^{-1}U{)}^{-1}V{A}^{-1}$求解$A^{-1}$
所以$A^{-1}={\Sigma }_p-{\Sigma }_p{\Phi }^T({\sigma }^2\mathbb{I}+k{)}^{-1}\Phi {\Sigma }_p$
得到方差为：$$\Sigma =\varphi (x^{\ast }{)}^T{\Sigma }_p\varphi (x^{\ast })-\varphi (x^{\ast }{)}^T{\Sigma }_p{\Phi }^T({\sigma }^2\mathbb{I}+k{)}^{-1}\Phi {\Sigma }_p\varphi (x^{\ast })\text{\hspace{1em}(23)}$$
我们看到，在均值和方差中，含有下面四项：
$$\varphi (x^{\ast }{)}^T{\Sigma }_p{\Phi }^T,\varphi (x^{\ast }{)}^T{\Sigma }_p\varphi (x^{\ast }),\varphi (x^{\ast }{)}^T{\Sigma }_p{\Phi }^T,\Phi {\Sigma }_p\varphi (x^{\ast })$$上面四项的形式和$k(x,x^{\prime })=\varphi (x{)}^T{\Sigma }_p\varphi (x^{\prime })$是一样的。由于${\Sigma }_p$是正定对称的方差矩阵，所以，这是一个核函数$k(x,x^{\prime })=({\Sigma }_p^{\frac{1}{2}}\varphi (x){)}^T({\Sigma }_p^{\frac{1}{2}}\varphi (x^{\prime }))$，可令$\psi (x)={\Sigma }_p^{\frac{1}{2}}\varphi (x)$。因此高斯过程中的均值和方差全和核函数有关。这样就可以直接定义核函数而避免了求（核方法）。
高斯过程中的协方差：
给定先验$p(w)=\mathcal{N}(0,{\Sigma }_p)$
$\because f(x)=\varphi (x{)}^{T}w+ϵ$
$\therefore E[f(x)]=E[\varphi (x{)}^{T}w]=E[\varphi (x{)}^T]E[w]=0$
$$\begin{array}{rl}& k(n_1,n_2)=Cov[f(x),f(x^{\prime })]\\ & =E[(f(x)-E[f(x)])(f(x^{\prime })-E[f(x^{\prime })])]\\ & =E[f(x)f(x^{\prime })]\\ & =E[\varphi (x{)}^{T}w\varphi (x^{\prime }{)}^{T}w]\\ & =E[\varphi (x{)}^{T}w{w}^T\varphi (x^{\prime })]\\ & =\varphi (x{)}^{T}E[w{w}^T]\varphi (x^{\prime })\\ & =\varphi (x{)}^T(E[w{w}^T]-E[w{]}^{T}E[w])\varphi (x^{\prime })\\ & =\varphi (x{)}^T{\Sigma }_p\varphi (x^{\prime })\end{array}\text{\hspace{1em}(23)}$$可以看到，这就对应着上面的核函数。因此$f(x)$组成的一系列变量集合就是一个高斯过程。

6.3.函数空间的视角-高斯分布

相比权重空间，我们也可以直接关注$f$这个空间，对于预测任务，这就是类似于求：$p(y^{\ast }|X,Y,x^{\ast })={\int }_{f}p(y^{\ast }|f,X,Y,x^{\ast })p(f|X,Y,x^{\ast })df$
对于数据集来说，取
$f(X)\sim \mathcal{N}(\mu (X),k(X,X)),Y=f(X)+\epsilon \sim \mathcal{N}(\mu (X),k(X,X)+{\sigma }^2\mathbb{I})$
预测任务的目的是给定一个新数据序列$X^{\ast }=(x_1^{\ast },\cdots ,x_M^{\ast }{)}^T$，得到$Y^{\ast }=f(X^{\ast })+\epsilon$。我们可以写出:$$\left[\begin{array}{c}Y\\ f(X^{\ast })\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}\mu (X)\\ \mu (X^{\ast })\end{array}\right],\left[\begin{array}{cc}k(X,X)+{\sigma }^2\mathbb{I}& k(X,X^{\ast })\\ k(X^{\ast },X)& k(X^{\ast },X^{\ast })\end{array}\right]\right)$$
根据高斯分布的方法：
$$\begin{array}{rl}& x=\left[\begin{array}{c}{x}_a\\ x_b\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}{\mu }_a\\ {\mu }_b\end{array}\right],\left[\begin{array}{cc}{\Sigma }_{aa}& {\Sigma }_{ab}\\ {\Sigma }_{ba}& {\Sigma }_{bb}\end{array}\right]\right)x_b|x_a\sim \mathcal{N}({\mu }_{b|a},{\Sigma }_{b|a}){\mu }_{b|a}={\Sigma }_{ba}{\Sigma }_{aa}^{-1}(x_a-{\mu }_a)+{\mu }_b{\Sigma }_{b|a}={\Sigma }_{bb}-{\Sigma }_{ba}{\Sigma }_{aa}^{-1}{\Sigma }_{ab}\\ & p(f(X^{\ast })|X,Y,X^{\ast })=p(f(X^{\ast })|Y)\\ & =\mathcal{N}(k(X^{\ast },X)[k(X,X)+{\sigma }^2\mathbb{I}{]}^{-1}(Y-\mu (X))+\mu (X^{\ast }),k(X^{\ast },X^{\ast })-k(X^{\ast },X)[k(X,X)+{\sigma }^2\mathbb{I}{]}^{-1}k(X,X^{\ast }))\end{array}$$
所以对于：
$Y^{\ast }=f(X^{\ast })+\epsilon$
有$$p(Y^{\ast }|f(X^{\ast }))\sim \mathcal{N}(k(X^{\ast },X)[k(X,X)+{\sigma }^2\mathbb{I}{]}^{-1}(Y-\mu (X))+\mu (X^{\ast }),k(X^{\ast },X^{\ast })-k(X^{\ast },X)[k(X,X)+{\sigma }^2\mathbb{I}{]}^{1}k(X,X^{\ast })+{\sigma }^2\mathbb{I})$$我们看到，函数空间的观点更加简单易于求解。

7.小结

线性回归模型是最简单的模型，但是麻雀虽小，五脏俱全，在这里，我们利用最小二乘误差得到了闭式解。同时也发现，在噪声为高斯分布的时候，MLE 的解等价于最小二乘误差，而增加了正则项后，最小二乘误差加上 L2 正则项等价于高斯噪声先验下的 MAP解，加上 L1 正则项后，等价于 Laplace 噪声先验。我们也可以通过贝叶斯估计生成完整的后验分布。
传统的机器学习方法或多或少都有线性回归模型的影子：
线性模型往往不能很好地拟合数据，因此有三种方案克服这一劣势：
1.对特征的维数进行变换，例如多项式回归模型就是在线性特征的基础上加入高次项。
2.在线性方程后面加入一个非线性变换，即引入一个非线性的激活函数，典型的有线性分类模型如感知机。
3.对于一致的线性系数，我们进行多次变换，这样同一个特征不仅仅被单个系数影响，例如多层感知机（深度前馈网络）。
线性回归在整个样本空间都是线性的，我们修改这个限制，在不同区域引入不同的线性或非线性，例如线性样条回归和决策树模型。
线性回归中使用了所有的样本，但是对数据预先进行加工学习的效果可能更好（所谓的维数灾难，高维度数据更难学习），例如 PCA 算法和流形学习。

8.参考

[1]: bilibili shuhuai008 白板推导机器学习 https://space.bilibili.com/97068901/