Paper Information
Title:Variational Graph Auto-Encoders
Authors:Thomas Kipf, M. Welling
Soures:2016, ArXiv
Others:1214 Citations, 14 References
1 A latent variable model for graph-structured data
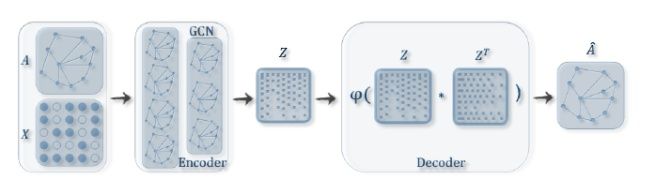
VGAE 使用了一个 GCN encoder 和 一个简单的内积 decoder ,架构如下图所示:
Definitions:We are given an undirected, unweighted graph $\mathcal{G}=(\mathcal{V}, \mathcal{E})$ with $N=|\mathcal{V}|$ nodes. We introduce an adjacency matrix $\mathbf{A}$ of $\mathcal{G}$ (we assume diagonal elements set to $1$ , i.e. every node is connected to itself) and its degree matrix $\mathbf{D}$ . We further introduce stochastic latent variables $\mathbf{z}_{i}$ , summarized in an $N \times F$ matrix $\mathbf{Z}$ . Node features are summarized in an $N \times D$ matrix $\mathbf{X}$ .
Inference model:使用一个两层的 GCN 推理模型
$q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})=\prod_{i=1}^{N} q\left(\mathbf{z}_{i} \mid \mathbf{X}, \mathbf{A}\right) \text { with } \quad q\left(\mathbf{z}_{i} \mid \mathbf{X}, \mathbf{A}\right)=\mathcal{N}\left(\mathbf{z}_{i} \mid \boldsymbol{\mu}_{i}, \operatorname{diag}\left(\boldsymbol{\sigma}_{i}^{2}\right)\right)$
其中:
-
- $\boldsymbol{\mu}=\operatorname{GCN}_{\boldsymbol{\mu}}(\mathbf{X}, \mathbf{A})$ is the matrix of mean vectors $\boldsymbol{\mu}_{i} $;
- $\log \boldsymbol{\sigma}=\mathrm{GCN}_{\boldsymbol{\sigma}}(\mathbf{X}, \mathbf{A})$;
def encode(self, x, adj):
hidden1 = self.gc1(x, adj)
return self.gc2(hidden1, adj), self.gc3(hidden1, adj)
mu, logvar = self.encode(x, adj)
GCN 的第二层分别输出 mu,log $\sigma$ 矩阵,共用第一层的参数。
这里 GCN 定义为:
$\operatorname{GCN}(\mathbf{X}, \mathbf{A})=\tilde{\mathbf{A}} \operatorname{ReLU}\left(\tilde{\mathbf{A}} \mathbf{X} \mathbf{W}_{0}\right) \mathbf{W}_{1}$
其中:
-
- $\mathbf{W}_{i}$ 代表着权重矩阵
- $\operatorname{GCN}_{\boldsymbol{\mu}}(\mathbf{X}, \mathbf{A})$ 和 $\mathrm{GCN}_{\boldsymbol{\sigma}}(\mathbf{X}, \mathbf{A})$ 共享第一层的权重矩阵 $\mathbf{W}_{0} $
- $\operatorname{ReLU}(\cdot)=\max (0, \cdot)$
- $\tilde{\mathbf{A}}=\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}$ 代表着 symmetrically normalized adjacency matrix
至于 $z$ 的生成:
def reparameterize(self, mu, logvar):
if self.training:
std = torch.exp(logvar)
eps = torch.randn_like(std)
return eps.mul(std).add_(mu)
else:
return mu
z = self.reparameterize(mu, logvar)
Generative model:我们的生成模型是由潜在变量之间的内积给出的:
$p(\mathbf{A} \mid \mathbf{Z})=\prod_{i=1}^{N} \prod_{j=1}^{N} p\left(A_{i j} \mid \mathbf{z}_{i}, \mathbf{z}_{j}\right) \text { with } p\left(A_{i j}=1 \mid \mathbf{z}_{i}, \mathbf{z}_{j}\right)=\sigma\left(\mathbf{z}_{i}^{\top} \mathbf{z}_{j}\right)$
其中:
-
- $\mathbf{A}$ 是邻接矩阵
- $\sigma(\cdot)$ 是 logistic sigmoid function.
class InnerProductDecoder(nn.Module):
"""Decoder for using inner product for prediction."""
def __init__(self, dropout, act=torch.sigmoid):
super(InnerProductDecoder, self).__init__()
self.dropout = dropout
self.act = act
def forward(self, z):
z = F.dropout(z, self.dropout, training=self.training)
adj = self.act(torch.mm(z, z.t()))
return adj
self.dc = InnerProductDecoder(dropout, act=lambda x: x)
adj = self.dc(z)
Learning:优化变分下界 $\mathcal{L}$ 的参数 $W_i$ :
$\mathcal{L}=\mathbb{E}_{q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})}[\log p(\mathbf{A} \mid \mathbf{Z})]-\mathrm{KL}[q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A}) \| p(\mathbf{Z})]$
其中:
-
- $\operatorname{KL}[q(\cdot) \| p(\cdot)]$ 代表着 $q(\cdot)$ 和 $p(\cdot)$ 之间的 KL散度。
- 高斯先验 $p(\mathbf{Z})=\prod_{i} p\left(\mathbf{z}_{\mathbf{i}}\right)=\prod_{i} \mathcal{N}\left(\mathbf{z}_{i} \mid 0, \mathbf{I}\right)$
def loss_function(preds, labels, mu, logvar, n_nodes, norm, pos_weight):
cost = norm * F.binary_cross_entropy_with_logits(preds, labels, pos_weight=pos_weight)
# see Appendix B from VAE paper:
# Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
# https://arxiv.org/abs/1312.6114
# 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
KLD = -0.5 / n_nodes * torch.mean(torch.sum(
1 + 2 * logvar - mu.pow(2) - logvar.exp().pow(2), 1))
return cost + KLD
Non-probabilistic graph auto-encoder (GAE) model
计算表示向量 $Z$ 和重建的邻接矩阵 $\hat{\mathbf{A}}$
$\hat{\mathbf{A}}=\sigma\left(\mathbf{Z Z}^{\top}\right), \text { with } \quad \mathbf{Z}=\operatorname{GCN}(\mathbf{X}, \mathbf{A})$
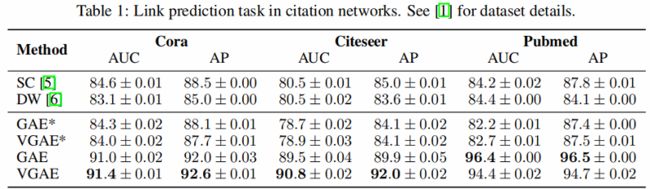
2 Experiments on link prediction
引文网络中链接预测任务的结果如 Table 1 所示。
GAE* and VGAE* denote experiments without using input features, GAE and VGAE use input features.