算法--贪心算法
贪心算法
1、贪心算法分析
1.1、什么是贪心算法
顾名思义,贪心算法或贪心思想采用贪心的策略,保证每次操作都是局部最优的,从而使最
后得到的结果是全局最优的。
找到一个比较的区间,然后找出区间最优解
1.2、贪心算法存在的问题
- 不能保证求得的最后解是最佳的;
- 不能用来求最大或最小解问题;
- 只能求满足某些约束条件的可行解的范围。
1.3、贪心算法一般流程
- 评价最优条件是什么?
- 循环 -> 未解决问题 && 还有解
- 从可能的解中取出最优解
- 执行最优解
- 缩小问题规模 -> 双指针, for循环 ,减去最优解…
2、LeetCode-455.分发饼干(简单)
455. 分发饼干
2.1、题目描述
2.2、示例
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
2.3、算法思想
这里的贪心策略是,给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。
至于具体实现,因为我们需要获得大小关系,一个便捷的方法就是把孩子和饼干分别排序。
这样我们就可以从饥饿度最小的孩子和大小最小的饼干出发,计算有多少个对子可以满足条件。
2.4、优化代码
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count=0;
int j=0; //饼干数组下标
int i=0; //孩子数组下标
while(i<g.length&&j<s.length){
if(s[j]>=g[i]){
count++;
i++;
}
j++;
}
return count;
}
}
3、LeetCode-135.分发糖果(困难)
135. 分发糖果
3.1、题目描述
3.2、示例
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
3.3、算法思想
做完了题目 455,你会不会认为存在比较关系的贪心策略一定需要排序或是选择?虽然这一
道题也是运用贪心策略,但我们只需要简单的两次遍历即可:把所有孩子的糖果数初始化为 1;
先从左往右遍历一遍,如果右边孩子的评分比左边的高,则右边孩子的糖果数更新为左边孩子的
糖果数加 1;再从右往左遍历一遍,如果左边孩子的评分比右边的高,且左边孩子当前的糖果数
不大于右边孩子的糖果数,则左边孩子的糖果数更新为右边孩子的糖果数加 1。通过这两次遍历,
分配的糖果就可以满足题目要求了。这里的贪心策略即为,在每次遍历中,只考虑并更新相邻一
侧的大小关系。
3.4、优化代码
//使用数组时间更快
class Solution {
public int candy(int[] ratings) {
int res = 0;
int length = ratings.length;
int[] temp = new int[length];
for(int i = 0; i < length; i++){
temp[i] = 1; //把所有孩子的糖果数初始化为 1
}
//如果右边孩子的评分比左边的高,则右边孩子的糖果数更新为左边孩子的糖果数加 1
for(int i = 0; i<length-1; i++){
if(ratings[i] > ratings[i+1]){
temp[i] = temp[i+1] + 1;
}
}
//注意:左边孩子当前的糖果数不大于右边孩子的糖果数
for(int j = length-1; j > 0; j--){
if(ratings[j] > ratings[j+1] && temp[j] <= temp[j-1]){
temp[j] = temp[j-1] + 1;
}
}
for(int item : temp){
res += item;
}
return res;
}
}
3.5、细节分析
要从数组的边界值开始判断
这样能避免少值判断
4、LeetCode-435.无重叠区间(中等)
435. 无重叠区间
4.1、题目描述
4.2、示例
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
3.3、算法思想
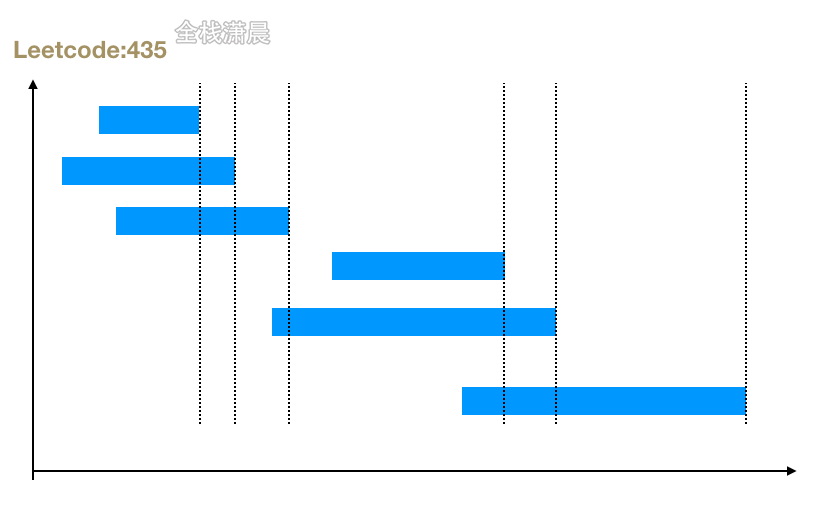
1.贪心思想:移除区间的最小数量需要确保前面区间最小影响后面区间,所以按照右端点排序两两比较移除影响后面大的即右端点大的那一个
2.关于为什么是按照区间右端点排序?
官解里对这个描述的非常清楚了,这个题其实是预定会议的一个问题,给你若干时间的会议,然后去预定会议,那么能够预定的最大的会议数量是多少?核心在于我们要找到最大不重叠区间的个数。 如果我们把本题的区间看成是会议,那么按照右端点排序,我们一定能够找到一个最先结束的会议,而这个会议一定是我们需要添加到最终结果的的首个会议。(这个不难贪心得到,因为这样能够给后面预留的时间更长)。
3.关于为什么是不能按照区间左端点排序?
这里补充一下为什么不能按照区间左端点排序。同样地,我们把本题的区间看成是会议,如果“按照左端点排序,我们一定能够找到一个最先开始的会议”,但是最先开始的会议,不一定最先结束。。举个例子:
|————| 区间a
|——| 区间b
|——| 区间c
|——————| 区间d
区间a是最先开始的,如果我们采用区间a作为放入最大不重叠区间的首个区间,那么后面我们只能采用区间d作为第二个放入最大不重叠区间的区间,但这样的话,最大不重叠区间的数量为2。但是如果我们采用区间b作为放入最大不重叠区间的首个区间,那么最大不重叠区间的数量为3,因为区间b是最先结束的。
4.如果一定要从左边排序,后面需要加一个判断条件
Arrays.sort(intervals,new Comparator<int[]>(){
public int compare(int[] a,int[] b){
return a[0]-b[0];
}
});
int right = intervals[0][1];
for(int i=1;i<n;i++){
if(intervals[i][0]<right){
count++;
}else{
right = intervals[i][1];
}
right=Math.min(right,intervals[i][1]);
//判断条件
//具体情况见452题分析
}
4.4、优化代码
//注意 需要根据实际情况判断按区间开头排序还是按区间结尾排序。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
int count = 0;
Arrays.sort(intervals, new Comparator<int[]>(){
public int compare(int[] a, int[] b){
return a[1] - b[1];
}
});
int pre = intervals[0][1];
for(int i = 1; i < intervals.length; i++){
if(intervals[i][0] < pre){ //区间结尾大就排除
count++;
}else{
pre = intervals[i][1];
}
}
return count;
}
}
5、LeetCode-605.种花问题(简单)
605. 种花问题
5.1、题目描述
5.2、示例
输入:flowerbed = [1,0,0,0,1], n = 1
输出:true
输入:flowerbed = [1,0,0,0,1], n = 2
输出:false
5.3、算法思想
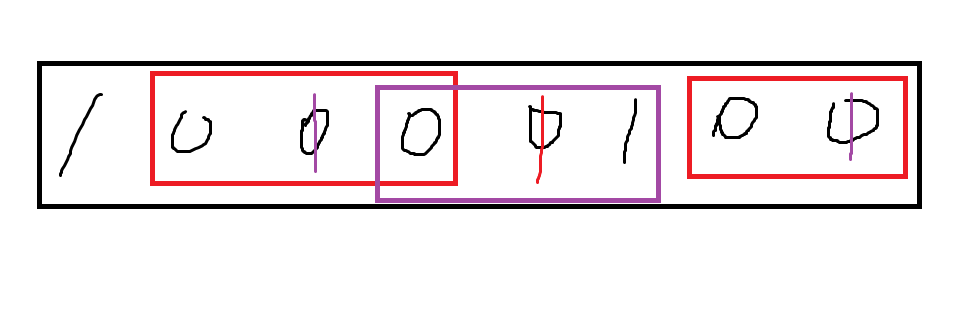
花不能种植在相邻的地块上,所以要种一束花至少要三块空地,即数组中有三个连续的0。因此,我们采取的贪心策略为,出现三个连续的0即种一束花。
注意:最后统计可用空地为2块时,即代表可以在最后一块空地上种一束花。
5.4、优化代码
class Solution {
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int length = flowerbed.length;
int count = 1; //假设在数组左边添加0,以解决边界问题,令count初始为1
for(int i = 0; i < length && n > 0; i++){ //当n==0时,没有花种了
if(flowerbed[i] == 0){
count++;
}else{
count = 0;
}
if(count == 3){ //每连续三个0种一次花
n--;
count = 1; //连续三个0出现,其最后一个0可作为下一次统计的初始值
}
}
if(count == 2){ //如果最后count为2而不是1,表示最后一个位置可以种花
n--;
}
return n <= 0;
}
}
5.5 自己思路
两两判断,如果前面一个数字为1,说明他的旁边不能种要跳过所以i++;
class Solution {
public boolean canPlaceFlowers(int[] flowerbed, int n) {
if(flowerbed.length == 1 && n<=1 && flowerbed[0]==0){
return true;
}
int count=0;
for(int i=1;i<flowerbed.length-1;i++){
if(flowerbed[i-1]==0 && flowerbed[i]==0){
//两处为0可以种花
flowerbed[i-1]=1;
count++;
}
if(flowerbed[i-1]==1){
i++;//前面已经种花,该处不能种花,跳过
}
}
if(flowerbed[flowerbed.length-1]==0 && flowerbed[flowerbed.length-2]==0) count++;
//最后两位都为0可以种花
return count>=n;
}
}
`
6、LeetCode-452. 用最少数量的箭引爆气球(中等)
用最少数量的箭引爆气球
6.1、题目描述
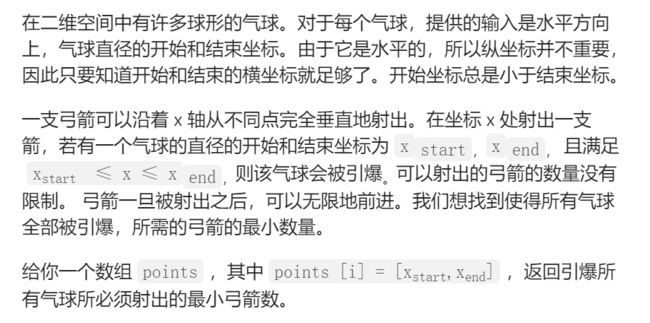
6.2、示例
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
6.3、算法思想
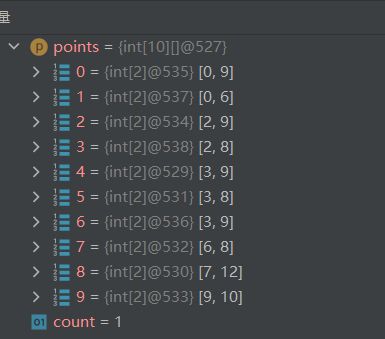
贪心法, 每个气球只少需要一支箭, 先按照右端点排序, 然后每次从最小的右端点射出一支箭, 去掉被射爆的气球, 重复该过程.
注意: 最近新增了Test Case, [[-2147483646,-2147483645],[2147483646,2147483647]] 就过不了了,这是因为差值过大而产生溢出。sort的时候不要用a-b来比较,要用Integer.compare(a, b)!!! 。
从左边开始判断:不能仅仅判断pre和points{i}{0}的值,需要在判断的同时,缩小边界。
若pre>points{i}{0}而且pre>points{i}{1},说明边界要变成points{i}{0},points{i}{1}
6.4、优化代码
//和435题类似
//从右边排序
class Solution {
public int findMinArrowShots(int[][] points) {
if(points.length == 1){
return 1;
}
Arrays.sort(points, new Comparator<int[]>(){
public int compare(int[] a, int[] b){
return Integer.compare(a[1], b[1]);
}
});
int pre = points[0][1];
int count = 1;
for(int i = 1; i < points.length; i++){
if(points[i][0] <= pre){
pre = Math.min(points[i][1], pre);
}else{
count++;
pre = points[i][1];
}
}
return count;
}
}
//从左边排序
class Solution {
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, (o1, o2) -> Integer.compare(o1[0], o2[0]));
int count = 1;
int n = points.length;
int pre = points[0][1];
for(int i=1;i<n;i++){
if(pre < points[i][0]){
count++;
pre = points[i][1];
}
pre = Math.min(pre,points[i][1]);
}
return count;
}
}
7、LeetCode-763. 划分字母区间(中等)
763. 划分字母区间
7.1、题目描述
7.2、示例
输入:S = "ababcbacadefegdehijhklij"
输出:[9,7,8]
解释:
划分结果为 "ababcbaca", "defegde", "hijhklij"。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
7.3、算法思想
字母问题首先想到是否需要用到下标,需要用到下标问题可以转换成存入26个空格的数组记录每一个字母出现的位置。
7.4、优化代码
class Solution {
public List<Integer> partitionLabels(String s) {
List<Integer> list = new ArrayList<>();
int[] last = new int[26]; //一共只有a~z 26个字母
char[] chars = s.toCharArray(); //转换成char数组查询更快
for(int i = 0; i < chars.length; i++){
last[chars[i] - 'a'] = i; //得到每个字母的最后一次出现的索引处
}
int firstIndex = 0;
int lastIndex = -1;
for(int j = 0; j < chars.length; j++){
lastIndex = Math.max(lastIndex, last[chars[j] - 'a']); //取当前区间内字母出现的最大索引
if(j == lastIndex){ //区间访问完
list.add(lastIndex - firstIndex + 1);
firstIndex = j + 1;
}
}
return list;
}
}
for(int i = 0; i < chars.length; i++){
last[chars[i] - 'a'] = i; //得到每个字母的最后一次出现的索引处
}
int firstIndex = 0;
int lastIndex = -1;
for(int j = 0; j < chars.length; j++){
lastIndex = Math.max(lastIndex, last[chars[j] - 'a']); //取当前区间内字母出现的最大索引
if(j == lastIndex){ //区间访问完
list.add(lastIndex - firstIndex + 1);
firstIndex = j + 1;
}
}
return list;
}
}