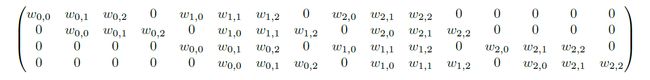深度学习中的各种卷积总结
- 深度学习中的各种卷积总结
-
- 01 普通卷积(Convolution)
-
- A. 普通卷积的计算操作
- B. 特殊的普通卷积
-
- B1.用途广泛的1x1卷积
- B2.卷积都是奇数的、nxn的么?
- 02 转置卷积/反卷积(Transposed convolution)
-
- A.转置卷积/反卷积的计算操作
- B.转置卷积/反卷积有什么作用?
- 03 空洞卷积/膨胀卷积(Dilated convolution)
-
- A.空洞卷积/膨胀卷积的计算操作
- B.空洞卷积/膨胀卷积有什么作用?
深度学习中的各种卷积总结
在深度学习中,卷积是一个非常重要的概念,卷积也是卷积神经网络拥有良好的图像处理能力的关键。这篇文章将介绍一下不同类型的卷积,为了简单起见,本文只关注于二维的卷积。首先我们先回忆一下卷积的基本概念:
卷积核大小(Kernel Size):卷积核的大小定义了卷积操作的感受野。在二维卷积中,通常设置为3,即卷积核大小为3×3。
步长(Stride):定义了卷积核遍历图像时的步幅大小。其默认值通常设置为1,也可将步幅设置为2后对图像进行下采样,这种方式与最大池化类似。
填充(Padding):定义了网络层处理样本边界的方式。当卷积核大于1且不进行边界扩充,输出尺寸将相应缩小;当卷积核以标准方式进行边界扩充,则输出数据的空间尺寸将与输入相等。
输入和输出通道(Channel):构建卷积层时需定义输入通道 I I I,并由此确定输出通道 O O O。这样,可算出每个网络层的参数量为 I ∗ O ∗ K I*O*K I∗O∗K,其中 K K K为卷积核的参数个数。例如,某个网络层有64个大小为3×3的卷积核,则对应 K K K值为 3×3 =9。
参考论文:
01 Paper: A guide to convolution arithmetic for deep learning
02 Paper:Multi-Scale Context Aggregation by Dilated Convolutions
卷积动画:
https://github.com/vdumoulin/conv_arithmetic
01 普通卷积(Convolution)
A. 普通卷积的计算操作
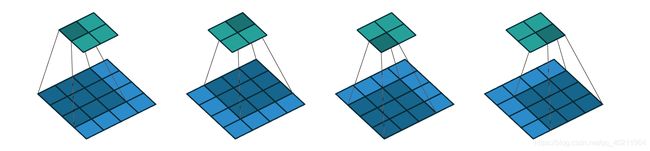
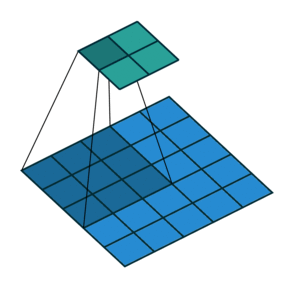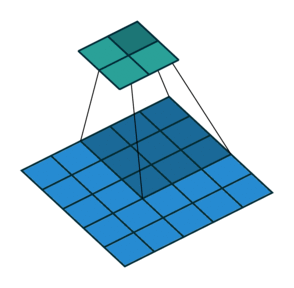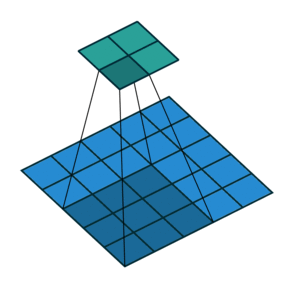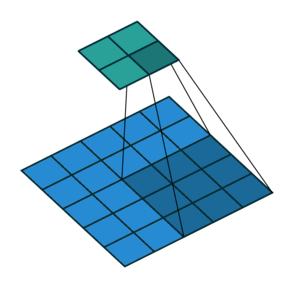
如图所示卷积是一个相当简单的操作:从卷积核开始,这是一个小的权值矩阵。这个卷积核在 输入数据上“滑动”,对当前输入的部分元素进行矩阵乘法,然后将结果汇为feature map。
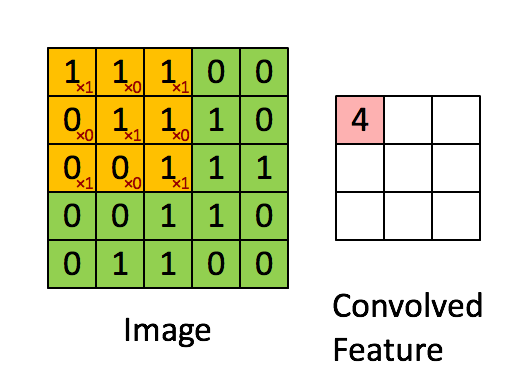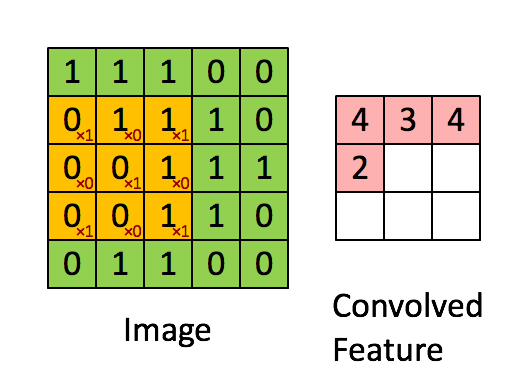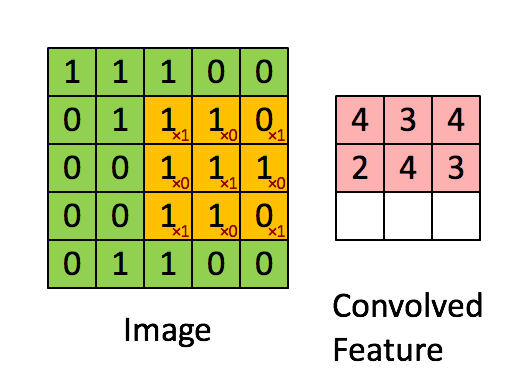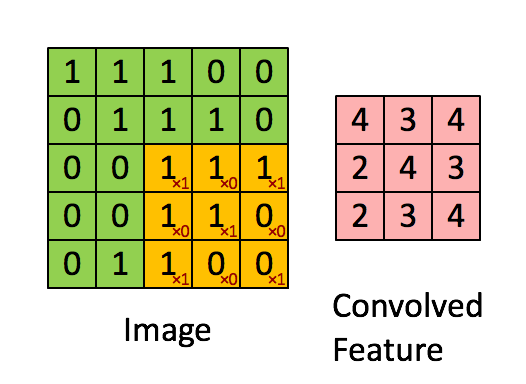
▽ \bigtriangledown ▽ 卷积核大小为3、步长为2、填充为0的二维卷积(蓝色为输入,绿色为输出)
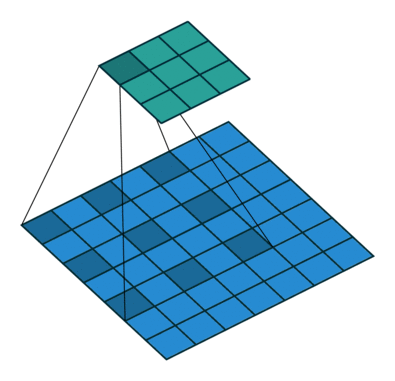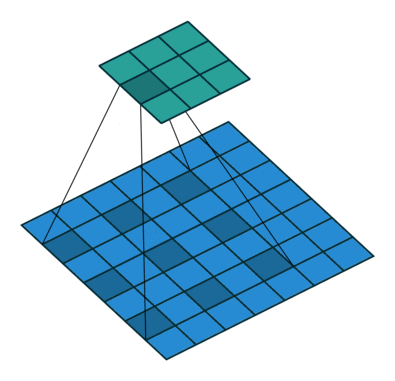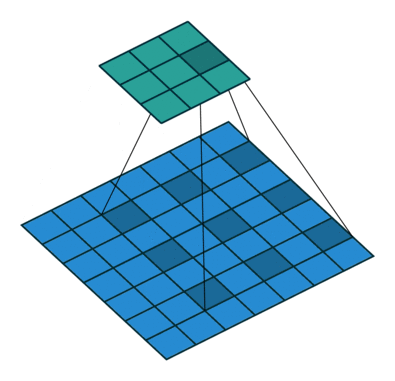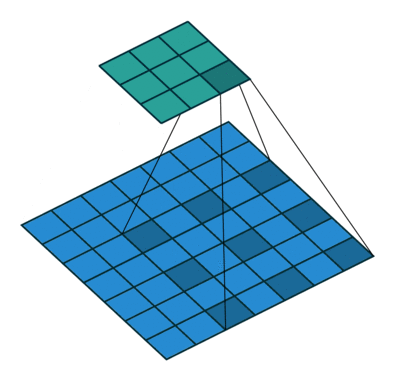
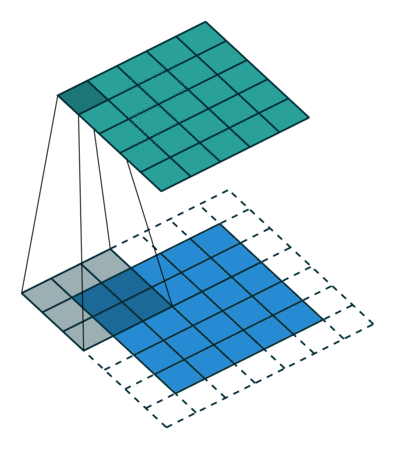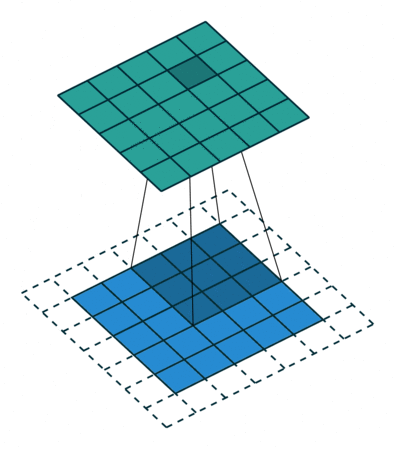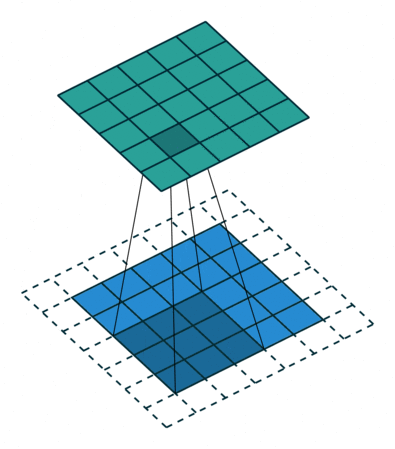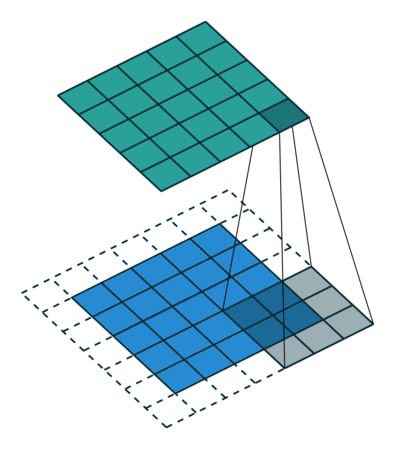
▽ \bigtriangledown ▽ 卷积核大小为3、步长为1、填充为1的二维卷积
B. 特殊的普通卷积
B1.用途广泛的1x1卷积
1x1的卷积核由于大小只有1x1,所以并不需要考虑像素跟周边像素的关系,它并不改变feature map的尺寸,它能够改变的只是通道数,对不同的通道上的像素点进行线性组合,然后进行非线性化操作。基于这一点,1x1卷积有着一些奇妙且实用的作用:
- 升维/降维
所谓升维/降维,就是增加/减少通道数。如下图所示,使用2个1x1大小的卷积核,那么feature map的通道数将会从3变成2,如果使用4个1x1的卷积核,feature map的通道数将会由3变成4。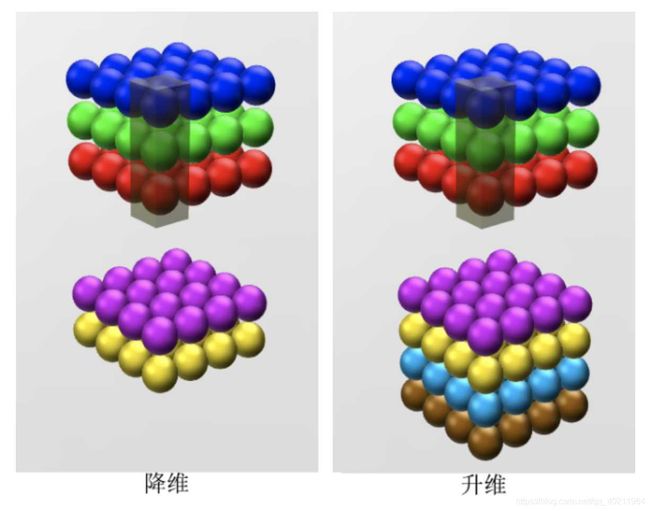
- 通道间的信息聚合
升维/降维的意义再往深处想,就是能实现通道之间的信息聚合。Think about that:使用1x1卷积核,实现升维和降维的操作其实就是通道间信息的线性组合变化。比如,Feature Map 大小是256x256x3,卷积核大小3x3x3,数量为64,假设步长为2,Feature Map就变成了128x128x64;后面添加一个1x1x64,数量为32的卷积核,Feature Map就变成了128x128x28,原来的64个channels就可以理解为跨通道线性组合变成了28channels,这实现通道间的信息交互及融合。 - 减少参数
前面所说的降维,其实也是减少了参数,因为feature map的通道数少了,参数也自然跟着就减少,相当于先压缩特征图,二次提取特征,使得新特征图的特征表达更佳(去除掉了冗余的信息)。 - 增加非线性
因为1*1卷积核后接了非线性激活函数,就可以可以在保持feature map尺寸不变(即不损失分辨率)的前提下大幅增加非线性特性,把网络做的很deep,使网络学习到更复杂的模式。
B2.卷积都是奇数的、nxn的么?
我们现在关注的是cv领域的,大多接触的卷积核是正方形,比如说5x5,3x3,1x1的卷积核大小,那么卷积核都是正方形的么?都是奇数的么?有没有其他的卷积核大小?要回答这些问题,我们需要一步步的来~
【为什么认为卷积操作是有效的?】
除了大量的实验数据可以证明卷积操作是有效的以外,实际上我们是无法破解为什么卷积是真的可以work的,但是我们可以从一些角度去推测卷积有效的可能原因。首先,卷积操作的第一个灵感来源或者基础就是仿生,模仿人眼对于事物的感知,人眼对于事物的感知是整片区域,并且可以理解为一个神经元来负责理解,这也就是说每个感受野要有一个输出,这就类似于卷积操作;其次,卷积操作的第二个基础就是假设,如果说在同一张图片上,人可以辨认出狗头,那么也可以辨认出狗腿,所以,当卷积核或者滤波器遍历图像的时候,要求此卷积核又要认识狗头又要认识狗腿,就要求卷积核要共享权重。
【为什么大多使用3x3的卷积核?】
个人认为,3x3的卷积核是可以考虑到目标点周围8个方向上的信息(上/下/左/右/左上/左上/右下/右上),并且比5x5的卷积计算量要小,因为可以用两个3x3的卷积来代替1个5x5的卷积(但是,如果你在计算资源允许的情况下,浅层特征要较大的感受野的话推荐使用5x5,也是具体问题具体分析)。
【为什么卷积核大多是正方形的?有矩形的卷积核么?】
卷积核不只是有正方形的,也有矩形的,例如非对称卷积的卷积核就是1xn或者nx1;此外,在nlp领域中常用的就是矩形卷积。是用矩形卷积还是正方形卷积也是具体问题具体分析,在通常的cv领域中,我们可以都使用正方形的卷积,因为人眼的感受区域是圆形,越接近人眼仿生的卷积越能捕捉到图像特征;但是在一些特定的单类别检测或者特征提取中,如果被检测或者被提取的物体呈现出了统一的矩形形状特点,也可以尝试使用矩形卷积捕捉这种特性。
02 转置卷积/反卷积(Transposed convolution)
我们一般可以通过卷积操作来实现高维特征到低维特征的转换,而如果想要将这一过程反过来,即由低维特征恢复到高维特征,我们可以借由转置卷积来实现。之所以叫转置卷积是因为,它其实是把我们平时所用正常卷积操作中的卷积核做一个转置,然后把正常卷积的输出作为转置卷积的输入,而转置卷积的输出,就是正常卷积的输入。
A.转置卷积/反卷积的计算操作
那么具体怎么实现的呢,让我们先来将正常卷积换一个写法:
这是一个4x4的输入,经过一个3x3的卷积核(步长为1,填充为0),得到的是2x2的输出。
本来输入输出都是矩阵的形式,现在我们把他们变成向量的形式,也就是把输入reshape成16x1,把输出reshape成4x1。那么相应的,想要由16x1的输入得到4x1的输出,卷积核就得变成4x16的。我们就可以把卷积核写成这个亚子:
用 x , C , z x,C, z x,C,z分别表示变换之后的输入、卷积核和输出,那么正常卷积就可以这样写: z = C x z = Cx z=Cx
这个就是正常卷积的过程:由输入和卷积核得到输出。
那么反过来由输出和卷积核的转置就能得到输入: x = C T z x = C^Tz x=CTz
这就是转置卷积的由来。
让我们来看几个例子:
-
首先是正常卷积步长s=1的时候,其对应的转置矩阵卷积核大小不变的情况下,我们可以通过填充来实现转置卷积。
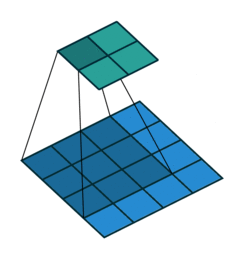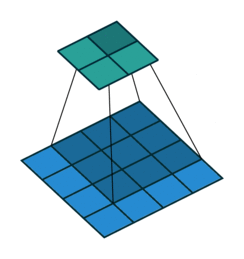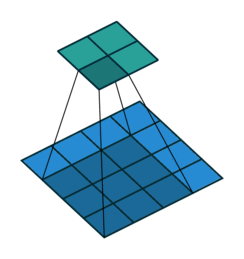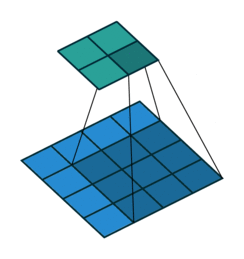
▽ \bigtriangledown ▽ 卷积核大小为3×3、步长为1和无填充的正常卷积;输入为4x4,输出为2x2
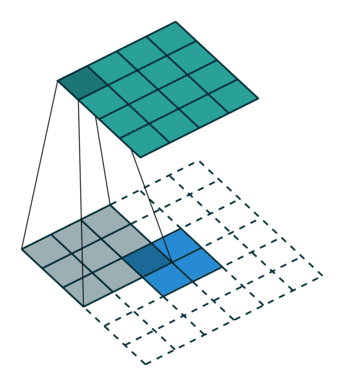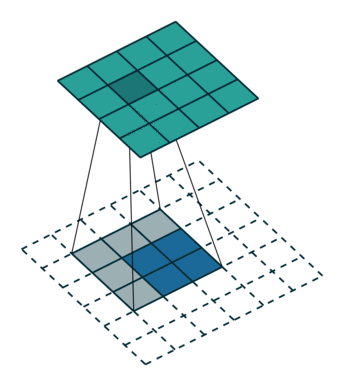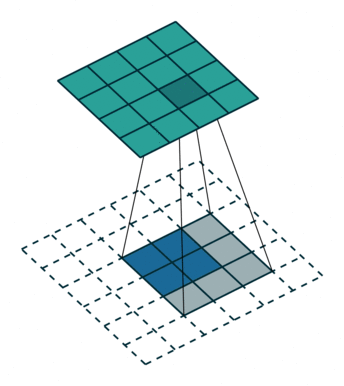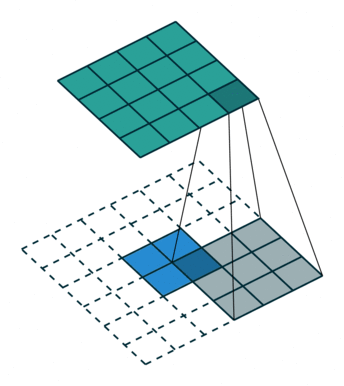
- 如果正常卷积步长为s>1时,希望其对应的转置卷积步长为 1 s \frac{1}{s} s1,我们需要在输入中插入s-1个0来实现转置矩阵的步长s<1的效果。步长s<1的转置卷积也称为微步卷积(Fractionally-strided convolution)。
▽ \bigtriangledown ▽ 卷积核大小为3×3、步长为2和无填充的正常卷积;输入为5x5,输出为2x2

▽ \bigtriangledown ▽ 卷积核大小为3×3、步长为1/2和填充为2的转置卷积;输入为2x2,输出为5x5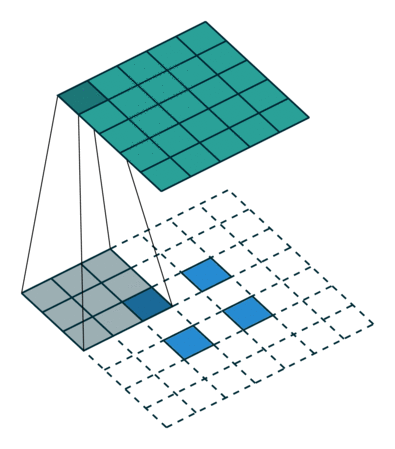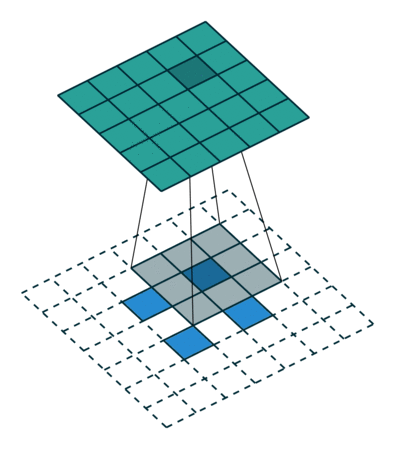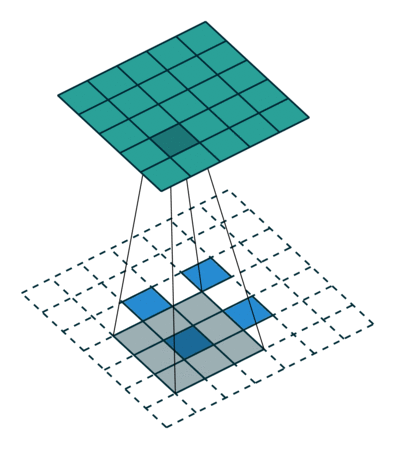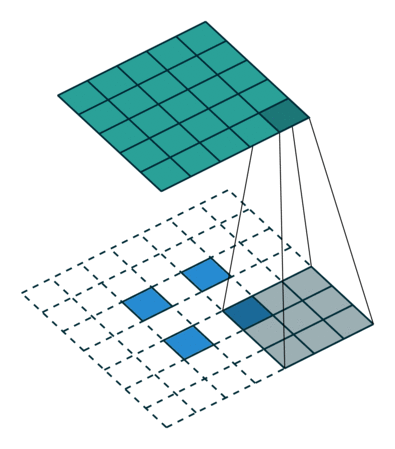
注意的是:其实严格意义上转置卷积不是反卷积。
反卷积在数学含义上是可以完全还原输入信号的是卷积的逆过程;但是转置卷积只能还原到原来输入的shape,重建先前的空间分辨率,执行了卷积操作,其value值是不一样的,并不是卷积的数学逆过程。
但是应用于编码器-解码器结构中,转置矩阵仍然很有用。这样转置卷积就可以同时实现图像的粗粒化(upscaling)和卷积操作,而不是通过两个单独过程来完成了。并且转置卷积常常用于CNN中对特征图进行上采样,比如语义分割和超分辨率任务中。
B.转置卷积/反卷积有什么作用?
转置卷积/反卷积可以认为是步长为分数的卷积操作,最直观的感受可以实现上采样,在ZFNet中,转置卷积/反卷积被用作特征的可视化,在SRCNN/FSRCNN中,转置卷积/反卷积被用作了上采样图像,成为超分(SR)中的一小步,转置卷积/反卷积的作用还是很多的。
03 空洞卷积/膨胀卷积(Dilated convolution)
空洞卷积(又名膨胀卷积),是一种不增加参数数量,但却增加感受野的特殊卷积。它通过给卷积核插入“空洞”来变相地增加其大小,只是引入了一个称为 “膨胀率(dilation rate)”的超参数。
A.空洞卷积/膨胀卷积的计算操作
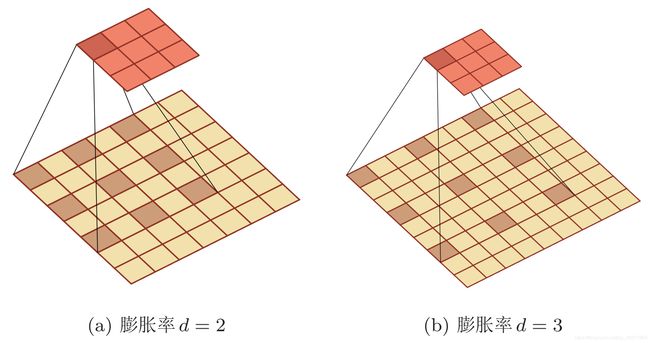
如果膨胀率为d,那么就会在卷积核的每两个元素之间插入d-1个空洞。当d=1时卷积核为普通的卷积核。
▽ \bigtriangledown ▽ 卷积核大小为3、步长为1、填充为0、膨胀率为2的二维卷积
B.空洞卷积/膨胀卷积有什么作用?
在相同的计算条件下,空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野,但计算资源有限而无法提高卷积核数量或大小时,可以考虑空洞卷积。
我们对于深度学习还在不断摸索中,如果在学习过程中遇到了特殊的卷积操作会不断的补充上来。也给实验室的师弟们师妹们打call,即使放假了还在不断学习和分享,我们仍是深度学习的小学生,请大家多多指教!