数据结构之二叉树的遍历

     这篇文章是看完《学习JavaSscript数据结构与算法》写的总结，主要是记一下在我在书中遇到的难点、以及一些可能不太难，但理解起来会比较绕的点，供大家参考学习，也让自己能够复习巩固一遍，本文后半部分结合面试题讲解。

二叉树的遍历

     首先我们要构建一棵二叉树，然后以构建的这棵二叉树为例讲解它的三种遍历方式，大家可以以此对比三种遍历方式到底是哪里不一样。

     开始构建上图的这棵二叉树

const tree = new BinarySearchTree()
tree.insert(8) // 根结点

tree.insert(2)
tree.insert(9)
tree.insert(3)

console.log(tree)

     构建完成，打印一下，在控制台看一下它的结构是否是正确的

     能够看到，这棵树的结构是正确的，所以让我们开始学习二叉树的遍历吧

①先序遍历

     先序遍历（前序遍历）：是以优先于后代节点的顺序访问每个节点的。
     来看看它的代码实现实现如下：

  preOrderTraverse(callback) {
    this.preOrderTraverseNode(this.root, callback);
  }

  preOrderTraverseNode(node, callback) {
    if (node != null) {
      callback(node.key); //{1}
      this.preOrderTraverseNode(node.left, callback); //{2}
      this.preOrderTraverseNode(node.right, callback); //{3}
    }
  }

     先序遍历会先访问节点本身（{1}），然后再访问它的左侧子节点（{2}），最后是右侧子节点（{3}）
     通俗地说：也就是先打印自己（打印在这是指你要执行的回调函数，一般都是采取打印输出），再遍历完其左侧所有子节点，再遍历其右侧所有子节点
     我们先定义一个回调函数如下：

const printNode = (value) => console.log(value)

     然后执行前序遍历函数

tree.preOrderTraverse(printNode)

     观察控制台的输出

     为什么会是如此输出呢？如果你一下子没看明白，你可以看看我下面列出来的这段“代码”的执行过程（要注意结合注释来看哦）

tree.preOrderTraverse(printNode)->

preOrderTraverseNode(8,printNode)->         //直接执行{1}回调打印输出8
callback(8)
preOrderTraverseNode(8.left,printNode)=     //递归执行8.left其实就是传入2
preOrderTraverseNode(2,printNode)->         //直接执行{1}回调打印输出2
callback(2)
preOrderTraverseNode(2.left,printNode)->    //递归执行2.left，但是2的左边是null，所以就返回了，2的左边遍历完成，开始遍历右边
preOrderTraverseNode(2.right,printNode)=    //递归执行2.right其实就是传入3
preOrderTraverseNode(3,printNode)->         //直接执行{1}回调打印输出3
callback(3)
preOrderTraverseNode(3.left,printNode)->    //递归执行3.left，但是3的左边是null，所以就返回了，3的左边遍历完成，开始遍历右边
preOrderTraverseNode(3.right,printNode)->   //递归执行3.right，但是3的右边也是null，也是一样的返回，至此，8的左边已经全部遍历完成，所以开始遍历右边
preOrderTraverseNode(8.right,printNode)=    //递归执行8.right其实就是传入9
preOrderTraverseNode(9,printNode)->         //直接执行{1}回调打印输出9
callback(9)
preOrderTraverseNode(9.left,printNode)->    //递归执行9.left，但是9的左边是null，所以就返回了，2的左边遍历完成，开始遍历右边
preOrderTraverseNode(9.right,printNode)->   //递归执行9.right，但是9的右边也是null，所以就返回了，至此，整棵树遍历完成，然后函数结束

     执行该函数，首先传入根节点8，直接就会调用回调打印输出8，然后开始遍历8的左边，先是传入2，直接调用回调打印输出2，然后遍历2的左边，但是2的左边没有子节点返回，开始遍历2的右边，传入3，直接回调打印输出3，遍历3的左右两边都没有子节点，因为左子树已经全部遍历完成，直接返回到8，开始遍历8的右边，传入9，直接调用打印输出9，然后遍历9的左右两边都没有子节点，然后右子树也遍历完成，左右子树都已遍历完成，函数结束
     前序遍历就是只要传入该节点，就直接调用回调打印输出该节点，再开始遍历节点的左右两边。看完上述2个过程，相信你已经能理解二叉树的前序遍历了吧。

②中序遍历

     中序遍历：是一种以上行顺序访问二叉树所有节点的遍历方式，也就是以从最小到最大的顺序访问所有节点。
     其代码实现实现如下：

  inOrderTraverse(callback) {
    this.inOrderTraverseNode(this.root, callback);
  }

  inOrderTraverseNode(node, callback) {
    if (node != null) {
      this.inOrderTraverseNode(node.left, callback); //{1}
      callback(node.key); //{2}
      this.inOrderTraverseNode(node.right, callback); //{3}
    }
  }

     中序遍历会先访问其左侧子节点{1}，再调用回调输出打印自身{2}，最后才访问其右侧子节点{3}。
     也是一样的，通俗地说，中序遍历就是先递归遍历完左边所有节点，再打印输出自己，最后再遍历完右边所有节点
     回调函数不变：

const printNode = (value) => console.log(value)

     调用该中序遍历函数

tree.inOrderTraverse(printNode)

     观察控制台的输出

     可以看到，正如前面说的，是从小到大的顺序访问顺序，所以用二叉树做排序也是可以的，只不过一般很少这么做。
     还是一样的，你可以通过我下面列出来的这段“代码”来理解中序遍历的执行过程：

tree.inOrderTraverse(printNode)->

inOrderTraverseNode(8,printNode)->        //先遍历8的左边
inOrderTraverseNode(8.left,printNode)=  
inOrderTraverseNode(2,printNode)->        //先遍历2的左边
inOrderTraverseNode(2.left,printNode)->   //2的左边是null，所以就返回了
callback(2)                               //2的左边遍历完成，执行回调打印输出2，然后遍历右边
inOrderTraverseNode(2.right,printNode)=   //2的右子节点也就是传入3 
inOrderTraverseNode(3,printNode)->        //一样地先遍历3的左边
inOrderTraverseNode(3.left,printNode)->   //3的左边null，返回
callback(3)                               //3的左边遍历完成，执行回调打印输出3，然后遍历右边
inOrderTraverseNode(3.right,printNode)->  //3的右边null，返回到8
callback(8)                               //到这，8的左边已经全部遍历完成，所以执行{2}的回调打印输出8
inOrderTraverseNode(8.right,printNode)=   //遍历8的右边，传入9
inOrderTraverseNode(9,printNode)->        //先遍历9的左边
inOrderTraverseNode(9.left,printNode)->   //9的左边null，返回
callback(9)                               //9的左边遍历完成，执行回调打印输出9，然后遍历右边
inOrderTraverseNode(9.right,printNode)->  //9的右边null，返回。8的右边也遍历完成，整棵二叉树全部遍历完成，函数结束

     执行该函数，首先传入根节点8，会先遍历8的左边，于是传入2，传入2之后又会先遍历2的左边，2的左边为null返回，2的左边遍历完成，那么执行回调打印输出2，然后遍历2的右边，2的右边为3，传入3，传入3开始遍历3的左边，左边为null返回，3的左边遍历完成，那么就会回调打印输出3，然后遍历3的右边，右边为null返回，至此，8的左边子树已经全部遍历完成，回调打印输出8，开始遍历8的右边，8的右节点为9.传入9，然后开始遍历9的左边，左边为null返回，9左边遍历完成，回调打印输出9，开始遍历9的右边，右节点为null，返回，8的左右两边都已遍历完成，函数结束。
     中序遍历只要节点的左边遍历完成，那么就可以直接调用回调打印输出该节点了。

③后序遍历

     后序遍历：是先访问节点的后代节点，再访问节点本身。看其代码实现如下：

  postOrderTraverse(callback) {
    this.postOrderTraverseNode(this.root, callback);
  }

  postOrderTraverseNode(node, callback) {
    if (node != null) {
      this.postOrderTraverseNode(node.left, callback);  //{1}
      this.postOrderTraverseNode(node.right, callback);  //{2}
      callback(node.key);  //{3}
    }
  }

     后序遍历会先访问左侧子节点{1}，然后是右侧子节点{2}，最后是父节点本身{3}
     通俗地说，后序遍历会先遍历完左边所有节点，再遍历完右边所有节点，最后再回调打印输出自己本身。
     回调函数如下不变：

const printNode = (value) => console.log(value)

     调用该后序遍历函数

tree.postOrderTraverse(printNode)

     观察控制台的输出

     一样的，你可以先通过我下面列出来的这段“代码”来理解后序遍历的执行过程：

tree.postOrderTraverse(printNode)->

postOrderTraverseNode(8,printNode)->         //先遍历8的左边
postOrderTraverseNode(8.left,printNode)=
postOrderTraverseNode(2,printNode)->         //8的左节点即2，然后先遍历2的左节点
postOrderTraverseNode(2.left,printNode)->    //2的左节点为null，返回
postOrderTraverseNode(2.right,printNode)=    //2的右节点为3，传入3
postOrderTraverseNode(3,printNode)->         //先遍历3的左边
postOrderTraverseNode(3.left,printNode)->    //3的左边为null，返回
postOrderTraverseNode(3.right,printNode)->   //3的右边也为null
callback(3)                                  //3的左右两边遍历完成，调用回调打印输出3，然后返回
callback(2)                                  //返回到2，2的左右两边也遍历完成，调用回调打印输出2，然后返回
postOrderTraverseNode(8.right,printNode)=    //回到8，8的左边遍历完成，开始遍历8的右边
postOrderTraverseNode(9,printNode)->         //8的右节点为9，传入9，先遍历9的左边
postOrderTraverseNode(9.left,printNode)->    //9的左边为null，返回
postOrderTraverseNode(9.right,printNode)->   //9的右边也为null，返回
callback(9)                                  //9的左右两边遍历完成，调用回调打印输出9，然后返回
callback(8)                                  //返回到8，此时8的左右两边均已遍历完成，调用回调打印输出8，函数结束

     执行该函数，首先传入根节点8，然后开始遍历8的左边，传入8的左节点即2，开始遍历2的左边，2的左边为null，返回遍历2的右边，2的右节点为3，然后开始遍历3的左边，3的左节点为null返回，3的右节点也为null也返回，所以3的左右两边遍历完成，开始调用回调打印输出3，然后返回2，到这，2的左右两边也遍历完成了，所以调用回调打印输出2，再返回到8，8的左边已经全部遍历完成，开始遍历8的右边，传入8的右节点9，开始遍历9的左边，为null返回，再遍历9的右边，为null也返回，9的左右两边遍历完成，调用回调打印输出9，再返回到8，至此，8的左右两边已经全部遍历完成，调用回调打印输出8，整棵二叉树遍历完成，函数结束。
     能看到，后序遍历其实就是只要节点的左右两边遍历完成，那么就可以调用回调打印输出该节点了。

④小结

     不管前序、中序还是后序遍历，并不需要死记硬背，只要掌握其回调函数在遍历左右的前面、中间还是后面，那么就能够知道是什么遍历顺序了，根据函数的执行顺序来进行理解，你就能够理解这三种遍历方式。其次我们要理解，这三种遍历都用到了递归，它用到的是递归栈，执行的函数从栈顶到栈底一层一层函数执行了就往回返回,直到整个栈为空。

⑤二叉树面试例题

     讲一道题目，是一个后端朋友最近面试题中的二叉树相关的题
题干：我们用兴盛优选研发团队的岗位做了一棵二叉树，这棵二叉树的中序遍历序列为：后端——UI——产品经理——测试——项目经理——运维——前端——DBA；后序遍历序列为：UI——后端——测试——产品经理——运维——DBA——前端——项目经理。
问题1：请画出这棵二叉树的形状，并且写出你的推导过程。
问题2：请写出这棵二叉树的前序遍历序列。
     先分析一下题目，这道题主要是要把问题1解出来，那么问题2就很简单了，能把整棵二叉树推导出来的话，写个前序遍历那不是简简单单。所以我们得先根据给出的两个遍历序列推导出这一棵二叉树。
  中序：后端——UI——产品经理——测试——项目经理——运维——前端——DBA
  后序：UI——后端——测试——产品经理——运维——DBA——前端——项目经理
     后序遍历有什么特点呢？先将左右两边都遍历完成，再打印输出自己本身，那么想一下根节点是不是永远最后才输出，因为根节点左右两边的子树不遍历完成，轮不到他打印输出自己的，所以这是关键点，那么我们就能够确定项目经理肯定是根节点。
     中序遍历的特点是左边遍历完成，就打印输出自己。而项目经理又是根节点，所以在项目经理左边的后、U、产、测都是构成项目经理的左子树节点，而在项目经理右边的运、前、D都是构成项目经理右子树节点。如下图所示：

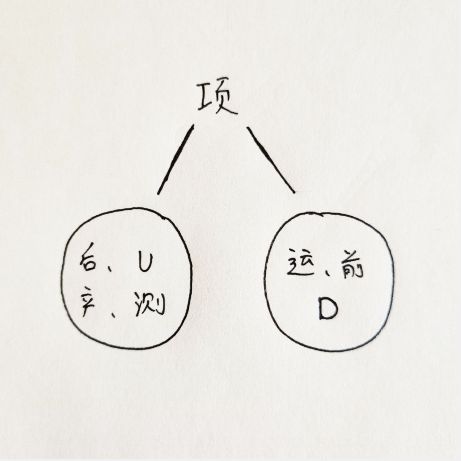
     确定这个结构之后，我们先处理一下左子树的具体结构，左子树的中序遍历：后端——UI——产品经理——测试；左子树的后序遍历：UI——后端——测试——产品经理，还是一样的能够确定产品经理是左子树的根节点，因为他在后序遍历的最后，然后看中序遍历顺序，后端跟UI在产品经理的左边，构成了产品经理的左子树，右边只有测试一个节点，所以测试肯定就直接是产品经理的右节点了。如此一来便像下图一样：

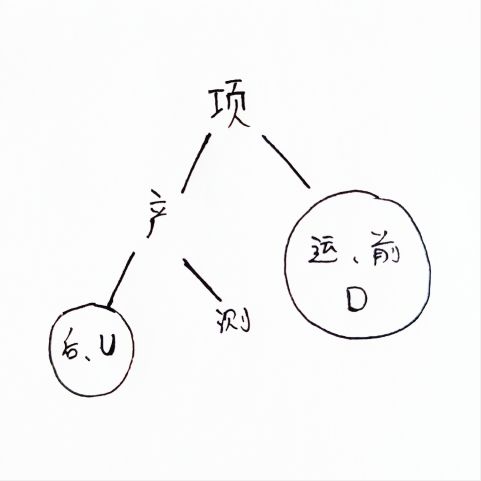
     还是一样地确定后、U这两个节点，左子树的中序遍历：后端——UI，左子树的后序遍历：UI——后端，所以后端是这边的根节点，有下面两种情况

          图1×（不符合中序遍历）

          图2√（符合）
     图1的中序遍历是U-后-产-测跟给定的中序遍历顺序不符，所以应该是图2的结构是正确的。最后还有右子树很容易确定，因为右子树的后序遍历顺序为运维——DBA——前端，所以前端是右子树的根节点，再根据右子树的中序遍历顺序为运维——前端——DBA，那么就能够确定，运维在前端左边构成左节点，DBA在前端右边构成右节点。所以最后确定整棵二叉树的结构如下图：

     问题1解决了，那么问题2也就很容易了，前序遍历顺序为：项目经理——产品经理——后端——UI——测试——前端——运维——DBA。希望看完之后，你能够记住前序、中序、后序三者的区别，以后看到这种题目，我们只需要根据他们遍历的一些特点来找到突破口切入便可以很快解决这类问题。

     后面这些知识点陆续有空会发布新文章更新，文中如果哪里写的不对的，还请大家指出，谢谢。