3000字入门图神经网络
0x01 Intro
图:就是图论里那个图啦
神经网络:联结主义。
图神经网络:在图上搞联结主义。
那么问题就来了,包括但不限于,怎么表示图、怎么在图上搞联结。
0x02 图的表示
首先,什么是图?
图是表示节点(点)和节点间关系(边)的数据结构。
也可以给图定义一个全局的信息,比如节点数量、最长路径长度等等。
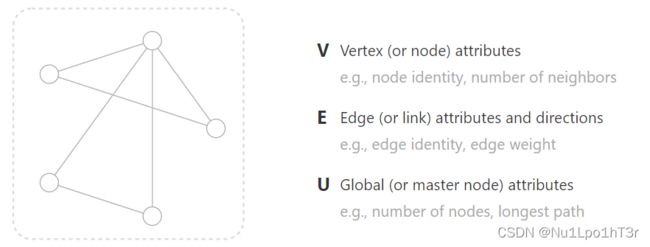
我们可以给图上的节点、边、全局信息做一些嵌入,具体地来说,就是用向量来表示它们带有的信息。比如下图中,节点用六维向量、边用八维向量、全局信息用五维向量表示。
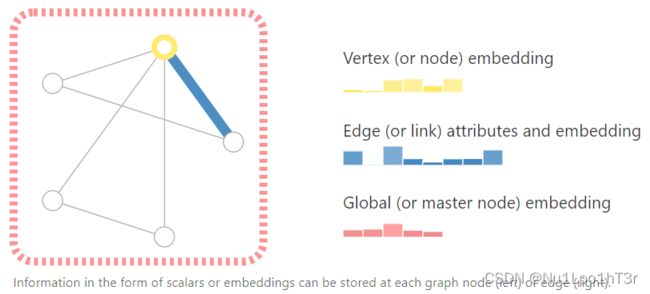
目前为止,我们只是存储了每个元素之间的关系。我们还需要记录和表示更多的关系,比如节点的连结(边),边的方向性 etc。
0x03 图的场景
目前觉得,万物皆可表示成图。
0x04 图的任务
总地来说,咱们手里已有数据(图和它上面记录的信息),需要完成一些任务。主要有这么几类。
- 节点分类(对单个节点做分类,如某个网络节点是不是DDOS肉鸡)
- 图分类(对整个图做分类,如分子有毒无毒)
- 节点聚类(把DDOS肉鸡聚在一块)
- 链接预测(我和我初中同学的发小的补习班同学的npy可不可能认识)
- 影响最大化(如何在人群之中一眼认出自己的对象)
0x05 图机器学习的挑战
现在图已经有了,如何在上面搞联结主义呢?第一步是考虑我们怎么把图和神经网络结合。
机器学习模型通常用张量作为输入,但图的结构就多了去了。 因此,如何以与深度学习兼容的格式来表示图是值得思考的。 图有四种类型的信息,我们会使用这些信息进行预测:节点信息、边信息、全局上下文信息和连接性。
前三个是相对简单的:都是向量,存就得了呗。
但是,表示图的连通性要复杂得多。直观的想法是用邻接矩阵(如下图)。但是,图一旦大了之后,存储空间就跟着大了(邻接矩阵是n*n的),而且大部分的图都是稀疏的,意味着邻接矩阵的大部分元素都是0。
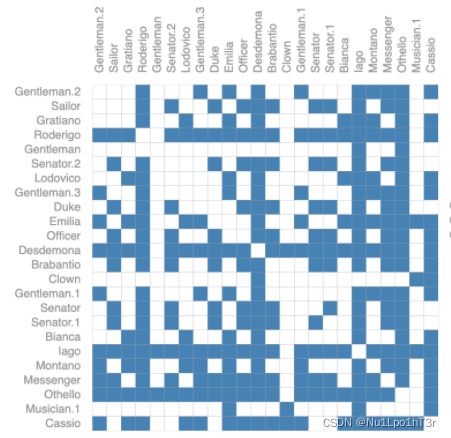
此外,下面两个邻接矩阵表示的其实是同一个图。这里,矩阵每行/每列表示一个节点。可以发现,我们把行列调一个个,邻接矩阵就不一样了,而这可能就意味着不同的结果。因此,我们用来记载图结构的方法需要确保图结构的置换不变性。

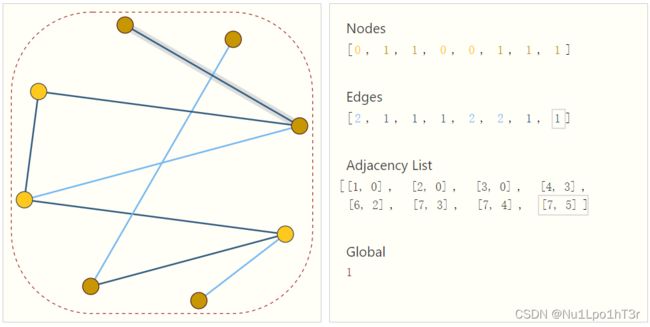
一种优雅的方法是储存每一条(真实存在的)边,可以理解为邻接矩阵里表示的非0边。比如下图:节点数是固定的(节点的值可能是0或1),记录了每条边的信息(1或者2),记录了每条边连的是哪两个节点,也记录了全局信息。
0x06 图神经网络
目前图神经网络的主流是消息传递图神经网络(首发于文章Neural Message Passing for Quantum Chemistry)。
GNN采用“图形输入,图形输出”的架构,这意味着GNN接受图作为输入,将信息(前文说的向量)加载到其节点、边缘和全局上下文中,并逐步调整这些信息,但是不改变输入图的连接性。
接下来我们会从易到难,看看怎么搭一个图神经网络。
最简单的版本
这版GNN 在图的每个组件(节点、边、全局信息)上分别使用普通的神经网络;我们称之为 GNN 层。 对于每个节点向量,我们把它扔到节点向量的网络中并输出一个新的节点向量。我们对每条边和全局上下文做同样的事情。
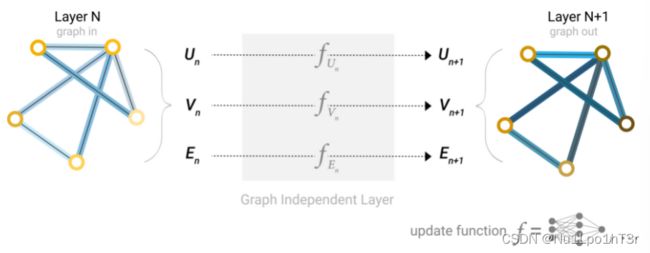
于是,我们可以把这些GNN层摞起来搞成深度图神经网络。
因为 GNN 不会更新输入图的连通性,所以我们可以用与输入图相同的邻接表和相同数量的特征向量来描述 GNN 的输出图。 但是,输出图更新了映射成信息的向量,因为 GNN 更新了每个节点、边和全局上下文表示。
通过池化做GNN预测
如何用上面说的图神经网络做预测呢?
假设任务是对节点做二分类预测/多分类预测/回归:好办,直接把节点信息的向量扔到一个神经网络里。
但是也没这么好办。因为,很多信息,比如边和全局的信息都没用上,或者说节点根本就没有信息,信息全在边里。于是,应该从边中提取信息。
可以用池化的方法来从边中拿信息。
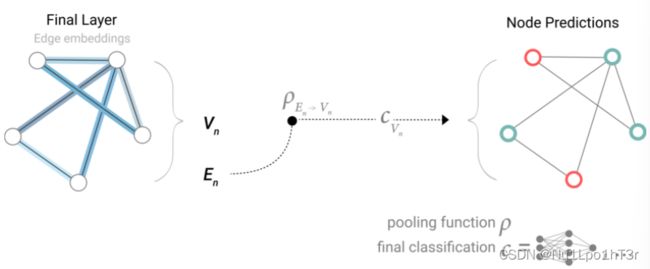
池化的原理如下图,我们有边上的信息和全局的信息,想生成节点的信息,就可以把节点接出来的所有边的向量都拿过来,做一下向量的求和。
于是我们这个节点二分类(多分类/回归)任务可以如下图这么做:先池化再扔进神经网络。
同理,边的信息或者全局的信息也可以用这样的池化-网络方法得到。
这里要注意一件事,比如咱们在用边的信息预测点,这里根本没有在GNN层里体现图的连通性,每一个节点都只是看了他相邻的边,因此每一个节点都可以独立地做预测/分类的事情(意味着并行化的可能)。我们只在汇集信息做预测的时候使用连通性。
在图的各个部分之间传递信息
说到传递信息,我想到一个计算机网络里的例子。
在Internet中有若干路由器。它们构成了一个十分复杂的网络。对于一个指定了终点的数据包,每个路由器会根据这个终点的网段决定把这个包发到哪个路由器上。而路由器的转发策略是基于其他路由器的局部信息的聚合生成的。通过策略迭代,每个路由器隐式地了解了远端路由器的信息,或者说每个路由器都知道了全图的结构。
我们可以通过在 GNN 层中使用池化来进行更复杂的预测,以使每个节点/边/全局学到图的连通性。 消息传递(message passing)可以确保这一点,其中相邻节点或边缘交换信息并影响彼此更新的嵌入。
以节点的消息传递为例,主要分为三个步骤:
- 对于图上的每个节点,收集所有相邻节点的嵌入或者消息。
- 通过聚合函数(如 sum)聚合所有消息。
- 所有汇集的消息都通过一个更新函数传递,通常是一个神经网络。
概括一下就是收集信息,聚合,扔进网络。
如下图所示,我们要在实心点上写入相邻节点的信息。这就需要我们收集它所有相邻节点的信息并且求和,然后扔到一个神经网络里面,生成新的(聚合过的)信息。
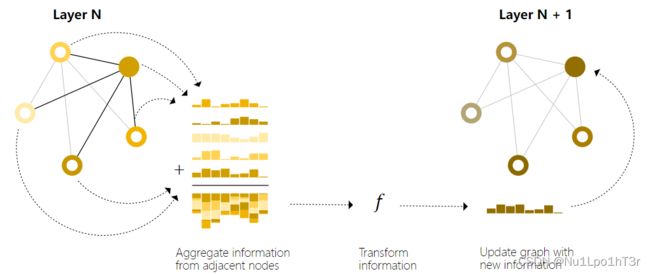
当然,上面的消息传递只是最简单的一种。
上述的操作和图像中的标准卷积池化操作十分相似。其本质区别在于,图的相邻节点是可变的。
下图是 GCN 架构的示意图,它通过在每个节点收集距离为 1 度的相邻节点的信息来更新图的节点信息。
学习边的表示
数据集一般不会包含所有类型的信息(节点、边缘和全局上下文)。 前面讲了我们想对节点进行预测,但我们的数据集只有边缘信息的情形下,如何使用池化将信息从边缘路由到节点,但这仅限于模型的最后预测步骤。 我们可以使用消息传递在 GNN 层内的节点和边之间共享信息。
现在的问题是,如何在每一层都聚合相邻点边的信息呢?
一个问题是,点和边的向量维度可能不一样,因此可能的想法是搞一个线性映射,或者是在扔进神经网络之前,把点和边的信息都拼到一块去。
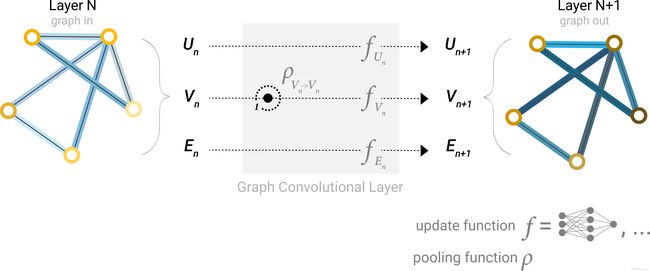
如下图,在每一层GNN层中,更新哪些图属性和以什么顺序更新都是可以自己指定的。
加入全局信息
目前为止,我们描述的GNN还有一个缺陷:即使有很多次消息传递,图中彼此相距很远的节点也可能无法有效地相互传递信息。原因很简单,对于一个节点,如果我们有 k 层,则信息将最多传播 k 步。
如果节点相距很远的话,这就不好玩了。一种解决方案是让所有节点能够相互传递信息。但是对于很大的图,这件事成本很高(尽管这种称为“虚拟边”的方法已用于诸如分子之类的小型图)。
一种解决方法是使用图的全局信息,它有时被称为主节点或上下文。 这个全局向量连接到网络中的所有其他节点和边,并且可以充当它们之间的桥梁以传递信息,从而为整个图建立表示。 这创建了一个比其他方式学习的更丰富、更复杂的图表示。
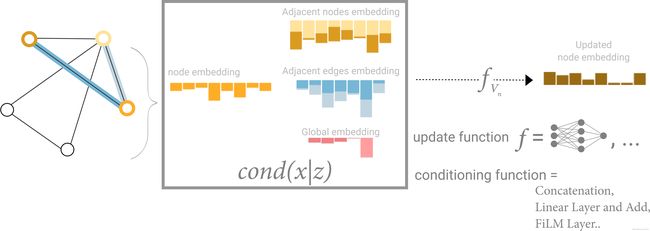
这里,所有图属性都做了学习,我们可以在池化期间通过加入我们感兴趣的属性信息来完成信息聚合。 例如,对于一个节点,我们可以考虑来自相邻节点、连接边和全局信息的信息。 为了使新节点嵌入所有这些可能的信息源,我们可以简单地将它们的向量拼到一块。 此外,我们还可以通过线性映射将它们映射到相同的空间并添加它们或应用特征调制层(参见文章Feature-wise transformations),方法很多。