【十二届蓝桥杯国赛真题】123 --- 时间复杂度O(1)的纯数学解法
文章目录
-
-
- 题目链接
- 解题思路
- AC代码
-
往期蓝桥杯真题解析
【蓝桥杯真题训练 day14】今日四道真题全解析
【蓝桥杯冲刺 day12】题目全解析
【蓝桥杯冲刺 day10】题目全解析 — 难题突破
【蓝桥杯冲刺 day8】题目全解析 —附上LeetCode 每日一题
【蓝桥杯冲刺 day7】 题目全解析 — 附上LeetCode周赛 银联-03. 理财产品
【蓝桥杯冲刺 day4】题目全解析 — 每日刷题解析
写在前面
Hello大家好我是秋刀鱼,今天又来给大家带来蓝桥杯真题题解了。
今天做的题中唯独这道题蛮有难度,前前后后花费了我将近一个半小时的时间才彻底悟透。我看了很多大佬的题解都是使用二分的方法来做,但在这里我给大家带来一个数学解法,时间、空间复杂度 O ( 1 ) O(1) O(1)。
因为本题较难所以本篇幅较长,希望你能耐心看完。
题目链接
小蓝发现了一个有趣的数列,这个数列的前几项如下:
1, 1, 2, 1, 2, 3, 1, 2, 3, 4, …
小蓝发现,这个数列前 1 项是整数 1,接下来 2 项是整数 1 至 2,接下来3 项是整数 1 至 3,接下来 4 项是整数 1 至 4,依次类推。
小蓝想知道,这个数列中,连续一段的和是多少?输入格式
输入的第一行包含一个整数 T,表示询问的个数。
接下来 T 行,每行包含一组询问,其中第 i 行包含两个整数 li 和 ri,表示询问数列中第 li 个数到第 ri 个数的和。
输出格式
输出 T 行,每行包含一个整数表示对应询问的答案。
样例输入
3
1 1
1 3
5 8
样例输出
1
4
8评测用例规模与约定
对于 10% 的评测用例, 1 ≤ T ≤ 30, 1 ≤ li ≤ ri ≤ 100。
对于 20% 的评测用例, 1 ≤ T ≤ 100, 1 ≤ li ≤ ri ≤ 1000。
对于 40% 的评测用例, 1 ≤ T ≤ 1000, 1 ≤ li ≤ ri ≤ 10 ^ 6。
对于 70% 的评测用例, 1 ≤ T ≤ 10000, 1 ≤ li ≤ ri ≤ 10 ^ 9。
对于 80% 的评测用例, 1 ≤ T ≤ 1000, 1 ≤ li ≤ ri ≤ 10 ^ 12。
对于 90% 的评测用例, 1 ≤ T ≤ 10000, 1 ≤ li ≤ ri ≤ 10 ^ 12。
对于所有评测用例, 1 ≤ T ≤ 100000, 1 ≤ li ≤ ri ≤ 10 ^ 12。
解题思路
开始之前需要了解的数学公式:
- 等差数列求和公式: S = ( a 1 + a n ) ∗ n / 2 S=(a_1+a_n)*n/2 S=(a1+an)∗n/2 ,其中 a 1 a_1 a1 为等差数列首项, a n a_n an 为等差数列末尾项, n n n 为求和项数量。
- 从1开始的平方求和公式 ∑ 1 n i 2 = n ∗ ( n + 1 ) ∗ ( 2 ∗ n + 1 ) / 6 \sum_1^n i^2 = n*(n+1)*(2*n+1)/6 ∑1ni2=n∗(n+1)∗(2∗n+1)/6
现在开始我们的思路:
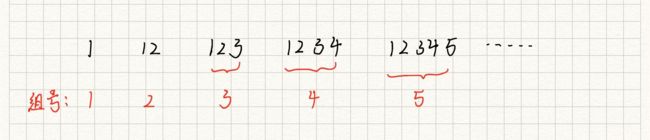
我把连续递增的一串数字定义为一组,按照依次的顺序为组附上编号,编号从1开始。例如:
题目中会给定第 l , r l,r l,r个数字,可以通过一定的方法分别获得 l , r l,r l,r 所对应的组与组中具体的位置。那么如何确定任意一个数字的组号与组内位置呢?如果能够获得具体位置,就能够根据组的位置获得组之间数字数量,因此这是解题的关键。
不难发现,第 i i i 组所拥有的数字个数为 i i i ,每一组提供的数字数量比上一组数量多一个,所以是一个等差数列。因此数字 l , r l,r l,r对应的组能够通过等差数列求和公式得到。假设所在的组为 n n n,根据公式: n ∗ ( n + 1 ) / 2 = l n*(n+1)/2 = l n∗(n+1)/2=l 获得 n 的值,但是这样求得组号是从0开始的,因此还需要加一才能获得真正的组号group。
既然获得了组,再根据等差数列求和公式就能获得其在组中的位置number,下面是具体实现的代码:
#define pii pair
...
// 返回组号与组中位置
pii get(ll pos) {
double tmp = sqrt(pos * 2) - 0.5;
ll group = (ll)tmp + 1;
ll number = pos - (group * (group - 1)) / 2;
return { group,number };
}
现在获得了两个 (组,编号) 位置,那么我们怎么获得组与组之间,有多少个数字呢?先看看下面这张图:

定义如图中所示。
为了获得 [ l , r ] [l,r] [l,r] 数字之和,我们可以将问题简化为求:红方框中数字总和 - l l l 本组的左侧数字总和(蓝色部分) + r r r 本组的左侧数字总和(黄色部分)。
对于后面两个"左侧数字总和"很容易就能得出,因为每一组的值都是一个从1开始的单调递增数列,使用数列的求和公式能够快速得到。定义数列求和函数:
// 等差数列求和
// a1: 第一项的值
// an: 第n项的值
// n: 求和项的个数
ll sum(ll a1, ll an, ll n) {
return n * (a1 + an) / 2;
}
定义第 i i i 组数的数字总和为 s u m i sum_i sumi ,那么现在问题转换为:求 s u m g 1 + s u m g 1 + 1 + . . . . + s u m g 2 − 1 sum_{g1}+sum_{g1+1}+....+sum_{g2-1} sumg1+sumg1+1+....+sumg2−1 的值,换句话说就是求:编号范围 [ g 1 , g 2 − 1 ] [g_1,g_2-1] [g1,g2−1] 组所有数字之和。
那么我们假设 g 1 g_1 g1 组的数字和为 A A A,假设 g 1 g_1 g1组最后一个数字为B ,那么就有如下:
为了获取以上所有数的值,我们可以使用分割的思想,先单纯计算图中 A、B 的值。
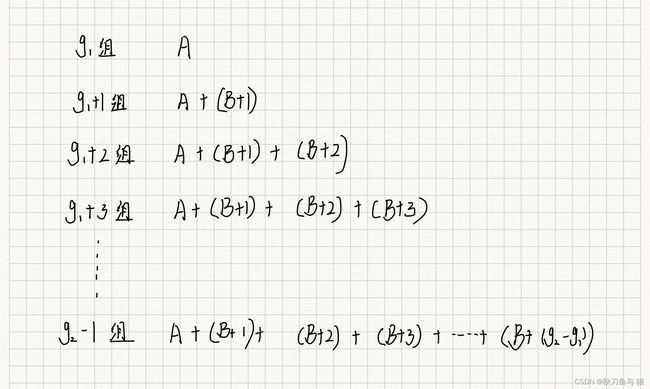
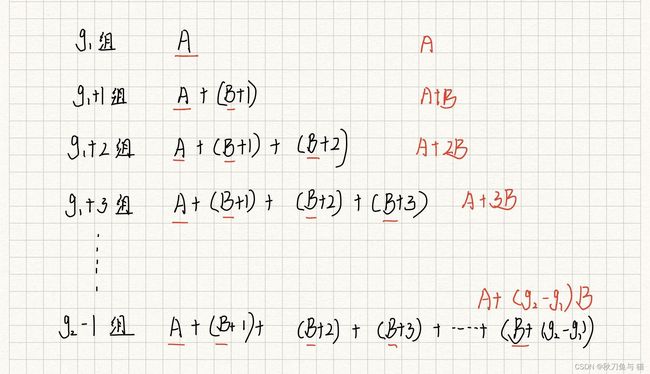
定义 g 2 − g 1 g_2-g_1 g2−g1 的值为 n n n, n − 1 n-1 n−1 的值为 m 。
可以看到:A与B 的分布是一个等差数列,首项是 A A A ,末尾项是 A + ( N ∗ B ) A+(N*B) A+(N∗B) ,求和项的个数为 N + 1 N+1 N+1 ,因此我们能够通过等差数列求和公式先计算出所有 A 、 B A、B A、B 的值。计算完 A 、 B A、B A、B 的值之后继续计算剩余值:

最终通过等差数列求和与平方和公式得到剩下的值。
AC代码
#include
#define ll long long
using namespace std;
// 等差数列求和
ll sum(ll a1, ll an, ll n) {
return n * (a1 + an) / 2;
}
// 求和
ll getGap(ll l, ll r) {
ll ret = 0;
ll n = r - l;
ll m = n - 1;
ll a1 = sum(1, l, l);
ll an = a1 + m * l;
// 单纯计算A的总值
ret += sum(a1, an, n);
// 需要计算剩余值,使用平方和公式与等差数列求和
if (n >= 2) {
ret += sum(1, m, m) * (m + 1) - m * (m + 1) * (2 * m + 1) / 6;
}
return ret;
}
// 获取组号与具体位置
pii get(ll pos) {
double tmp = sqrt(pos * 2) - 0.5;
ll group = (ll)tmp + 1;
ll number = pos - (group * (group - 1)) / 2;
return { group,number };
}
int main()
{
ll n;
cin.tie();
cin >> n;
while (n--) {
ll l, r;
cin >> l >> r;
pii left = get(l);
pii right = get(r);
cout << getGap(left.first, right.first) + sum(1,right.second,right.second) - sum(1,left.second-1,left.second - 1) << endl;
}
return 0;
}
写在最后
代码、论述中有任何问题,欢迎大家指出,同时如果有任何疑问,也能够在评论区中留言,大家共同讨论共同进步!
如果觉得博主写的不错的话,可以点赞支持一下!ღ( ´・ᴗ・` )比心