【蓝桥python冲刺31天】——如何轻松拿捏必考数论题?(第一弹)
 大家好,我是每天刷题的小蓝,欢迎交流指正~
大家好,我是每天刷题的小蓝,欢迎交流指正~ 
目录
真题Ⅰ:年龄巧合
题目
题解
代码
真题Ⅱ:纸牌三角形
题目
题解
代码
真题Ⅲ:取球游戏
题目
题解
代码
真题Ⅰ:年龄巧合
题目
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小明和他的表弟一起去看电影,有人问他们的年龄。小明说:今年是我们的幸运年啊。我出生年份的四位数字加起来刚好是我的年龄。表弟的也是如此。已知今年是 20142014 年,并且,小明说的年龄指的是周岁。
请推断并填写出小明的出生年份。
题解
难度系数:⭐
考察题型:填空题, 2014, 国赛
涉及知识点:数论-方程
「小蓝思路」
一、小蓝拿到题目的第一步,就是从题目中定位关键句:
“我出生年份的四位数字加起来刚好是我的年龄”。
可以看出里面正好是两个等式,构成一个方程:我的年龄=出生年份的四位数字加起来
2014-x==int(str(x)[0])+int(str(x)[1])+int(str(x)[2])+int(str(x)[3])前者我的年龄:现在的2014年-出生日期(2014-x)
后者出生年份相加:先用字符串切片然后相加(1+9+8+8)
二、题目中又提到:“表弟的也是如此”。说明这种幸运年有两个,分别是1988和2006
按照常识:表哥年龄比表弟年龄大,所以最后只需打印表哥的1988ヾ(≧▽≦*)o
代码
#数论方程-年龄巧合
for x in range(1000,2014):#遍历查找出生日期
if 2014-x==int(str(x)[0])+int(str(x)[1])+int(str(x)[2])+int(str(x)[3]):
print(x)#表哥:1988 表弟:2006
break #输出表哥的出生日期就停止遍历真题Ⅱ:纸牌三角形
题目
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
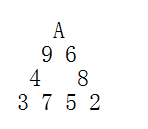
A,2,3,4,5,6,7,8,9 共 9 张纸牌排成一个正三角形(A 按 1 计算)。要求每个边的和相等。
下图就是一种排法。
这样的排法可能会有很多。
如果考虑旋转、镜像后相同的算同一种,一共有多少种不同的排法呢?
请你计算并提交该数字。
题解
难度系数:⭐⭐
考察题型:填空题, 2017, 省赛
涉及知识点:数论-全排列
「小蓝思路」
一、题目中说:“A,2,3,4,5,6,7,8,9 共 9 张纸牌排成一个正三角形(A 按 1 计算)。”
9张纸牌,就是9个坑,用不同的数字填它就完了~
关键是如何才能轻松枚举所有情况呢?
最简单的方法:调用强大的工具库(itertools)的全排列函数(permutations)。
二、看到题干的关键句:“如果考虑旋转、镜像后相同的算同一种”。
因为3种旋转*嵌套的2种镜像=6种情况,所以最后总数要除以6种重复情况(´▽`ʃ♡ƪ)
代码
#数论全排列-纸牌三角形
from itertools import permutations #导入全排列函数
cnt=0 #排法初始化为0
for i in permutations(range(1,10)): #i=(1, 2, 3, 4, 5, 6, 7, 8, 9)
a=i[0]+i[1]+i[2]+i[3]
b=i[0]+i[4]+i[5]+i[6]
c=i[3]+i[6]+i[7]+i[8]
if a==b==c: #abc三边和相等
cnt+=1 #排法+1
print(cnt//6) #144种排法 真题Ⅲ:取球游戏
题目
今盒子里有 n 个小球,A、B 两人轮流从盒中取球,每个人都可以看到另一个人取了多少个,也可以看到盒中还剩下多少个,并且两人都很聪明,不会做出错误的判断。
我们约定:
每个人从盒子中取出的球的数目必须是:1,3,7 或者 8 个。轮到某一方取球时不能弃权!
A 先取球,然后双方交替取球,直到取完。被迫拿到最后一个球的一方为负方(输方)
请编程确定出在双方都不判断失误的情况下,
输入描述
先是一个整数 n(n<100),表示接下来有 n 个整数。
然后是 n 个整数,每个占一行(整数< 10^4),表示初始球数。
输出描述
程序则输出 n 行,表示 A 的输赢情况(输为 0,赢为 1)。
样例输入
4
1
2
10
18样例输出
0
1
1
0题解
难度系数:⭐⭐⭐
考察题型:博弈论, 2012, 省赛
涉及知识点:数论-博弈论
「小蓝思路」
一、题目中说:“对于特定的初始球数,A 是否能赢?”。
一开始先让A全输(初始化dp列表为0)
接下来只需要统计A必赢的情况(把0改成1)
二、题目中解释:“A 先取球,然后双方交替取球,直到取完。被迫拿到最后一个球的一方为负方(输方)”。
先思考一下A什么情况必赢?条件是什么?
当最后一轮A先取球,B只能取一个球时,那么A必赢。
三、题目中指出:“每个人从盒子中取出的球的数目必须是:1,3,7 或者 8 个”。
那么当遇到必输情况时(dp[i]==0)
加上1,3,7,8就转化成必赢情况(dp[i+1]=dp[i+3]=dp[i+7]=dp[i+8]=1)
举个栗子
假如一共1个球,A先取1个球,A输。
假如一共2个球,A先取1个球,B取最后1球,A赢。
假如一共3个球,A先取1个球,B取1个球,A取最后1球,A输。
假如一共4个球,A先取3个球,B取最后1球,A赢。
四、最后小Tips:“然后是 n 个整数,每个占一行(整数< 10^4),表示初始球数。”
因为样例输入n< 10**4,所以dp列表初始化最大为9999 q(≧▽≦q)
代码
#数论-取球游戏
dp=[0 for i in range(10000)] #初始化A全输
n=int(input())
for i in range(n):
x=int(input())
for i in range(1,x+1): #遍历所有情况
if dp[i]==0: #当A必输时
dp[i+1]=dp[i+3]=dp[i+7]=dp[i+8]=1 #下面情况A必赢
print(dp[x])
#样例输入1 2 10 18
#x = 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
#dp=[0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0]
 友友们,备战蓝桥最后29天,让我们撸起袖子加油干!
友友们,备战蓝桥最后29天,让我们撸起袖子加油干!
![]()