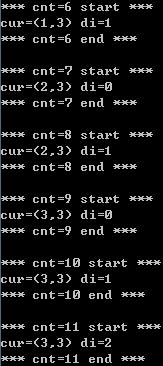
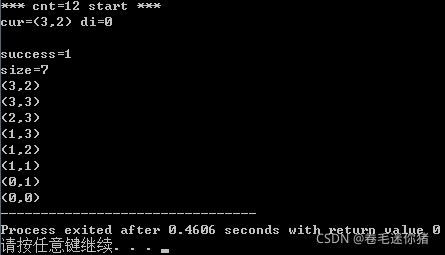
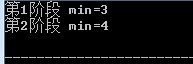
小肥柴慢慢手写数据结构(C篇)(3-2 Stack应用举例)
小肥柴慢慢手写数据结构(C篇)(3-2 Stack应用举例)
- 目录
-
- 3-6 括号匹配(平衡符号)
- 3-7 计算器
- 3-8 迷宫问题(其实可以不用栈)
- 3-9 最小栈(双栈的第一次使用)
- 3-10 单调栈(正向/反向栈)
目录
3-6 括号匹配(平衡符号)
在黑皮书P52中,这个问题被称为“平衡符号”,而在严版教材P49中设为3.2.2 括号匹配的检验,问题本质是一样的。
【问题描述】编译器会检查当前代码中括号是否都能成对出现,否则会造成编译问题,也就是说:“[()]”是合法的,而“[(])”是非法的。
【思考】这个问题明显可以用栈去解决:每次从被检测数组中取出一个元素,(1)如果是括号,则同栈顶元素比较,如果两个元素(都是括号)能匹配成功,则栈顶元素出栈;否则将新的括号元素压栈。(2)如果不是括号,不执行上述操作。
上代码:
1.使用的栈原型
(1)ArrayStack.h 我们选用基于动态数组的栈来实现括号匹配功能,其中ElementType变更为char型,对于String类型暂不考虑(如无必要勿添新知)
#ifndef _ARRAY_STACK_H
#define _ARRAY_STACK_H
#define EMPTY_TOS (-1)
#define DEFAULT_CAPACITY (20)
#define OK (0)
#define ERROR (-1)
typedef char ElementType;
struct StackRecord {
int capacity;
int topIndex;
ElementType *array;
};
typedef struct StackRecord *Stack;
int isEmpty(Stack S);
int isFull(Stack S);
Stack createStack();
void disposeStack(Stack S);
void makeEmpty(Stack S);
void push(ElementType X, Stack S);
ElementType top(Stack S);
void pop(Stack S);
ElementType topAndPop(Stack S);
void printStack(Stack S);
#endif
(2)ArrayStack.c 具体实现不变,对于空栈时的top等操作,设定特殊字符“*”
#include 2.核心代码
void checkMatch(char arr[], int len) {
int i;
printf("\n测试数据:");
for (i = 0; i < len; i++)
printf("%c ", arr[i]);
Stack stack = createStack();
for (i = 0; i < len; i++) {
char cur = top(stack);
if ((cur == '(' && arr[i] == ')')
|| (cur == '[' && arr[i] == ']')
|| (cur == '{' && arr[i] == '}'))
pop(stack);
else
push(arr[i], stack);
}
printf(" %s", isEmpty(stack) ? "匹配成功" : "匹配失败");
}
- 测试代码
#include 测试结果:

——————————
严版教材实现
1.c1.h 第一章的原始定义
// c1.h (程序名)
#include2.c3-1.h 栈的顺序存储表示
// c3-1.h 栈的顺序存储表示
#define STACK_INIT_SIZE 10 // 存储空间初始分配量
#define STACKINCREMENT 2 // 存储空间分配增量
struct SqStack
{
SElemType *base; // 在栈构造之前和销毁之后,base的值为NULL
SElemType *top; // 栈顶指针
int stacksize; // 当前已分配的存储空间,以元素为单位
}; // 顺序栈
3.bo3-1.cpp 顺序栈(存储结构由c3-1.h定义)的基本操作(9个)
// bo3-1.cpp 顺序栈(存储结构由c3-1.h定义)的基本操作(9个)
Status InitStack(SqStack &S)
{ // 构造一个空栈S
if(!(S.base=(SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType))))
exit(OVERFLOW); // 存储分配失败
S.top=S.base;
S.stacksize=STACK_INIT_SIZE;
return OK;
}
Status DestroyStack(SqStack &S)
{ // 销毁栈S,S不再存在
free(S.base);
S.base=NULL;
S.top=NULL;
S.stacksize=0;
return OK;
}
Status ClearStack(SqStack &S)
{ // 把S置为空栈
S.top=S.base;
return OK;
}
Status StackEmpty(SqStack S)
{ // 若栈S为空栈,则返回TRUE,否则返回FALSE
if(S.top==S.base)
return TRUE;
else
return FALSE;
}
int StackLength(SqStack S)
{ // 返回S的元素个数,即栈的长度
return S.top-S.base;
}
Status GetTop(SqStack S,SElemType &e)
{ // 若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR
if(S.top>S.base)
{
e=*(S.top-1);
return OK;
}
else
return ERROR;
}
Status Push(SqStack &S,SElemType e)
{ // 插入元素e为新的栈顶元素
if(S.top-S.base>=S.stacksize) // 栈满,追加存储空间
{
S.base=(SElemType *)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType));
if(!S.base)
exit(OVERFLOW); // 存储分配失败
S.top=S.base+S.stacksize;
S.stacksize+=STACKINCREMENT;
}
*(S.top)++=e;
return OK;
}
Status Pop(SqStack &S,SElemType &e)
{ // 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR
if(S.top==S.base)
return ERROR;
e=*--S.top;
return OK;
}
Status StackTraverse(SqStack S,Status(*visit)(SElemType))
{ // 从栈底到栈顶依次对栈中每个元素调用函数visit()。
// 一旦visit()失败,则操作失败
while(S.top>S.base)
visit(*S.base++);
printf("\n");
return OK;
}
4.algo3-3.cpp 解决问题的核心代码
// algo3-3.cpp 括号匹配的检验,(限于()、[])
typedef char SElemType;
#include"c1.h"
#include"c3-1.h"
#include"bo3-1.cpp"
void check() { // 对于输入的任意一个字符串,检验括号是否配对
SqStack s;
SElemType ch[80],*p,e;
if(InitStack(s)) {// 初始化栈成功
printf("请输入表达式\n");
gets(ch);
p=ch;
while(*p) // 没到串尾
switch(*p) {
case '(':
case '[':Push(s,*p++);
break; // 左括号入栈,且p++
case ')':
case ']':if(!StackEmpty(s)) {// 栈不空
Pop(s,e); // 弹出栈顶元素
if(*p==')'&&e!='('||*p==']'&&e!='[') { // 弹出的栈顶元素与*p不配对
printf("左右括号不配对\n");
exit(ERROR);
} else {
p++;
break; // 跳出switch语句
}
} else {// 栈空
printf("缺乏左括号\n");
exit(ERROR);
}
default: p++; // 其它字符不处理,指针向后移
}
if(StackEmpty(s)) // 字符串结束时栈空
printf("括号匹配\n");
else
printf("缺乏右括号\n");
}
}
void main() {
check();
}
对比起来还是设计思路上有表像的不同,尽量简单规范就行,因为代码不是拿来炫耀的,大多数人都是普通人,不要装神仙。我们可以参看labuladong的《算法小抄》中相关讨论(C++)(转载)
bool isValid(string str){
stack<char> left;
for(char c : str){
if (c == '(' || c == '{' || c == '['){
left.push(c);
} else {
if (!left.empty() && leftOf(c) == left.top())
left.pop();
else
return false;
}
}
return left.empty();
}
char leftOf(char c){
if (c == '}')
return '{';
if (c == ')')
return '(';
return '[';
}
3-7 计算器
注:参考《labuladong算法小抄》解读修改
很多讲解数据结构的教材/教程(例如严版教材算法3.3 P52),都喜欢用双栈来解决计算器问题,查阅很多资料,我认为《算法4》中介绍的Dijkstra双栈算法,相比别的实现非常简洁,且思路清晰,这里给出原版的java代码,有兴趣的同学可以对比实现(面对对象有API确实好用,用C++实现也好用)。
除此而外,我认为labuladong的做法也很轻巧,相比严版教材大篇幅的讲解更利于初学者理解,下面我们一步步解析用单栈实现计算器的过程。
【问题描述】输入一串合法的算式,由程序自动计算出结果
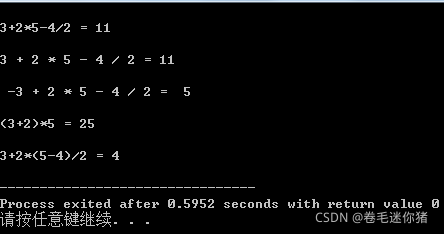
输入:3+2*(5-4)/2
输出:4
【思路】
(一)简化问题:
1.输入算式可以定性为string;
2.仅考虑四则运算和带括号的;
3.非法输入暂时不考虑。
大致的代码可以在纸上草拟一遍:
int caculate(char *expr) {
//step1 生成一个一个线性存储对象 list
List list = xxxxx;
//step2 填充字符数据到线性存储对象中
for(){
addElem(xxx, list);
}
//设计函数helper()具体执行计算,这个函数应该是递归和stack配合使用的
return helper(list);
}
如上方草稿,先保存原始数据,然后把保存对象交给具体执行函数计算算式结果。
(二)思考核心问题–helper()的设计
1.生成一个stack,用于压栈优先级低的计算式
2.类似于切香肠操作,一个字符一个字符的处理算式list=>自然想到removeFirst()这样的操作。
3.既然是切香肠,那么当香肠切完了,计算和相关递归工作就应该截止了=>得到循环截止条件:list->len == 0。
4.从list中切出一个字符后,首先判断是否为数值,如果是就将其转换为对应的数值变量。
5.由于“(”左括号的优先级最高,所以接下来就应该处理遇到左括号的情况:有了左括号,最佳额解决办法就是把剩余的list表达式再次扔给helper(),让其进入更深一层的递归调用中,递归出口就是遇到对应匹配的“)”右括号,这点在3-6 平衡括号问题中已讨论过。
6.【关键】如果当前处理字符,既不是数值也不是左括号,那么问题处理推理如下:
(1)不同于双栈处理计算式(一个符号栈,一个数值栈),单栈处理方案就应该只存储数值,符号放在栈外处理后再压栈-----这是处理方案的第一原则。
(2)如果符号是“+、-”(加、减号),那么可以把这个加减号合并到当待处理的数值中,处理完成后,新得到的数值压栈,具体来讲就是:加号和数值合并成新的正数,减号和数值合并成新的负数,很自然地解决了加减号问题。
(3)如果符号是“*、/”(乘、除号),根据优先级原则,应该立即和栈顶元素进行合并计算,并将计算结果再次压栈,这样就能完美解决单栈“只存数值,不存符号”的核心问题了。
其实正是以上(1)~(3)三点操作,保证了计算式的内部优先级问题。
if (xxxxx) {
//step1 压栈处理
if (sign == '+')
push(num, stack);
else if (sign == '-')
push(-num, stack);
else if (sign == '*')
push(topAndPop(stack) * num, stack);
else if (sign == '/')
push(topAndPop(stack) / num, stack);
//step2 符号sign更新
//step3 重置当前处理数值num
}
7.遇到“)”右括号,则本轮递归函数中大循环结束,准备计算最终结果。
8.如果计算式list遍历完成,那此时数值存储对象stack中仅包含生负数值,把这些数值累加起来不就是最后的原始计算式的期待的结果了吗?
综合以上逻辑设计,并调试代码细节,得到如下解决方案(打印调试语句被注释,可以打开方便理解代码运行机制):
int helper(List list) {
// printf("进入helper: list->len=%d", list->len);
// printList(list);
Stack stack = createStack();
char sign = '+';
int num = 0, res = 0;
while (list->len > 0) {
char c = removeFirst(list);
// printf("当前处理c=%c\n", c);
if (isdigit(c))
num = 10 * num + (c - '0');
if (c == '(')
num = helper(list);
if ((!isdigit(c) && c != ' ') || list->len == 0) {
if (sign == '+')
push(num, stack);
else if (sign == '-')
push(-num, stack);
else if (sign == '*')
push(topAndPop(stack) * num, stack);
else if (sign == '/')
push(topAndPop(stack) / num, stack);
sign = c;
num = 0;
}
if (sign == ')')
break;
}
// printList(list);
// printStack(stack);
while (!isEmpty(stack))
res += topAndPop(stack);
disposeStack(stack);
if (empty(list))
disposeList(list);
return res;
}
【完整解决方案】
1.main.c 为保证代码可读性,使用了少许库函数,list也可以用一个游标+数组去代替
#include 2.ArrayStack ArrayList 参考之前的博客内容不再贴出
3-8 迷宫问题(其实可以不用栈)
很多讲解数据结构的教材/教程(例如严版教材算法3.2 P50),都喜欢使用stack来解决迷宫问题(八皇后问题/N皇后问题也类似),但如果大一的C语言学的深入和扎实的话,自然会接触到基于递归的DFS(深度优先)/BFS(广度优先)的解决办法(这类递归的解决手段,本质也是依靠函数调用栈去“暂存”状态,还是用栈,哈哈),且简单好用,甚至有的同学会自学到更加优秀的解决方法,这些方法在后续的图论都会讨论到。因此个人认为使用stack解决迷宫问题作为一种思维训练是可以的,但算不上最优解。
多谈一句,如果真的想吃透迷宫问题(其实是很多工程问题的启蒙玩具模型),需要着手解决三个方面的问题:
(1)生成迷宫的算法和策略研究;
(2)走迷宫的算法和策略研究; ===>这就是很多数据结构教材中狭义的迷宫问题
(3)以上两个问题的可视化问题和策略研究。
但更快、更省、更优雅、更利于理解才是学习研究的核心。
接下来将慢慢地介绍思考和解决问题的过程,对于思路清晰的同学可能会感觉讲解的比较啰嗦,但我认为这种对细节琢磨对初学者来讲还是比较重要的,希望各位看官静心阅读。
【思路】
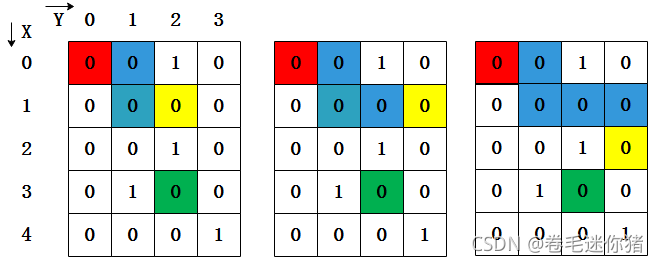
(一)我们将迷宫抽象: MAZE[X][Y] ==> 0 通路 , 1 障碍 , -1 已被访问过
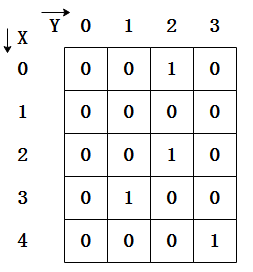
如上图,我们假设起点为(0,0),终点为(3,2),借助栈的记录特性尝试找到一种方法从红色格子,一步步移动到绿色格子
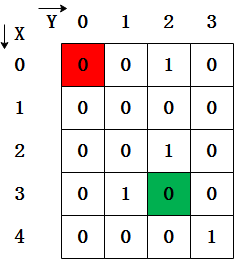
(二)我们规定:只能从上下左右四个方向中任意选择一个方向移动一步,可以设想下移动格子伪码
//curPos为当前走到的格子,tryPos为接下来尝试的格子,必然有
tryPos.x = curPos.x + NEXT.x;
tryPos.y = curPos.y + NEXT.y;
这里的NEXT可以抽象成表示位移矩阵

自然上面的伪码可以改为
![]()
(三)移动的规则。按照优先级可以编排如下逻辑
step1 检查当前位置curPos的坐标是否与终点重合,如果重合了程序就可以结束了。
step2 如果没有到达出口,那么可以按照“右=>下=>左=>上”的顺序挨个尝试“下一步”。
接下来思考第一个核心问题:如何表现尝试的结果呢?
答:可以使用stack的压栈功能(push)保存“当前位置”,那么当前的“下一步”就变成接下来探索的“当前位置”了;如果“当前位置”尝试所有“下一步”都失败了,可以使用stack的出栈功能(pop)将不可用的格子排除出最终路径记录(stack)中。若想明白上了面的描述,就继续补齐我们的逻辑:
step3 如果下一步可达(不越界,格子上的值是0,为通路),当前位置压栈,继续尝试下一步。
step4 如果尝试了所有下一步都不可达,当前位置标记为-1,表明已经走过(如果不标记,那么问题规模是不可能收敛的,每一步都可能走“回头路”,来来回回永远死循环!);同时当前位置出栈。
上面step1~step3基本上解决了怎么走,如何走的问题,但还有第二个核心问题:
按照上面逻辑,如果迷宫是能走通的,自然不用担心;可是如果迷宫无解呢?以上的步骤应该是一个不断尝试的大循环,不能限制的走下去,出口在哪?
答:很容易想到,每次尝试都有格子压榨/出栈,只要栈不为空,说明还有格子没有尝试到;反过来想,如果所有格子都出栈了,不再有新的格子(未尝试过的)压栈,说明所有的格子已经都走了一遍;所以判断大循环结束的条件应该是查看当前路径记录stack是否为空。
【解决方案】
对上面每个逻辑细节想明白之后,就可以开始编码了,先借助上面的描述写出可用的stack工具
- ArrayStack.h
#ifndef _ARRAY_STACK_H
#define _ARRAY_STACK_H
#define EMPTY_TOS (-1)
#define DEFAULT_CAPACITY (100)
#define OK (0)
#define ERROR (-1)
typedef struct POSITION{
int x;
int y;
int direction;
} ElementType;
struct StackRecord {
int capacity;
int topIndex;
ElementType *array;
};
typedef struct StackRecord *Stack;
int isEmpty(Stack S);
int isFull(Stack S);
Stack createStack();
void disposeStack(Stack S);
void makeEmpty(Stack S);
void push(ElementType X, Stack S);
ElementType* peek(Stack S);
void pop(Stack S);
void printStack(Stack S);
void nextDirection(Stack S);
#endif
与之前的代码有少许不同:
(1)ElementType更改为POSITON结构体,原来我们使用的是最简单的int,所以此处我们简化学习的弊端也体现出来了,没有考虑工具栈的通用性,但实际解决并不麻烦;
typedef struct POSITION{
int x;
int y;
int direction;
} ElementType;
(2)如何记录当前点下一步应该尝试哪个方向的位移呢,直接在POSITION结构体中配置一个方向标记direction,默认初始值0,即按照之前设计好的“右=>下=>左=>上”的顺序运动。正好可以把“尝试所有方向”的逻辑判断直接转化为对direction大小的判断
if(curPos->direction < 4){
//尝试所有方向,当前位置压栈
//一个方向的下一步不可用,direction++,继续下一个方向
} else {
//尝试都失败了,出栈
}
(3)在上面的(2)中,提到了要对当前位置(栈顶元素)的下一个尝试方++
curPos->direction++;
也就是修改栈顶元素的属性,那么之前的代码中,通过函数top()
ElementType top(Stack S){
return isEmpty(S) ? INT_MIN : S->array[S->topIndex];
}
获取栈顶元素的方法就设计得不合理了,需要直接交给用户栈顶元素的指针,直接在对应地址空间上修改direction才行,这也是之前为了聚焦stack各种操作本质,放弃去ElementTpye通用性研究的缺陷,不过可以直接改进。有心的同学参考文献资料[x]把现有stack全面升级一遍,强化对指针/地址的理解。
ElementType* peek(Stack S){
return isEmpty(S) ? NULL : &S->array[S->topIndex];
}
- ArrayStack.c
#include 先比之前的实现,除了peek()替换了top(),printStack()也做了少许改进,方便后续呈现运动路径。
- main.c
#include 在3-8开头的讨论中,提到了迷宫的自动生成也是一个值得本科学生研究的问题,在本帖中从简化问题的角度出发,将很多数据都写成了全局变量,同学们可以自己改的更加规范些,但我觉得注意力应该放在对自己设计逻辑的编码实现和调试中;相关的必要注释已经将代码解释的很清楚了
3-9 最小栈(双栈的第一次使用)
(参考《漫画算法》)
【问题描述】实现一个栈,该栈带有出栈(pop)、入栈(push)、取最小元素(getMin)3个方法,要求保证这3个方法的时间复杂度都是O(1)。
- 【思路简介】
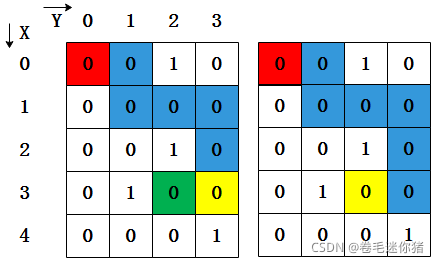
按照原始的stack设计,获取栈内最少元素的操作时间复杂度必定是O(n),自然想到需要预处理,回到“空间换时间”的老套路上。如下图所示,主栈+辅助栈策略的就能实现这个功能:
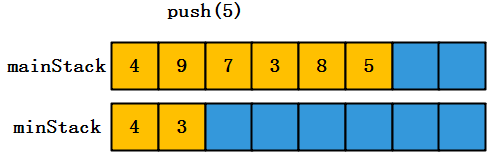
(1)开始的时候,mainStack和minStack都没有元素,两个栈都执行push,操作时间复杂度为O(1)
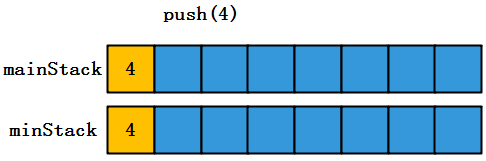
(2)mainStack中不再为空,那么需要和minStack栈顶元素(4)进行比较,如果小了,那么需要将新元素push到minStack中,同时mainStack依旧执行压栈操作。

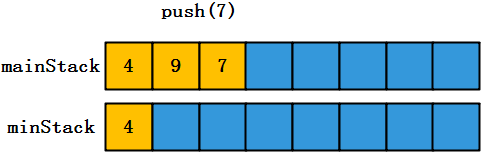
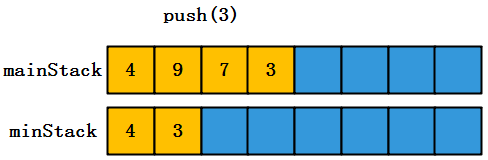

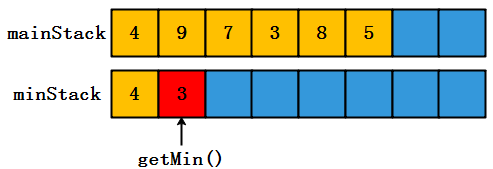
(3)执行getMin()操作,仅需要top()操作返回minStack栈顶元素即可,时间复杂度为O(1)
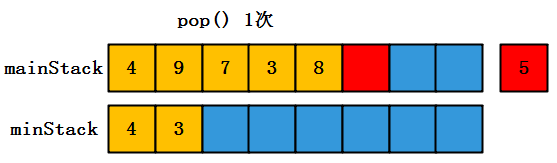
(4)出栈操作需要保证mainStack和minStack的元素一致性,也就是说如果mainStack和minStack的栈顶元素一致,那么minStack也需要执行pop操作。
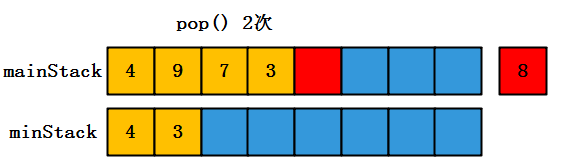
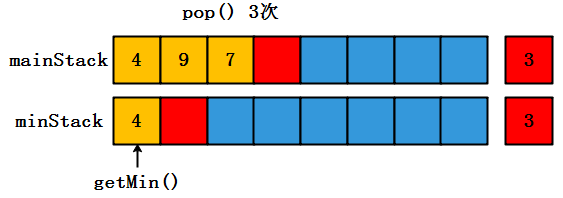
(两个栈的栈顶元素一致,需要同时出栈) - 代码实现
(1)ArrayStack参考之前实现,不再贴出
(2)MinStack.h 定义我们自己的最小栈(没有面对对象真的不顺手 = 3 =)
#ifndef _MIN_STACK_H
#define _MIN_STACK_H
#include "ArrayStack.h"
struct MinStackRecord {
Stack minStack;
Stack mainStack;
};
typedef struct MinStackRecord *MinStack;
MinStack createMinStack();
ElementType _pop(MinStack stack); //注意不要和原始实现重名,下同
void _push(ElementType data, MinStack stack);
ElementType getMin(MinStack stack); //转了一大圈就为它
#endif
(3)MinStack.c 具体实现,注意topAndPo()和pop()的区别
#include (4)main.c 测试代码
#include 3-10 单调栈(正向/反向栈)
【问题描述】“下一个更大元素I”:输入一个数组,返回一个等长的数组,对应索引存储着下一个更大元素,如果没有更大的元素则存-1。(转至labuladong的算法小抄)例如:
输入:nums = [2, 1, 2, 4, 3]
输出:nums = [4, 2, 4,-1,-1]
注:此问题参考labuladong的算法小抄。
【思路】
(1)如果使用扫描的方式完解决这个问题,类比常用排序算法需要扫描一遍,时间复杂度为 O ( n 2 ) O(n^2) O(n2)
(2)转变思维,咱们从最简单的部分入手:
<1>从后往前走,先解决index = len-1的元素对应的“next greater”,自然为-1,接着利用stack压栈最后一个元素,把最后一个元素作为“挡板”;
<2>接着比较倒数第二个元素和stack的栈顶“挡板”,如果符合条件,则“更换”挡板(出栈一次,压栈一次,且压栈是必做操作);
<3>循环往复,直到第0个元素(index = 0)的结果计算出来。

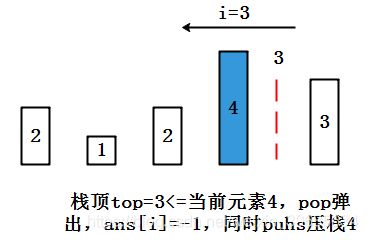
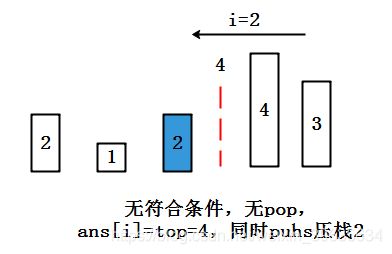
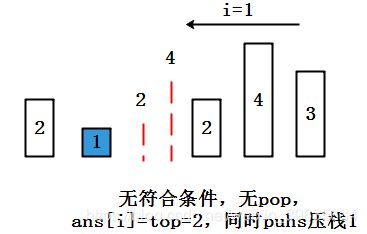
接下来就是非常有意思的“换挡板”工作了

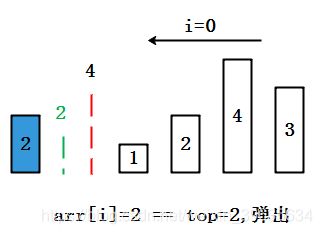

上代码(ArrayStack参考之前实现,不再贴出)
#include 输出结果:

如果是求间隔呢?如果是环形数组呢?这些问题在labuladong的算法小抄里也都有讨论,我们就不列出来了,大家有余力一定要买一本自己看哦!
至于如何使用栈去实现队列,将放在队列一章中讲解。
后记:这篇博客拖了很久,主要是
(1)家里添宝宝了,望各位同学见谅。
(2)假期除了安胎,还做了一些蓝桥培训。
(3)加入了迷宫问题,还要兼顾各种算法(特别是DFS和BFS),外加考虑使用可视化的方式呈现,反复思考之后认为还是分开讲比较好。
所以就慢了,望各位同学见谅。
外记:学校的教改目前是推不动了(2021年立个flag),地方院校懂得都懂,只能靠诸位朋友和同学们在社区和论坛上开辟第二战场学习了,无奈,真的很无奈。
[1] 《labuladong的算法小抄》
[2] 《漫画算法》
[3] C语言实现栈(基于结构体指针)