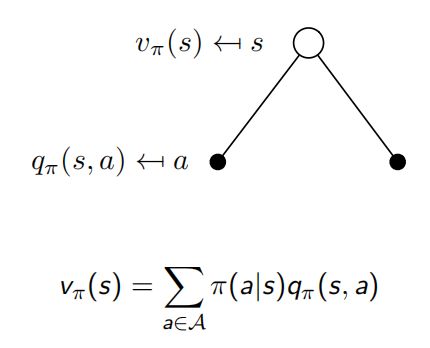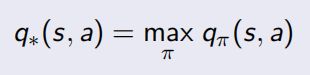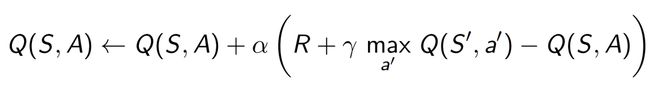- 这是新开的一个系列,将结合理论和部分代码(by ElegantRL)介绍强化学习中的算法,将从基础理论总结到现在常用的SAC,TD3等算法,希望能帮助大家重温知识点。本文是第一部分,将从基础理论讲解到DQN的各种变体。
目录
- 基础理论复习
- Q-learning
- Sarsa
- DQN
- Prioritized Experience Replay
- Double DQN
- Dueling DQN
- Noisy Network
- 其他
- 参考
基础理论复习
- 强化学习简单来说就是智能体agent根据当前的状态state输出动作action,与环境env进行交互获取奖励reward来迭代更新寻求获得最大回报return的过程。接下来主要复习几个重要的公式,熟悉的读者跳过即可。
贝尔曼方程
- 首先是大家熟悉的贝尔曼方程,贝尔曼方程是对状态价值的期望,即计算某一状态下预期会获得多少reward,从公式可以看出我们衡量一个状态的价值可以通过离开这个状态得到的即时奖励加上对后续状态价值的期望得到。

- 同理这个方程在已知环境状态转移概率的情况下还有另一个写法,结合下面这个图很容易理解:

动作价值函数
- 其次是动作价值函数,动作价值函数就是对某个状态下采取某个动作的期望,即计算某一状态下采取某个动作预期会获得多少reward(注意这里采取不同的策略得到的动作价值函数不同):

- 当然动作价值函数和状态价值函数之间是有联系的,因为每个状态都是采取了动作才到达下一个状态,所以:
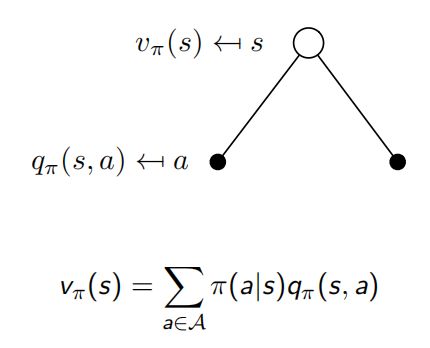
最优动作价值函数
- 前面提到动作价值函数的值会根据采取的策略不同而改变,那我们怎么才能排除策略的影响,只评价当前动作的价值呢?解决方案就是最优动作价值函数,最优动作价值函数即是所有策略下产生的众多动作价值函数中的最大者:
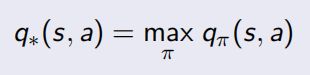
最优状态价值函数
- 同样最优状态价值函数是所有策略下产生的众多状态价值函数中的最大者:

- 最优状态价值函数和最优动作价值函数之间同样也有关系:


强化学习中的随机性
- 这一点非常重要,我们要清楚强化学习中随机性的来源:策略函数和状态转移函数,这对之后的学习很有帮助。
- 动作的随机性来自于策略函数。给定当前的状态 s s s,策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s)会算出动作空间中每个动作 a a a的概率值。智能体agent执行的动作是随机抽样的结果,所以带有随机性。

- 状态的随机性来自于状态转移函数,即当状态 s s s和动作 a a a都被确定下来,下一个状态仍然有随机性。我们的环境用状态转移函数 p ( s ′ ∣ s , a ) p(s^{'}|s,a) p(s′∣s,a)计算所有可能状态的概率,然后做随机抽样,得到新的状态。

Q-learning
- 我们从value-based的表格式算法开始总结,第一个就是Q-learning。
算法流程
- 表格式算法即用一个表格去存储不同状态下不同行为对应的Q价值,如下图所示:
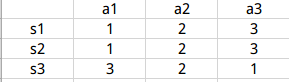
- 具体表格中的每个Q值更新的公式如下:
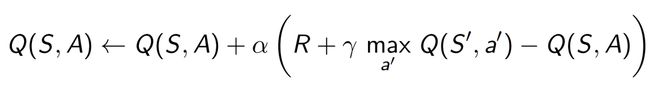
- 算法流程简单来说就是先随机初始化获得一个状态 s s s,在当前状态 s s s下根据 ϵ \epsilon ϵ-greedy策略选择一个动作 a a a,然后执行我们选择的动作 a a a与环境交互,获取下一个状态 s ′ s^{'} s′,并得到 s ′ s^{'} s′的即时回报 R R R,这时我们会更新我们初始状态行为对的Q值 Q ( s , a ) Q(s,a) Q(s,a),我们更新公式中的$ max_{a’}Q(s^{’}, a{’})$即使用下一个状态$s{’} 中 对 应 价 值 最 大 的 动 作 的 Q 值 进 行 更 新 , 注 意 这 里 只 是 更 新 , 并 不 会 真 的 执 行 这 个 价 值 最 大 的 动 作 。 这 里 的 更 新 策 略 ( 评 估 策 略 ) 与 我 们 的 行 为 策 略 ( 中对应价值最大的动作的Q值进行更新,注意这里只是更新,并不会真的执行这个价值最大的动作。这里的更新策略(评估策略)与我们的行为策略( 中对应价值最大的动作的Q值进行更新,注意这里只是更新,并不会真的执行这个价值最大的动作。这里的更新策略(评估策略)与我们的行为策略(\epsilon$-greedy)不同,这种算法我们也称为off-policy算法。

TD算法
- 我们注意到,我们算法更新公式中的核心 ( R + γ m a x a ′ Q ( S ′ , a ′ ) − Q ( S , A ) ) (R + \gamma max_{a'}Q(S^{'}, a^{'}) - Q(S,A)) (R+γmaxa′Q(S′,a′)−Q(S,A)),两项的差值显然是在计算误差,那这是在计算什么误差?为什么这么计算误差就是对的?
- 我们一般把 R + γ m a x a ′ Q ( S ′ , a ′ ) R + \gamma max_{a'}Q(S^{'}, a^{'}) R+γmaxa′Q(S′,a′)称为TD-Target,把 ( R + γ m a x a ′ Q ( S ′ , a ′ ) − Q ( S , A ) ) (R + \gamma max_{a'}Q(S^{'}, a^{'}) - Q(S,A)) (R+γmaxa′Q(S′,a′)−Q(S,A))称为TD-Error。
- 我们回到我们算法的本质,在valued-based的背景下,我们之所以要设计一个算法,是为了能衡量不同状态下采取不同动作的价值,如果我们能准确知道每个状态下每个动作的价值,那我们在不同的状态下只要采取价值最高的动作,那我们预期得到的reward就会最多。但是现实情况下,因为迭代次数有限等等的原因,我们很难准确知道每个状态行为对的价值,这时候我们就需要通过估计的手段去近似这个价值。
- 我们知道 Q ( S , A ) Q(S,A) Q(S,A)是我们估计的在状态 S S S下采取动作 A A A的价值,这个价值是我们从表格近似得到的,而 R + γ m a x a ′ Q ( S ′ , a ′ ) R + \gamma max_{a'}Q(S^{'}, a^{'}) R+γmaxa′Q(S′,a′)是我们执行了动作后实际获得的奖励 R R R加上后续状态的估计 γ m a x a ′ Q ( S ′ , a ′ ) \gamma max_{a'}Q(S^{'}, a^{'}) γmaxa′Q(S′,a′),前者是纯估计,后者是实际得到的奖励+估计,可以把他称为部分估计,部分估计因为有事实的部分,所以一定会比纯估计要更准确,所以我们训练算法的时候让TD-Error变小的过程就是让我们估计的 Q ( S , A ) Q(S,A) Q(S,A)逼近TD-Target的过程,也就是让我们不准确的“全估计”逼近更准确的“部分估计”的过程。
bootstrap
- bootstrap直译过来即为自举,在强化学习当中的意思就是我们用自己做出的估计去更新别的同类的估计,比如我们上面总结Q-learning算bootstrap法时,我们使用下一状态的最优动作价值去更新这一状态的动作价值,这就是bootstrap。
- bootstrap的好处是方差比较小,算法容易收敛。坏处则是有偏差,因为我们是用估计去更新估计,如果我们后一状态的估计本身是高估或者低估的,那么这种更新就会让偏差传递到前一个状态的价值估计。
Sarsa
- Sarsa算法和Q-learning算法极为相似,表格中每个状态对应的动作Q值更新公式如下:

- 算法流程和Q-learning基本一致,唯一变化的地方是根据 ϵ \epsilon ϵ-greedy策略选择了一个动作进入了下一个状态后,Sarsa继续根据 ϵ \epsilon ϵ-greedy策略选择下一个动作执行并用这个动作更新,这里我们的更新策略(评估策略)与我们的行为策略都是 ϵ \epsilon ϵ-greedy策略,这种算法我们也称为on-policy策略。
DQN
- 前面总结的Sarsa和Q-learning都是基于表格的value-based的算法,基于表格的算法在对于现实场景下高维度的状态和动作空间很难处理,因此和深度学习的结合显得理所当然,DQN也是在此契机被提出来。
构造损失函数
- 既然我们要结合深度学习,那就需要构造损失函数进行训练,回想之前Q-learning的更新公式,其中的核心部分是TD-Target减去Q(S,A),TD-Target是比Q(S,A)更准确的估计,可以当做true-label,把Q(S,A)当做我们的predict-label,这样我们的损失函数就构造出来了: L ( w ) = 1 2 [ Q ( s t , a t ; w ) − T D − T a r g e t ] 2 L(w) = \frac{1}{2} [Q(s_t,a_t;w) - TD-Target] ^ 2 L(w)=21[Q(st,at;w)−TD−Target]2
Experience Replay Buffer
- 我们知道深度学习要求我们的输入数据是独立同分布(independent and identically distributed,i.i.d.),而在强化学习当中,因为数据(数据格式一般为:state, action, reward, next_state)之间是有关联的,所以我们不能像深度学习一样直接输入进网络。因此我们把需要的数据保存起来,保存进我们的经验池当中,当经验池中的数据足够多时,随机抽样得到的数据就能接近i.i.d.。
- 这里要提一下ElegantRL中对于Replay Buffer的优化:1.把Replay Buffer 的数据都放在连续的内存里,经过实验这种方法最快 2.按trajectory的顺序保存 env transition,避免重复保存next state,next state只需要在下一个索引的地方就能取到 3.分开保存 state 与其他数据,减少图片数据flatten的麻烦 4.将off-policy 的数据一直保存在显存内 5.保存能简化计算的变量, 保存mask = gamma if done else 0 用于计算Q值,而不是保存 done 6.为on-policy 的PPO 算法保存 noise 用于计算新旧策略的熵 具体可以看DRL的经验回放(Experience Replay Buffer)的三点高性能修改建议
- 当然,经验池也是有局限的,只有off-policy的算法可以使用经验池,因为我们经验池里面存的数据都是用行为策略采集的。如果是on-policy算法,经验池里存的就是过时的评估策略,和当前的评估策略不同,是过时的,所以不可以使用经验池。
DQN的高估问题及目标网络
- DQN产生高估的原因有两个:第一,自举bootstrap导致偏差的传播,这个前面分析过;第二,我们更新Q值过程中的最大化会导致 TD-Target高估真实价值。为了缓解高估,需要从导致高估的两个原因下手,改进DQN,而使用目标网络就是从切断自举这个角度来避免高估。
- 回顾一下,原始DQN是这样计算TD-Error: ( R + γ m a x a ′ Q ( s ′ , a ′ ; w ) − Q ( s , a ; w ) ) (R + \gamma max_{a'}Q(s^{'}, a^{'};w) - Q(s,a;w)) (R+γmaxa′Q(s′,a′;w)−Q(s,a;w)),然后通过梯度下降更新 w w w,使得 Q ( s , a ; w ) Q(s,a;w) Q(s,a;w)越来越接近TD-Target。想要切断bootstrap带来的偏差,可以用另一个网络计算TD-Target,而不是用DQN自己计算TD-Target。另一个网络就叫做目标网络(Target Network),把他记做 Q ( s , a ; w − ) Q(s,a;w^{-}) Q(s,a;w−),它的神经网络结构与 DQN 完全相同,但是参数和原始参数不同。
算法流程

- 使用Target-Network虽然可以缓解bootstrap带来的偏差,但是却不能完全解决这个问题,因为目标网络的参数仍然与 DQN 相关。
代码
- 以下代码来自ElegantRL,非常优雅,相信读者一看就懂
class AgentDQN(AgentBase):
def __init__(self):
super().__init__()
self.explore_rate = 0.1
self.action_dim = None
def init(self, net_dim, state_dim, action_dim):
self.action_dim = action_dim
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.cri = QNet(net_dim, state_dim, action_dim).to(self.device)
self.cri_target = deepcopy(self.cri)
self.act = self.cri
self.criterion = torch.torch.nn.MSELoss()
self.cri_optimizer = torch.optim.Adam(self.cri.parameters(), lr=self.learning_rate)
def select_action(self, state) -> int:
if rd.rand() < self.explore_rate:
a_int = rd.randint(self.action_dim)
else:
states = torch.as_tensor((state,), dtype=torch.float32, device=self.device).detach_()
action = self.act(states)[0]
a_int = action.argmax().cpu().numpy()
return a_int
def explore_env(self, env, buffer, target_step, reward_scale, gamma) -> int:
for _ in range(target_step):
action = self.select_action(self.state)
next_s, reward, done, _ = env.step(action)
other = (reward * reward_scale, 0.0 if done else gamma, action)
buffer.append_buffer(self.state, other)
self.state = env.reset() if done else next_s
return target_step
def update_net(self, buffer, target_step, batch_size, repeat_times) -> (float, float):
buffer.update_now_len_before_sample()
next_q = obj_critic = None
for _ in range(int(target_step * repeat_times)):
with torch.no_grad():
reward, mask, action, state, next_s = buffer.sample_batch(batch_size)
next_q = self.cri_target(next_s).max(dim=1, keepdim=True)[0]
q_label = reward + mask * next_q
q_eval = self.cri(state).gather(1, action.type(torch.long))
obj_critic = self.criterion(q_eval, q_label)
self.cri_optimizer.zero_grad()
obj_critic.backward()
self.cri_optimizer.step()
self.soft_update(self.cri_target, self.cri, self.soft_update_tau)
return next_q.mean().item(), obj_critic.item()
class QNet(nn.Module):
def __init__(self, mid_dim, state_dim, action_dim):
super().__init__()
self.net = nn.Sequential(nn.Linear(state_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, action_dim))
def forward(self, state):
return self.net(state)
Prioritized Experience Replay
- 优先经验回放 (Prioritized Experience Replay) 是一种特殊的经验回放方法,它比普通的经验回放效果更好:既能让收敛更快,也能让收敛时的平均回报更高。
- 原来的经验回放是从经验池当中均匀抽样出来样本进行更新,但其实这是有问题的,因为不同样本的重要性是不同的,这里的越重要指的是预测的 Q ( S , A ) Q(S,A) Q(S,A)离TD-Target越远(TD-Error越大),即你预测的Q值越不准我自然越要拿你出来更新让你变准。
- 优先经验回放对经验池的样本做非均匀抽样,对经验池里的每个样本都赋予一个权重,权重即是TD-Error的绝对值 ∣ δ i ∣ |\delta_i| ∣δi∣,它的抽样概率取决于TD-Error。有两种方法设置抽样概率,一种是: p i = ∣ δ i ∣ + ϵ p_i = |\delta_i| + \epsilon pi=∣δi∣+ϵ
- 此处的 ϵ \epsilon ϵ是个很小的数,防止抽样概率接近零,用于保证所有样本都以非零的概率被抽到。第二种是先将 δ i \delta_i δi做降序排列,然后计算: p i = 1 r a n k ( i ) p_i = \frac{1}{rank(i)} pi=rank(i)1
- 这里的rank(i)是 δ ( i ) \delta(i) δ(i)的序号,大的 δ ( i ) \delta(i) δ(i)序号小,小的 δ ( i ) \delta(i) δ(i)序号大。
- 优先经验回放做非均匀抽样,导致不同的样本抽样概率不同,改变了样本分布,而我们一开始引起经验回放就是为了要独立同分布的数据进行训练,所以优先经验回放必然引起偏差。应该相应调整学习率,抵消掉不同抽样概率造成的偏差。如果一条样本被抽样的概率大,那么它的学习率就应该比较小。可以这样设置学习率: α i = α ( b ∗ p i ) β \alpha_i = \frac{\alpha}{(b * p_i)^\beta} αi=(b∗pi)βα
- 此处的b是经验池样本的总数, β \beta β是一个范围在0到1的超参数,需要调整。
- 这里要注意,抽样概率和学习率之间的变化并不会抵消。比如当 β \beta β=1时,如果抽样概率 p i p_i pi变大10倍,从公式来看那学习率就减少10倍,看起来似乎两者的变化抵消了,但其实并不是。两种情况并不等价:
- 设置学习率为1,使用样本a计算10次梯度,更新十次参数 w w w
- 设置学习率为10,使用样本a计算1次梯度,更新一次参数 w w w
- 其实第二种方式是对样本更有效的利用。第二种方式的缺点在于计算量大了十倍;所以第二种方式只被用于重要的样本。

Double DQN
- 前面分析DQN会高估的时候说了两个原因:第一,自举bootstrap会导致偏差的传播;第二,我们更新Q值过程中的最大化会导致 TD-Target高估真实价值。前面提到使用目标网络可以缓解bootstrap导致的偏差,但是无助于缓解最大化造成的高估,这个小节介绍Double DQN就是在目标网络的基础上,缓解最大化造成的高估。
- 那我们该如何缓解最大化造成的高估呢?我们回想一下前面使用目标网络的思路,为了缓解bootstrap造成的偏差,让计算TD-Target和计算 Q ( s , a ) Q(s,a) Q(s,a)的网络不为同一个。那这种思路是否能用来缓解最大化造成的高估呢?显然是可以的。
- 我们可以把计算TD-Target分为两步,第一步是通过最大化选择动作 a r g m a x Q ( s , a ; w ) argmax Q(s,a;w) argmaxQ(s,a;w),第二步则是求值 y = R + γ Q ( s , a ; w ) y = R + \gamma Q(s,a;w) y=R+γQ(s,a;w),沿用之前的思路,我们只要把选择动作的网络和求值的网络区分开,一个用原本的网络,一个用目标网络,自然就可以缓解最大化造成的高估。
- 当然也还有另一个思路,就是同时训练两个Q network并选择较小的Q值用于计算TD-error,降低高估误差。
代码
- ElegantRL采取第二种思路的写法,具体如下:
class AgentDoubleDQN(AgentDQN):
def __init__(self):
super().__init__()
self.explore_rate = 0.25
self.softmax = torch.nn.Softmax(dim=1)
def init(self, net_dim, state_dim, action_dim):
self.action_dim = action_dim
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.cri = QNetTwin(net_dim, state_dim, action_dim).to(self.device)
self.cri_target = deepcopy(self.cri)
self.act = self.cri
self.criterion = torch.nn.SmoothL1Loss()
self.cri_optimizer = torch.optim.Adam(self.act.parameters(), lr=self.learning_rate)
def select_action(self, state) -> np.ndarray:
states = torch.as_tensor((state,), dtype=torch.float32, device=self.device).detach_()
actions = self.act(states)
if rd.rand() < self.explore_rate:
action = self.softmax(actions)[0]
a_prob = action.detach().cpu().numpy()
a_int = rd.choice(self.action_dim, p=a_prob)
else:
action = actions[0]
a_int = action.argmax(dim=0).cpu().numpy()
return a_int
def update_net(self, buffer, target_step, batch_size, repeat_times) -> (float, float):
buffer.update_now_len_before_sample()
next_q = obj_critic = None
for _ in range(int(target_step * repeat_times)):
with torch.no_grad():
reward, mask, action, state, next_s = buffer.sample_batch(batch_size)
next_q = torch.min(*self.cri_target.get_q1_q2(next_s))
next_q = next_q.max(dim=1, keepdim=True)[0]
q_label = reward + mask * next_q
act_int = action.type(torch.long)
q1, q2 = [qs.gather(1, act_int) for qs in self.cri.get_q1_q2(state)]
obj_critic = self.criterion(q1, q_label) + self.criterion(q2, q_label)
self.cri_optimizer.zero_grad()
obj_critic.backward()
self.cri_optimizer.step()
self.soft_update(self.cri_target, self.cri, self.soft_update_tau)
return next_q.mean().item(), obj_critic.item() / 2
Dueling DQN
- Dueling DQN提出了优势函数,优势函数定义为动作价值函数减去状态价值函数,即: A ( s , a ) = Q ( s , a ) − V ( s , a ) A(s,a) = Q(s,a) - V(s,a) A(s,a)=Q(s,a)−V(s,a)
- 为什么要提出优势函数?我们知道状态价值函数表示某个状态有多好,同时状态价值函数也是动作价值函数的期望,反映了这个状态下的平均动作价值。动作价值函数表示在这个状态下选择某个动作有多好。那么优势函数可以认为是某个动作重要性的相对度量,即选择这个动作相对于平均动作水平来说更好或者更差。
- 具体结构如下:先共享卷积层,然后接上两个全连接层,一个输出优势,一个输出状态价值,最后做个加法就得到每个动作的价值。

- 在某些状态下,采取不同的行为并不会对Q值造成多大的影响,因此Dueling DQN 结合了 优势函数估计的Q值 与 原本DQN对不同动作估计的Q值。使得在某些状态下,Dueling DQN 能在只收集到一个离散动作的数据后,直接得到准确的估值。当某些环境中,存在大量不受动作影响的状态,此时Dueling DQN能学得比DQN更快。
解决不唯一性
- 如果我们直接用$ Q(s,a) = A(s,a)+ V(s,a)$进行学习训练,会发现训练过程不稳定,因为这样A和V可以随意上下波动而不影响Q,比如A增加100,V减少100,对于Q值没有影响,这就意味着 V 和 D 的参数可以很随意地变化,却不会影响输出,所以我们需要约束这种情况。
- 一般我们的做法是减去一个项恒等于零的 m a x A ( s , a ′ ; θ , α ) max A(s,a^{'};\theta,\alpha) maxA(s,a′;θ,α),这样就可以让训练稳定:

- 但是作者发现用均值替代更好,所以最后变成:

代码
- 一般而言,我们会把Double DQN和Dueling DQN一起结合,这样效果更好,代码如下:
class AgentD3QN(AgentDoubleDQN):
def __init__(self):
super().__init__()
def init(self, net_dim, state_dim, action_dim):
"""Contribution of D3QN (Dueling Double DQN)
There are not contribution of D3QN.
Obviously, DoubleDQN is compatible with DuelingDQN.
Any beginner can come up with this idea (D3QN) independently.
"""
self.action_dim = action_dim
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.cri = QNetTwinDuel(net_dim, state_dim, action_dim).to(self.device)
self.cri_target = deepcopy(self.cri)
self.act = self.cri
self.criterion = torch.nn.SmoothL1Loss()
self.cri_optimizer = torch.optim.Adam(self.act.parameters(), lr=self.learning_rate)
class QNetTwinDuel(nn.Module):
def __init__(self, mid_dim, state_dim, action_dim):
super().__init__()
self.net_state = nn.Sequential(nn.Linear(state_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, mid_dim), nn.ReLU())
self.net_val1 = nn.Sequential(nn.Linear(mid_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, 1))
self.net_val2 = nn.Sequential(nn.Linear(mid_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, 1))
self.net_adv1 = nn.Sequential(nn.Linear(mid_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, action_dim))
self.net_adv2 = nn.Sequential(nn.Linear(mid_dim, mid_dim), nn.ReLU(),
nn.Linear(mid_dim, action_dim))
def forward(self, state):
t_tmp = self.net_state(state)
q_val = self.net_val1(t_tmp)
q_adv = self.net_adv1(t_tmp)
return q_val + q_adv - q_adv.mean(dim=1, keepdim=True)
def get_q1_q2(self, state):
tmp = self.net_state(state)
val1 = self.net_val1(tmp)
adv1 = self.net_adv1(tmp)
q1 = val1 + adv1 - adv1.mean(dim=1, keepdim=True)
val2 = self.net_val2(tmp)
adv2 = self.net_adv2(tmp)
q2 = val2 + adv2 - adv2.mean(dim=1, keepdim=True)
return q1, q2
Noisy network
- Noisy network通过添加噪声有效地加强算法的探索能力。假设原来网络的参数为 w w w,现在就变成 μ + σ ⊙ ξ \mu + \sigma \odot \xi μ+σ⊙ξ, μ \mu μ是 w w w的均值, σ \sigma σ是 w w w的标准差,前两个参数是可学习的参数, ξ \xi ξ是随机生成的噪声,生成的方式分为独立高斯噪音和分解高斯噪音。
- 我们一般在最后输出层的最后一两层加入噪声进行训练,噪声网络主要有两点优点:第一,在权重上加入噪音带来的不确定性,比在策略上加噪声探索力度更大( ϵ − g r e e d y \epsilon-greedy ϵ−greedy)。第二,噪音的标准差也是学习的参数,网络通过学习可以调整噪音的大小。

其他
- 当然DQN还有其他变体,比如Distributional DQN(把传统DQN中的value function换成了value distribution,从预测价值变成预测价值的分布),使用分布式等等,这部分有空再补上。
参考
- https://github.com/wangshusen/DRL
- https://github.com/AI4Finance-LLC/ElegantRL