Query-Efficient Hard-label Black-box Attack: An Optimization-based Approach论文解读

Abstract

We study the problem of attacking a machine learning model in the hard-label black-box setting, where no model
information is revealed except that the attacker can make queries to probe the corresponding hard-label decisions. This
is a very challenging problem since the direct extension of state-of-the-art white-box attacks (e.g., C&W or PGD) to the
hard-label black-box setting will require minimizing a non-continuous step function, which is combinatorial and cannot
be solved by a gradient-based optimizer. The only current approach is based on random walk on the boundary [1],
which requires lots of queries and lacks convergence guarantees. We propose a novel way to formulate the hard-label
black-box attack as a real-valued optimization problem which is usually continuous and can be solved by any zeroth order optimization algorithm. For example, using the Randomized Gradient-Free method [2], we are able to bound the
number of iterations needed for our algorithm to achieve stationary points. We demonstrate that our proposed method
outperforms the previous random walk approach to attacking convolutional neural networks on MNIST, CIFAR, and
ImageNet datasets. More interestingly, we show that the proposed algorithm can also be used to attack other discrete
and non-continuous machine learning models, such as Gradient Boosting Decision Trees (GBDT).

1 Introduction

In this paper, we develop an optimization-based framework for attacking machine learning models in a more realistic
and general “hard-label black-box” setting. We assume that the model is not revealed and the attacker can only make
queries to get the corresponding hard-label decision instead of the probability outputs (also known as soft labels).Attacking in this setting is very challenging and almost all the previous attacks fail due to the following two reasons.
First, the gradient cannot be computed directly by backpropagation, and finite differences based approaches also fail
because the hard-label output is insensitive to small input perturbations; second, since only hard-label decision is
observed, the attack objective functions become discontinuous with discrete outputs, which is combinatorial in nature
and hard to optimize (see Section 2.4 for more details).

In this paper, we make hard-label black-box attacks possible and query-efficient by reformulating the attack as a
novel real-valued optimization problem, which is usually continuous and much easier to solve. Although the objective
function of this reformulation cannot be written in an analytical form, we show how to use model queries to evaluate its
function value and apply any zeroth order optimization algorithm to solve it. Furthermore, we prove that by carefully
controlling the numerical accuracy of function evaluations, a Random Gradient-Free (RGF) method can convergence to
stationary points as long as the boundary is smooth. We note that this is the first attack with a guaranteed convergence
rate in the hard-label black-box setting. In the experiments, we show our algorithm can be successfully used to attack
hard-label black-box CNN models on MNIST, CIFAR, and ImageNet with far less number of queries compared to the
state-of-art algorithm.

2 Background and Related work

We will first introduce our problem setting and give a brief literature review to hightlight the difficulty of attacking
hard-label black-box models.

2.1 Problem Setting

设本文所用的判别器为$f:{\mathbb{R}}^d\to \{1,\dots ,K\}$，原始数据样本为$x_0$，最终目标是生成满足如下关系的对抗样本$x$：

$$x\text{is close to }{x}_0\text{and}f(x)\ne f(x_0)(x\text{is misclassified by model}f)(1)$$

2.2 白盒攻击

大多数攻击算法都关注于白盒攻击，即整个判别器$f$都暴露给了攻击者。对于这种设定下的神经网络，因为网络结构和参数都暴露给了攻击者，那么我们就可以在目标模型上进行反向传播。对于神经网络分类器来讲，我们通常设定$f(x)=\underset{i}{\mathrm{argmax}}(Z(x{)}_i)$，这里$Z(X)\in {\mathbb{R}}^K$指代 the final (logit) layer output,，$Z(x{)}_i$是第$i$类的预测分数。（1）中的目标因此可以自然用公式表达为如下的优化问题：

$$\underset{x}{\mathrm{argmin}}\{\text{Dis}(x,x_0)+c\mathcal{L}(Z(x))\}:h(x)(2)$$

这里$\text{Dis}(\cdot ,\cdot )$指代某种距离测量方式（例如$l_2,l_1$或$l_{\infty }$范数）。$\mathcal{L}(\cdot )$is the loss function corresponding to the goal of the attack，and $c$ is a balancing parameter。对于untargeted攻击，最终目标是使得目标分类器错分类，那么loss function可以通过如下的方式进行定义：

2.3 Previous work on black-box attack

在真实世界中，我们通常无法得到白盒攻击所需信息，因此我们需要关注于黑盒攻击。对于黑盒攻击的第一次尝试是使用tranfer attack[14]，instead of攻击原始模型$f$，攻击者尝试构建一个 substitute model $\hat{f}$来模拟$f$并且使用白盒攻击方式来攻击$\hat{f}$。这种方式在[15]中进行了详细的研究调查。然而，最近的论文have shown that attacking the substitute model usually leads to much larger distortion and low success rate [10]. 因此， instead, [10] considers the score-based black-box setting, where attackers can use x to query the softmax layer output in addition to the final classification result.在这种情况下，他们可以重建loss function (3) and evaluate it as long as the objective function h(x) exists for any x. Thus a zeroth order optimization approach can be directly applied to minimize h(x). [16] further improves the query complexity of [10] by introducing two novel building blocks: (i) an adaptive random gradient estimation algorithm that balances query counts and distortion, and (ii) a well-trained autoencoder that achieves attack acceleration. [13] also solves a score-based attack problem using an evolutionary algorithm and it shows their method could be applied to hard-label black-box setting as well.

2.4 hard-label黑盒攻击的困难

在本文中，hard-label黑盒设定指 real-world ML systems only provide limited prediction results of an input query的情况。特别地，攻击者只知道模型的top-1预测标签而不是概率输出。

在这种设定下进行的攻击十分困难，在图1a中，我们展示了一个简单的三层神经网络的决策边界：

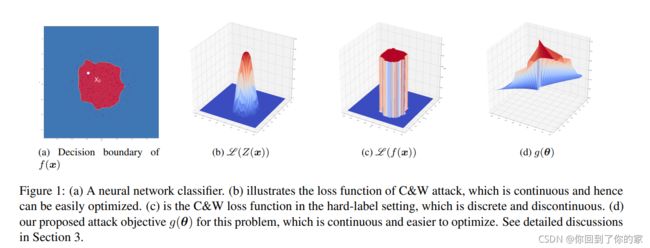
注意$\mathcal{L}(Z(x))$term is continuous as in Figure 1b because the logit layer output is real-valued functions（？）。然而，在hard-label黑盒设定下，我们仅能得到$f(\cdot )$而不是$Z(\cdot )$。 Since f(·) can only be
one-hot vector, if we plug-in f into the loss function, L (f(x)) (as shown in Figure 1c) will be discontinuous and with
discrete outputs.

最优化这个函数will require combinatorial optimization or search algorithms，which is almost impossible
to do given high dimensionality of the problem. Therefore, almost no algorithm can successfully conduct hard-label
black-box attack in the literature. The only current approach [1] is based on random-walk on the boundary. Although this
decision-based attack can find adversarial examples with comparable distortion with white-box attacks, it suffers from exponential search time, resulting in lots of queries, and lacks convergence guarantees. We show that our optimizationbased algorithm can significantly reduce the number of queries compared with decision-based attack, and has guaranteed convergence in the number of iterations (queries).

3 Algorithms

Now we will introduce a novel way to re-formulate hard-label black-box attack as another optimization problem, show
how to evaluate the function value using hard-label queries, and then apply a zeroth order optimization algorithm to
solve it

3.1 A Boundary-based Re-formulation

对于一个给定的数据样本$x_0$，真实标签$y_0$以及hard-label黑盒函数$f:{\mathbb{R}}^d\to \{1,\dots ,K\}$，我们根据攻击类型定义目标函数$g:{\mathbb{R}}^d\to \mathbb{R}$：

$$\text{Untargeted attack}:g(\theta )=\underset{\lambda >0}{\mathrm{argmin}}(f(x_0+\lambda \frac{\theta }{\Vert \theta \Vert )}\ne y_0)(4)$$

$$\text{Targeted attack (given target t)}:g(\theta )=\underset{\lambda >0}{\mathrm{argmin}}(f(x_0+\lambda \frac{\theta }{\Vert \theta \Vert })=t)(5)$$

在上面的公式中，$\theta$表示搜索方向，$g(\theta )$表示从$x_0$到最近的对抗样本之间沿$\theta$的距离。 The difference between (4) and (5) corresponds to the different definitions of “successfulness” in untargeted and targeted attack, where the former one aims to turn the prediction into any incorrect label and the later one aims to turn the prediction into the target label. 对于untargeted attack, g(θ) also corresponds to the distance to the decision boundary along the direction θ. In image problems the input domain of f is bounded, so we will add corresponding upper/lower bounds in the definition of (4) and (5).

Instead of searching for an adversarial example, we search the direction θ to minimize the distortion g(θ), which leads to the following optimization problem:

$$\underset{\theta }{\min }g(\theta )(6)$$

然后，对抗样本就可以通过$x^{\ast }=x_0+g({\theta }^{\ast })\frac{{\theta }^{\ast }}{\Vert {\theta }^{\ast }\Vert }$找到，这里${\theta }^{\ast }$是（6）中的最优解。

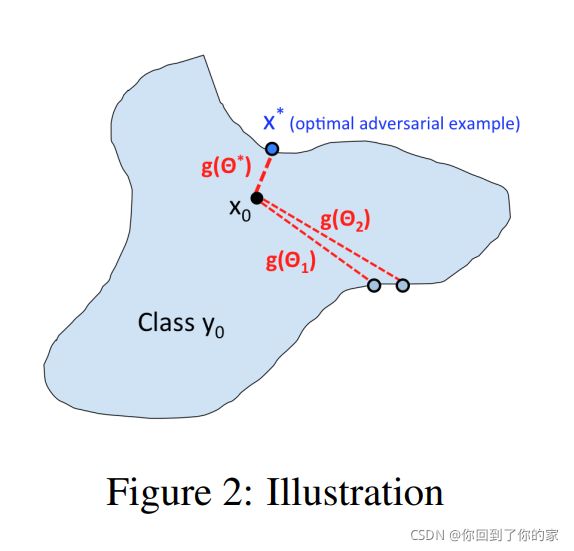
Note that unlike the C&W or PGD objective functions, which are discontinuous step functions in the hard-label setting (see Section 2), g(θ) maps input
direction to real-valued output (distance to decision boundary), which is usually
continuous—a small change of θ usually leads to a small change of g(θ), as can
be seen from Figure 2.

此外，我们给出三个定义在二位输入空间$f(x)$以及它们对应的$g(\theta )$的例子。在图3a中，我们有一个continuous classification function defined as follows

$$f(x)=\{\begin{array}{l}1,\text{if}\Vert x{\Vert }^2\ge 0.4\\ 0,\text{otherwise}\end{array}$$

在这种情况下，如图3c所示，$g(\theta )$是连续的。Moreover, in Figure 3b and Figure 1a, we show decision
boundaries generated by GBDT and neural network classifier, which are not continuous. However, as showed in Figure
3d and Figure 1d, even if the classifier function is not continuous, g(θ) is still continuous. This makes it easy to apply
zeroth order method to solve (6).

Compute $g(\theta )$ up to certain accuracy

我们无法evaluate $g$的梯度，但是我们可以使用关于原始函数$f$的hard label查询来evaluate $g$的function value。为了简化表述，我们在这里关注untargeted攻击，但是注意同样的过程也可以应用于targeted attack。

首先，我们讨论怎么在没有额外信息的情况下直接计算得到$g(\theta )$。这应用到了我们的算法的初始化步骤中。对于一个给定的normalized $\theta$，我们进行一个find-grained搜索然后进行二分搜索。在fine-grained 搜索过程中，我们查询点$\{x_0+\alpha \theta ,x_0+2\alpha \theta ,\dots \}$，依次查询知道我们找到$f(x_0+i\alpha \theta )\ne y_0$。这代表决策边界位于$[x_0+(i-1)\alpha \theta ,x_0+i\alpha \theta ]$内。我们接下来进入第二阶段然后在这个新找到的区域内进行二分搜索（和算法1的11-17行一样）。Note that there is an upper bound of the first stage if we choose θ by the direction of x − x0 with some x from another class. This procedure is used to find the initial θ0 and corresponding g(θ0) in our optimization algorithm. We omit the detailed algorithm for this part since it is similar to Algorithm 1.

Next, we discuss how to compute g(θ) when we know the solution is very close to a value v. This is used in all the
function evaluations in our optimization algorithm, since the current solution is usually close to the previous solution,
and when we estimate the gradient using (7), the queried direction will only be a small perturbation of the previous one.
In this case, we first increase or decrease v in local region to find the interval that contains boundary (e.g, f(v) = y0 and
f(v
0
) 6= y0), then conduct a binary search to find the final value of g. Our procedure for computing g value is presented
in Algorithm 1.

3.2 Zeroth Order Optimization

为了在我们仅能获取函数值而无法获取梯度的情况下解决优化问题（1），zeroth order optimization algorithms can be naturally applied。 In fact, after the reformulation, the problem can be potentially solved by any zeroth order optimization algorithm, like zeroth order gradient descent or coordinate descent (see [17] for a comprehensive survey).

Here we propose to solve (1) using Randomized Gradient-Free (RGF) method proposed in [2, 18]. In practice we found it outperforms zeroth-order coordinate descent. In each iteration, the gradient is estimated by

$$\hat{g}=\frac{g(\theta +\beta u)-g(\theta )}{\beta }\cdot u(7)$$

where u is a random Gaussian vector, and β > 0 is a smoothing parameter (we set β = 0.005 in all our experiments). The solution is then updated by θ ← θ − ηgˆ with a step size η. The procedure is summarized in Algorithm 2.

There are several implementation details when we apply this algorithm. First, for high-dimensional problems, we
found the estimation in (7) is very noisy. Therefore, instead of using one vector, we sample q vectors from Gaussian
distribution and average their estimators to get gˆ. We set q = 20 in all the experiments. The convergence proofs can be
naturally extended to this case. Second, instead of using a fixed step size (suggested in theory), we use a backtracking
line-search approach to find step size at each step. This leads to additional query counts, but makes the algorithm more
stable and eliminates the need to hand-tuning the step size.

3.3 Theoretical Analysis

If g(θ) can be computed exactly, it has been proved in [2] that RGF in Algorithm 2 requires at most O(
d
δ
2 ) iterations
to converge to a point with k∇g(θ)k
2 ≤ δ
2
. However, in our algorithm the function value g(θ) cannot be computed
exactly; instead, we compute it up to -precision, and this precision can be controlled by binary threshold in Algorithm 1.
We thus extend the proof in [2] to include the case of approximate function value evaluation, as described in the following
theorem.
Theorem 1 In Algorithm 2, suppose g has Lipschitz-continuous gradient with constant L1(g). If the error of function
value evaluation is controlled by ∼ O(βδ2
) and β ≤ O(
δ
dL1(g)
), then in order to obtain 1
N+1
P
N
k=0
EUk
(k∇g(θk)k
2
) ≤
δ
2
, the total number of iterations is at most O(
d
δ
2 ).
Detailed proofs can be found in the appendix. Note that the binary search procedure could obtain the desired function
value precision in O(log δ) steps. By using the same idea with Theorem 1 and following the proof in [2], we could also
achieve O(
d
2
δ
3 ) complexity when g(θ) is non-smooth but Lipschitz continuous.