解读数学问题自动求解领域的一篇论文A Goal-Driven Tree-Structured Neural Model for Math Word Problems以及论文的代码

论文链接
代码链接

模型大概框架:

这篇论文的思想就是：传统的seq2seq模型是序列式的从左到右生成表达式，缺少一种“目标驱动”机制，而这种目标驱动机制在人类解题过程中是常见的。
例如这么一道题：

小明正在将他的饼干装进包中，一个包里面要装6块饼干。如果他有23块巧克力饼干，25块曲奇饼干，那么他需要几个包？

对于这个问题，我们在解答的时候，首先看出来问题的目标是计算需要几个包，针对这个目标，我们提取相关的信息：一个包里面装6个饼干;有23块巧克力饼干;有25块曲奇饼干。于是乎我们知道，要想得到最终目标需要几个包，我们需要将它分解为两个子目标:
(1)一共有多少块饼干;(2)一个包里面可以装几块饼干
而且最终目标要通过(1)/(2)得到，也就是子目标(1)的结果除以子目标(2)的结果

• 针对第一个子目标，还需要继续分解成子目标：(11)有23块巧克力饼干;(22)有25块曲奇饼干
  而且第一个字目标的结果要通过(11)+(22)得到。两个子子目标(11)和(22)，不用分解了，我们已经可以直接从题目文本中提取出目标的结果，分别是23和25。
• 针对第二个子目标，同样可以直接从文本中提取目标的结果，也就是6.

所以最终的表达式是(23+25)/6

所以按照上述的思想，模型的流程如下：

1. 首先初始化一个根目标向量，代表整个问题的最终目标。对应上面例子中的需要几个包
2. 根据根目标向量，获取相关的上下文信息。比如对应上面例子中的一个包里面装6个饼干;有23块巧克力饼干;有25块曲奇饼干。
3. 接下来利用上下文信息以及根目标向量预测根目标位置对应的token。比如根据上面这个例子，我们应该预测出来对应的token是除号(话说除号怎么用键盘打出来呢)，这里用/表示除号。然后我们发现预测出来的token是运算符/，而不是数字，那么就说明它一定要分解成两个子目标。
4. 假设正确的分解成了两个子目标：(1)一共有多少块饼干;(2)一个包里面可以装几块饼干。
5. 然后我们预测第一个子目标的token，发现是运算符+，那么接着分解…
6. 按照这个思想流程，我们也就从上到下的构建了论文中图１所示的表达式树

模型处理细节:

数据处理:

• 定义$n_p$是一个有序的列表，它存储的是对应的问题文本中出现的数字，而且按照数字出现的顺序有序存储。对应上面的例子就是$n_p$=[6,23,25]。
• 问题文本中出现的数字要同意被替换成NUM，因为我们并不关系数值具体是多少，我们要的是推理出来表达式。对应上面的例子就是小明正在将他的饼干装进包中，一个包里面要装NUM块饼干。如果他有NUM块巧克力饼干，NUM块曲奇饼干，那么他需要几个包？
• 解码端，也就是输出的词汇空间定义为$V^{dec}$，它包含三个部分，第一个就是问题文本中出现的数字$n_P$，第二个是运算符集合，一般就是加减乘除。第三个是常数集合，比如$\pi$，因为有的问题问的是面积或者周长，但是问题中不会出现$\pi$，而表达式却会出现$\pi r^2$这种。

模型描述:

模型的思想就是对问题文本中出现的数字，建立这些数字之间的树形结构关系。

树中的每一个节点有三个主要成分：这个节点的目标向量$\mathbf{q}$；这个节点所预测的token $\hat{y}$；这个节点的子目标的嵌入向量$\mathbf{t}$(也就是这个节点的子树的嵌入)

下面我们一步一步的来看：

1. 首先要做的显然是把整个question文本送入一个BiGRU，对应论文中的公式(1)(2)(3)
2. 当我们读完了问题之后，怎么定义最终目标，也就是根节点的向量$\mathbf{q}$呢，看论文的公式(4)，显然是前向GRU的最后一个时刻的hidden state和反向GRU的最后一个hidden state两者相加，得到${\mathbf{q}}_0$。对应上面的例子，这个${\mathbf{q}}_0$编码语义就是需要几个包。
3. 接下来的步骤就是根据目标向量$\mathbf{q}$去获得相关的上下文信息，也就是拿目标向量$\mathbf{q}$和整个问题文本question做一次注意力的运算，提取相关的信息，对应公式(6)。比如在根节点的目标向量下，提取的信息应该是：一个包里面装6个饼干;有23块巧克力饼干;有25块曲奇饼干。
4. 我们现在已经得到了论文中的$\mathbf{q},\mathbf{c}$，这两个都是一个向量，长度是dim。现在来看公式(5)，它是decoder端，也就是输出端的词汇空间中每一个词汇对应的向量表示，其中${\text{M}}_{op}$和${\text{M}}_{con}$代表的是两个专门的查找表，也就是嵌入矩阵。${\text{M}}_{op}$用来查找运算符加减乘除对应的embedding。${\text{M}}_{con}$用来查找常数对应的embedding，比如$\pi$这种常数。这两个嵌入矩阵都是预先初始化然后随着模型训练更新向量值的，它们对于所有问题的预测都适用。但是$h_{loc}^P$不一样，它是该问题文本中数字那个位置对应的embedding，不同的问题显然该值不同。比如上面的例子，此时$\mathbf{e}(y|P)$的形状我们可以认为是(8,512)，其中512是向量维度，8=4+1+3，其中4表示加减乘除，1表示常数$\pi$，３表示那三个数字:6,23,25
5. 现在我们已经获得了$\mathbf{q},\mathbf{c},\mathbf{e}(y|P)$，根据公式(7)我们就得到了$s(y|q,c,P)$，它是长度为8的向量，每一个值表示预测的token的分数，然后softmax，也就是论文的公式8，我们就得到了预测每一个token的概率。比如[0.1,0.15,0.13,0.37,0.2,0.1,0.1,…]，这表示预测加号的概率是0.1，预测减号的概率是0.15，预测除号的概率是0.37。取最大的值，对应公式(9)，所以我们现在预测了当前节点应该是除号。
6. 既然预测了token是除号，那么显然要继续分解成子目标。：(1)一共有多少块饼干;(2)一个包里面可以装几块饼干。
7. 我们来看左边的子目标(左边的节点)：一共有多少块饼干，这个子目标对应的目标向量定义为${\mathbf{q}}_l$，计算方式为公式(10)。我们可以看到它是利用了根节点的目标向量$\mathbf{q}$;$\mathbf{q}$和question做注意力得到的上下文信息向量$\mathbf{c}$;还有根节点对应的预测的token $\hat{y}$的向量表示$\mathbf{e}(\hat{y}|P)$。利用这三个向量计算得到了${\mathbf{q}}_l$，此时${\mathbf{q}}_l$表征的语义就是一共有多少块饼干
8. 得到了${\mathbf{q}}_l$之后，我们就要预测这个节点对应的token. 计算过程和前面一样。第一步：利用${\mathbf{q}}_l$和question做注意力计算，得到上下文信息向量$\mathbf{c}$（按照我们的这个例子，此时的$\mathbf{c}$应该蕴含着{有23块巧克力饼干;有25块曲奇饼干}这样的语义信息）。第二步：利用${\mathbf{q}}_l$和$\mathbf{c}$以及$\mathbf{e}(y|P)$按照公式(7),(8)预测这个token $\hat{y}$。假如预测之后是加号+，那么要继续分解成子目标:有23块巧克力饼干;有25块曲奇饼干
9. 同样的道理，同样的步骤。假如我们已经计算得到了左边节点的目标向量${\mathbf{q}}_l$，它表征的语义是有23块巧克力饼干。现在到了预测token这步，对于左边的节点，我们发现预测的token是23，这是数字，不用继续分解了。还记得之前说过，每一个节点有三个组成成分：(1)该节点的目标向量；(2)该节点预测的token；(3)该节点的子树向量$\mathbf{t}$。
10. 对于叶子节点来说，子树向量$\mathbf{t}$就是该节点的token的向量，见公式(12):{ if $\hat{y}\in n_P\cup V_{con}$，那么$\mathbf{t}=\mathbf{e}(\hat{y}|P)$}。见论文的图２中圈3和圈5两个编号，所以我们就得到了23这个节点的完整信息，也就是这三个组成部分。
11. 对于25这个节点，需要注意的是，它是右子树，它的目标向量的生成方式要考虑左子树。步骤:　第一步，利用加号这个节点的目标向量$\mathbf{q}$，$\mathbf{q}$和question做注意力得到的$\mathbf{c}$，以及兄弟节点23的向量，来计算25这个节点的目标向量。然后预测token，假如是25，发现是数字，不用再分解了，对应的子树向量就是本身的向量。具体的见公式(11)和图２的圈4以及圈5
12. 现在回溯到加号+这个节点，它的子树向量的计算方式见公式(12)和公式(13)，无非是将23和25两个向量按照公式(13)的计算方式结合。见图２的圈6
13. 至此，我们计算完了根节点的第一个子目标，然后是计算根节点的第二个子目标: 第一步，利用根节点的目标向量$\mathbf{q}$；$\mathbf{q}$和question做注意力得到的$\mathbf{c}$；以及兄弟节点加号的子树向量。根据公式11计算得到了目标向量${\mathbf{q}}_r$，然后预测token，假如是6，发现是数字，不再分解，对应的子树向量就是数字6的向量。

整个表达式树就建立完成了，只需要遍历树中每一个节点对应的token，就得到了表达式。

代码部分解读：

首先我们从2万多个问题中选出来10个问题，这10个问题是具有代表性的，比如出现了3.14，出现了重复数字等:

data=[{'id': '0', 'original_text': '镇海雅乐学校二年级的小朋友到一条小路的一边植树．小朋友们每隔2米种一棵树（马路两头都种了树），最后发现一共种了11棵，这条小路长多少米．', 'segmented_text': '镇海 雅乐 学校 二年级 的 小朋友 到 一条 小路 的 一边 植树 ． 小朋友 们 每隔 2 米 种 一棵树 （ 马路 两头 都 种 了 树 ） ， 最后 发现 一共 种 了 11 棵 ， 这 条 小路 长 多少 米 ．', 'equation': 'x=(11-1)*2', 'ans': '20'},
         {'id': '1', 'original_text': '某工厂积极开展植树活动．第一车间45人，第二车间42人，平均每人植树8棵．两个车间一共植树多少棵？', 'segmented_text': '某 工厂 积极开展 植树 活动 ． 第一 车间 45 人 ， 第 二 车间 42 人 ， 平均 每人 植树 8 棵 ． 两个 车间 一共 植树 多少 棵 ？', 'equation': 'x=45*8+42*8', 'ans': '696'}, 
         {'id': '2', 'original_text': '一个工程队挖土，第一天挖了316方，从第二天开始每天都挖230方，连续挖了6天，这个工程队一周共挖土多少方？', 'segmented_text': '一 个 工程队 挖土 ， 第一天 挖 了 316 方 ， 从 第 二 天 开始 每天 都 挖 230 方 ， 连续 挖 了 6 天 ， 这个 工程队 一周 共 挖土 多少 方 ？', 'equation': 'x=316+230*(6-1)', 'ans': '1466'}, 
         {'id': '3', 'original_text': '小明看一本故事书，第一天看了全书的(1/6)，第二天看了24页，第3天看的页数是前两天看的总数的150%，这时还有全书的(1/4)没有看，那么这本书一共多少页．', 'segmented_text': '小 明 看 一本 故事书 ， 第一天 看 了 全书 的 (1/6) ， 第 二 天 看 了 24 页 ， 第 3 天 看 的 页数 是 前两天 看 的 总数 的 150% ， 这时 还有 全书 的 (1/4) 没有 看 ， 那么 这 本书 一共 多少 页 ．', 'equation': 'x=(24+24*150%)/(1-(1/6)-(1/6)*150%-(1/4))', 'ans': '180'}, 
         {'id': '4', 'original_text': '小明看一本书，第一天看了全书的(1/5)，第二天比第一天多看14页，剩下的25页第3天看完，这本书共有多少页？', 'segmented_text': '小 明 看 一 本书 ， 第一天 看 了 全书 的 (1/5) ， 第 二 天 比 第一天 多 看 14 页 ， 剩下 的 25 页 第 3 天 看 完 ， 这 本书 共有 多少 页 ？', 'equation': 'x=(25+14)/(1-(1/5)-(1/5))', 'ans': '65'}, 
         {'id': '5', 'original_text': '小芳家5月份用水量是16.5吨，每吨水的价格是2.1元，小芳家一共有5口人，平均每人应交多少水费？', 'segmented_text': '小 芳 家 5 月份 用水量 是 16.5 吨 ， 每吨 水 的 价格 是 2.1 元 ， 小 芳 家 一共 有 5 口 人 ， 平均 每人 应交 多少 水费 ？', 'equation': 'x=16.5*2.1/5', 'ans': '6.93'}, 
         {'id': '6', 'original_text': '比一个数多12%的数是112，这个数=？', 'segmented_text': '比 一个 数多 12% 的 数 是 112 ， 这个 数 = ？', 'equation': 'x=112/(1+12%)', 'ans': '100'}, 
         {'id': '7', 'original_text': '商店里有梨390千克，比苹果少40%，商店里有苹果多少千克？', 'segmented_text': '商店 里 有 梨 390 千克 ， 比 苹果 少 40% ， 商店 里 有 苹果 多少 千克 ？', 'equation': 'x=390/(1-40%)', 'ans': '650'},
         {'id': '8', 'original_text': '早晨教室里有36名学生，其中女生占教室里总人数的(5/9)，后来又来了几名女生，这时女生占教室里总人数的(11/19)，后来又来了几名女生？', 'segmented_text': '早晨 教室 里 有 36 名 学生 ， 其中 女生 占 教室 里 总 人数 的 (5/9) ， 后来 又 来 了 几名 女生 ， 这时 女生 占 教室 里 总 人数 的 (11/19) ， 后来 又 来 了 几名 女生 ？', 'equation': 'x=36*(1-(5/9))/(1-(11/19))-36', 'ans': '2'},
         {'id': '9', 'original_text': '一个车轮的外直径是4dm，它滚动10距离=多少dm．', 'segmented_text': '一 个 车轮 的 外 直径 是 4dm ， 它 滚动 10 距离 = 多少 dm ．', 'equation': 'x=3.14*4*10', 'ans': '125.6'}]

我们就用这10个问题来看下面的代码:
整个代码的主函数是run_seq2seq.py

前期准备

import random
import json
import copy
import re
import torch
import torch.nn as nn
import math
from copy import deepcopy
data=[{'id': '0', 'original_text': '镇海雅乐学校二年级的小朋友到一条小路的一边植树．小朋友们每隔2米种一棵树（马路两头都种了树），最后发现一共种了11棵，这条小路长多少米．', 'segmented_text': '镇海 雅乐 学校 二年级 的 小朋友 到 一条 小路 的 一边 植树 ． 小朋友 们 每隔 2 米 种 一棵树 （ 马路 两头 都 种 了 树 ） ， 最后 发现 一共 种 了 11 棵 ， 这 条 小路 长 多少 米 ．', 'equation': 'x=(11-1)*2', 'ans': '20'},
         {'id': '1', 'original_text': '某工厂积极开展植树活动．第一车间45人，第二车间42人，平均每人植树8棵．两个车间一共植树多少棵？', 'segmented_text': '某 工厂 积极开展 植树 活动 ． 第一 车间 45 人 ， 第 二 车间 42 人 ， 平均 每人 植树 8 棵 ． 两个 车间 一共 植树 多少 棵 ？', 'equation': 'x=45*8+42*8', 'ans': '696'}, 
         {'id': '2', 'original_text': '一个工程队挖土，第一天挖了316方，从第二天开始每天都挖230方，连续挖了6天，这个工程队一周共挖土多少方？', 'segmented_text': '一 个 工程队 挖土 ， 第一天 挖 了 316 方 ， 从 第 二 天 开始 每天 都 挖 230 方 ， 连续 挖 了 6 天 ， 这个 工程队 一周 共 挖土 多少 方 ？', 'equation': 'x=316+230*(6-1)', 'ans': '1466'}, 
         {'id': '3', 'original_text': '小明看一本故事书，第一天看了全书的(1/6)，第二天看了24页，第3天看的页数是前两天看的总数的150%，这时还有全书的(1/4)没有看，那么这本书一共多少页．', 'segmented_text': '小 明 看 一本 故事书 ， 第一天 看 了 全书 的 (1/6) ， 第 二 天 看 了 24 页 ， 第 3 天 看 的 页数 是 前两天 看 的 总数 的 150% ， 这时 还有 全书 的 (1/4) 没有 看 ， 那么 这 本书 一共 多少 页 ．', 'equation': 'x=(24+24*150%)/(1-(1/6)-(1/6)*150%-(1/4))', 'ans': '180'}, 
         {'id': '4', 'original_text': '小明看一本书，第一天看了全书的(1/5)，第二天比第一天多看14页，剩下的25页第3天看完，这本书共有多少页？', 'segmented_text': '小 明 看 一 本书 ， 第一天 看 了 全书 的 (1/5) ， 第 二 天 比 第一天 多 看 14 页 ， 剩下 的 25 页 第 3 天 看 完 ， 这 本书 共有 多少 页 ？', 'equation': 'x=(25+14)/(1-(1/5)-(1/5))', 'ans': '65'}, 
         {'id': '5', 'original_text': '小芳家5月份用水量是16.5吨，每吨水的价格是2.1元，小芳家一共有5口人，平均每人应交多少水费？', 'segmented_text': '小 芳 家 5 月份 用水量 是 16.5 吨 ， 每吨 水 的 价格 是 2.1 元 ， 小 芳 家 一共 有 5 口 人 ， 平均 每人 应交 多少 水费 ？', 'equation': 'x=16.5*2.1/5', 'ans': '6.93'}, 
         {'id': '6', 'original_text': '比一个数多12%的数是112，这个数=？', 'segmented_text': '比 一个 数多 12% 的 数 是 112 ， 这个 数 = ？', 'equation': 'x=112/(1+12%)', 'ans': '100'}, 
         {'id': '7', 'original_text': '商店里有梨390千克，比苹果少40%，商店里有苹果多少千克？', 'segmented_text': '商店 里 有 梨 390 千克 ， 比 苹果 少 40% ， 商店 里 有 苹果 多少 千克 ？', 'equation': 'x=390/(1-40%)', 'ans': '650'},
         {'id': '8', 'original_text': '早晨教室里有36名学生，其中女生占教室里总人数的(5/9)，后来又来了几名女生，这时女生占教室里总人数的(11/19)，后来又来了几名女生？', 'segmented_text': '早晨 教室 里 有 36 名 学生 ， 其中 女生 占 教室 里 总 人数 的 (5/9) ， 后来 又 来 了 几名 女生 ， 这时 女生 占 教室 里 总 人数 的 (11/19) ， 后来 又 来 了 几名 女生 ？', 'equation': 'x=36*(1-(5/9))/(1-(11/19))-36', 'ans': '2'},
         {'id': '9', 'original_text': '一个车轮的外直径是4dm，它滚动10距离=多少dm．', 'segmented_text': '一 个 车轮 的 外 直径 是 4dm ， 它 滚动 10 距离 = 多少 dm ．', 'equation': 'x=3.14*4*10', 'ans': '125.6'}]

def print_data(data):
    for i in data:
        print(i)
        print()
        
print_data(data)

修改transfer_num

def transfer_num(data):  # transfer num into "NUM"
    print("Transfer numbers...")
    pattern = re.compile("\d*\(\d+/\d+\)\d*|\d+\.\d+%?|\d+%?")
    pairs = []
    generate_nums = []#用来记录那些在表达式中出现，但是不在问题中出现的数字
    generate_nums_dict = {}
    copy_nums = 0
    for d in data:
        nums = []
        input_seq = []
        seg = d["segmented_text"].strip().split(" ")#获得了问题文本的列表表示
        equations = d["equation"][2:]

        for s in seg:
            pos = re.search(pattern, s)
            if pos and pos.start() == 0:
                nums.append(s[pos.start(): pos.end()])
                input_seq.append("NUM")#input_seq的目的是将问题中所有的数字转成NUM
                if pos.end() < len(s):
                    input_seq.append(s[pos.end():])
            else:
                input_seq.append(s)
        #nums记录的就是问题中出现的所有数字
        if copy_nums < len(nums):
            copy_nums = len(nums)
        #copy_nums用来得到数据集中所有问题中出现数字次数最多的对应的次数

        nums_fraction = []

        for num in nums:
            if re.search("\d*\(\d+/\d+\)\d*", num):
                nums_fraction.append(num)
        nums_fraction = sorted(nums_fraction, key=lambda x: len(x), reverse=True)
        #num_fraction用来记录问题中出现(1/2)这种利用括号括起来的分数形式的数字
        def seg_and_tag(st):  # seg the equaticopy_numson and tag the num
            res = []
            for n in nums_fraction:
                if n in st:
                    p_start = st.find(n)
                    p_end = p_start + len(n)
                    if p_start > 0:
                        res += seg_and_tag(st[:p_start])
                    if nums.count(n) == 1:
                        res.append("N"+str(nums.index(n)))
                    else:
                        res.append(n)
                    if p_end < len(st):
                        res += seg_and_tag(st[p_end:])
                    return res
            pos_st = re.search("\d+\.\d+%?|\d+%?", st)
            if pos_st:
                p_start = pos_st.start()
                p_end = pos_st.end()
                if p_start > 0:
                    res += seg_and_tag(st[:p_start])
                st_num = st[p_start:p_end]
                if nums.count(st_num) == 1:
                    res.append("N"+str(nums.index(st_num)))
                else:
                    res.append(st_num)#这行特别要注意，也就是说，如果nums中发现这个数字出现的次数不止一次
                    #那么我们就在输出的表达式中直接填上这个数字，而不是利用N+数字的位置代替。
                if p_end < len(st):
                    res += seg_and_tag(st[p_end:])
                return res
            for ss in st:
                res.append(ss)
            return res

        out_seq = seg_and_tag(equations)
        print("question : ",d['original_text'])
        print('expression : ',d['equation'])
        print('input seq : ',input_seq)
        print('output seq : ',out_seq)
        print("问题中是否出现了括号括起来的分数形式的数字　: ",nums_fraction)
        for s in out_seq:  # tag the num which is generated
            if s[0].isdigit() and s not in generate_nums and s not in nums:
                generate_nums.append(s)
                generate_nums_dict[s] = 0
            if s in generate_nums and s not in nums:
                generate_nums_dict[s] = generate_nums_dict[s] + 1

        num_pos = []
        for i, j in enumerate(input_seq):
            if j == "NUM":
                num_pos.append(i)
        assert len(nums) == len(num_pos)
        # pairs.append((input_seq, out_seq, nums, num_pos, d["ans"]))
        print('问题中出现的数字 : ',nums)
        print("数字在问题中的位置　: ",num_pos)
        print('-'*100)
        pairs.append((input_seq, out_seq, nums, num_pos))

    temp_g = []
    for g in generate_nums:
        if generate_nums_dict[g] >= 1:
            temp_g.append(g)
    return pairs, temp_g, copy_nums

pairs, generate_nums, copy_nums = transfer_num(data)
print_data(pairs)

print(generate_nums)
print(copy_nums)

打印的结果如下：

也就是说，1和3.14这两个数字是常数，它们不在问题中出现，但是在equation中出现。对应的就是论文中的$V_{con}$

copy_nums=5，含义是这10个问题中出现数字次数最多的那个问题中，出现了5个数字

将中缀表达式转成前缀

temp_pairs = []
for p in pairs:
    temp_pairs.append((p[0], from_infix_to_prefix(p[1]), p[2], p[3]))
pairs = temp_pairs
print_data(pairs)

特别要注意一种情况，就是问题中出现了重复的数字：

for i,pair in enumerate(pairs):
    output_seq=pair[1]
    for each_ in output_seq:
        if each_.isdigit() and each_ not in ['1','3.14']:
            print("当前的这个问题中出现了两个重复数字")
            print(data[i])
            print(pair)

此时表达式的输出是[’/’, ‘*’, ‘N1’, ‘N2’, ‘5’]。这是要特别注意的

修改prepare_data

def prepare_data(pairs_trained, pairs_tested, trim_min_count, generate_nums, copy_nums, tree=False):
    input_lang = Lang()
    output_lang = Lang()
    train_pairs = []
    test_pairs = []

    print("Indexing words...")
    for pair in pairs_trained:
        input_lang.add_sen_to_vocab(pair[0])#构造encoder端的词汇
        output_lang.add_sen_to_vocab(pair[1])#构造decoder端的词汇

    input_lang.build_input_lang(trim_min_count)#构造encoder端的word2id
    if tree:
        output_lang.build_output_lang_for_tree(generate_nums, copy_nums)#构造decoder端的word2id
    else:
        output_lang.build_output_lang(generate_nums, copy_nums)

    for pair in pairs_trained:
        num_stack = []
        for word in pair[1]:
            #pair[1]指的是输出的前缀表达式self.index2word + generate_num + ["N" + str(i) for i in range(copy_nums)] + ["UNK"]
            temp_num = []
            flag_not = True
            if word not in output_lang.index2word:
                #word不在decoder端的word2id的唯一可能性就是上面提到的，出现了重复数字
                flag_not = False
                for i, j in enumerate(pair[2]):
                    if j == word:
                        temp_num.append(i)

            if not flag_not and len(temp_num) != 0:
                num_stack.append(temp_num)
            if not flag_not and len(temp_num) == 0:
                num_stack.append([_ for _ in range(len(pair[2]))])

        num_stack.reverse()#num_stack记录的就是重复数字在nums中出现的位置，别忘了nums记录的是问题中所有出现的数字
        input_cell = indexes_from_sentence(input_lang, pair[0])
        output_cell = indexes_from_sentence(output_lang, pair[1], tree)
        train_pairs.append((input_cell, len(input_cell), output_cell, len(output_cell),
                            pair[2], pair[3], num_stack))
    print('Indexed %d words in input language, %d words in output' % (input_lang.n_words, output_lang.n_words))
    print('Number of training data %d' % (len(train_pairs)))
    for pair in pairs_tested:
        num_stack = []
        for word in pair[1]:
            temp_num = []
            flag_not = True
            if word not in output_lang.index2word:
                flag_not = False
                for i, j in enumerate(pair[2]):
                    if j == word:
                        temp_num.append(i)

            if not flag_not and len(temp_num) != 0:
                num_stack.append(temp_num)
            if not flag_not and len(temp_num) == 0:
                num_stack.append([_ for _ in range(len(pair[2]))])

        num_stack.reverse()
        input_cell = indexes_from_sentence(input_lang, pair[0])#sentence转换为id
        output_cell = indexes_from_sentence(output_lang, pair[1], tree)#equation转换为id,注意
        #由于重复数字不在output_lang.word2index中出现，所以带有数字的表达式中，数字是被替换为UNK的
        test_pairs.append((input_cell, len(input_cell), output_cell, len(output_cell),
                           pair[2], pair[3], num_stack))
    print('Number of testind data %d' % (len(test_pairs)))        # train_pairs.append((input_cell, len(input_cell), output_cell, len(output_cell),
        #                     pair[2], pair[3], num_stack, pair[4]))
    return input_lang, output_lang, train_pairs, test_pairs

pairs_trained=pairs
pairs_tested=pairs
input_lang, output_lang, train_pairs, test_pairs = prepare_data(pairs_trained, pairs_tested, 0, generate_nums,
                                                                    copy_nums, tree=True)

我们打印几个结果

上图就是encoder端的词典和decoder端的词典

for i in range(len(train_pairs)):
    original_example=data[i]
    pair=pairs[i]
    train_example=train_pairs[i]
    #我们随机打印两个样本
    if i==0 or i==4:
        print(original_example)
        print(pair)
        print(train_example)
        print(output_lang.word2index)#对照着decoder端的word2id来看train_example中的输出表达式
        print('-'*100)
    output_seq=pair[1]#我们重点关注出现了重复数字的样本
    for each_ in output_seq:
        if each_.isdigit() and each_ not in ['1','3.14']:
            print("这个问题中出现了两个重复数字，所以对应的train_example中的输出表达式一定有UNK")
            print(original_example)
            print(pair)
            print(train_example)
            print('-'*100)   

执行上面的代码打印出来的结果帮助我们理解数据的构造形式：

我们可以观察得到，输入给模型的训练数据train_example有七个元素：

1. 第一个元素就是问题文本对应的id，文本中的数字都被替换成了NUM，对应的id是1
2. 第二个元素就是问题文本的长度
3. 第三个元素是问题对应的表达式对应的id，(问题的表达式已经将原来表达式中的数字全部替换为Ni(重复数字例外)，i指的是这个数字在nums中出现的位置)，需要注意的是，如果问题中出现了重复数字，那么对应的表达式中会保留原来的数字，这就导致decoder端的word2id找不到这个数字，就会出现UNK，比如我们上面的那个例子，对应的表达式的id就是[3, 0, 7, 8, 11]，显然11对应的就是UNK
4. 第四个元素就是表达式的长度
5. 第五个元素是nums，也就是问题中出现的所有数字
6. 第六个元素是nums_pos，也就是这所有元素在问题中出现的位置
7. 第七个元素注意一下,它记录的是问题中重复数字在nums中的位置，没有重复数字出现的问题对应的就是空列表

重新设置参数以及构造各个模块

batch_size = 2
embedding_size = 5
hidden_size = 6
n_epochs = 80
learning_rate = 1e-3
weight_decay = 1e-5
beam_size = 5
n_layers = 2

encoder = EncoderSeq(input_size=input_lang.n_words, embedding_size=embedding_size, hidden_size=hidden_size,
                     n_layers=n_layers)
predict = Prediction(hidden_size=hidden_size, op_nums=output_lang.n_words - copy_nums - 1 - len(generate_nums),
                     input_size=len(generate_nums))
generate = GenerateNode(hidden_size=hidden_size, op_nums=output_lang.n_words - copy_nums - 1 - len(generate_nums),
                        embedding_size=embedding_size)
merge = Merge(hidden_size=hidden_size, embedding_size=embedding_size)

encoder_optimizer = torch.optim.Adam(encoder.parameters(), lr=learning_rate, weight_decay=weight_decay)
predict_optimizer = torch.optim.Adam(predict.parameters(), lr=learning_rate, weight_decay=weight_decay)
generate_optimizer = torch.optim.Adam(generate.parameters(), lr=learning_rate, weight_decay=weight_decay)
merge_optimizer = torch.optim.Adam(merge.parameters(), lr=learning_rate, weight_decay=weight_decay)
encoder_scheduler = torch.optim.lr_scheduler.StepLR(encoder_optimizer, step_size=20, gamma=0.5)
predict_scheduler = torch.optim.lr_scheduler.StepLR(predict_optimizer, step_size=20, gamma=0.5)
generate_scheduler = torch.optim.lr_scheduler.StepLR(generate_optimizer, step_size=20, gamma=0.5)
merge_scheduler = torch.optim.lr_scheduler.StepLR(merge_optimizer, step_size=20, gamma=0.5)

修改prepare_train_batch

def pad_seq(seq, seq_len, max_length):
    seq += [PAD_token for _ in range(max_length - seq_len)]
    return seq
def prepare_train_batch(pairs_to_batch, batch_size,original_data,original_pair):
    pairs = copy.deepcopy(pairs_to_batch)
    datas=copy.deepcopy(original_data)
    orig_pairs=copy.deepcopy(original_pair)
    #original_data和original_pair是我们一会为了打印结果用的，目的是帮助我们输入数据的形式
    
    #random.shuffle(pairs)  # 去掉shuffle，不打乱
    pos = 0
    input_lengths = []
    output_lengths = []
    nums_batches = []
    batches = []
    input_batches = []
    output_batches = []
    num_stack_batches = []  # save the num stack which
    num_pos_batches = []
    num_size_batches = []
    batches_datas=[]
    batches_origianl_pairs=[]
    while pos + batch_size < len(pairs):
        batches.append(pairs[pos:pos+batch_size])
        batches_datas.append(datas[pos:pos+batch_size])
        batches_origianl_pairs.append(orig_pairs[pos:pos+batch_size])
        pos += batch_size
    batches.append(pairs[pos:])
    
    batches_datas.append(datas[pos:])
    batches_origianl_pairs.append(orig_pairs[pos:])

    for batch in batches:
        batch = sorted(batch, key=lambda tp: tp[1], reverse=True)
        input_length = []
        output_length = []
        for _, i, _, j, _, _, _ in batch:
            input_length.append(i)
            output_length.append(j)
        input_lengths.append(input_length)
        output_lengths.append(output_length)
        input_len_max = input_length[0]
        output_len_max = max(output_length)
        input_batch = []
        output_batch = []
        num_batch = []
        num_stack_batch = []
        num_pos_batch = []
        num_size_batch = []
        for i, li, j, lj, num, num_pos, num_stack in batch:
            num_batch.append(len(num))
            input_batch.append(pad_seq(i, li, input_len_max))
            output_batch.append(pad_seq(j, lj, output_len_max))
            num_stack_batch.append(num_stack)
            num_pos_batch.append(num_pos)
            num_size_batch.append(len(num_pos))
        input_batches.append(input_batch)
        nums_batches.append(num_batch)
        output_batches.append(output_batch)
        num_stack_batches.append(num_stack_batch)
        num_pos_batches.append(num_pos_batch)
        num_size_batches.append(num_size_batch)
    return input_batches, input_lengths, output_batches, output_lengths, nums_batches, num_stack_batches, num_pos_batches, num_size_batches,batches_datas,batches_origianl_pairs




input_batches, input_lengths, output_batches, output_lengths, nums_batches, num_stack_batches, num_pos_batches, num_size_batches, batches_datas,batches_original_pairs = prepare_train_batch(train_pairs, batch_size,
                                                                                                                                                                                    original_data=data,original_pair=pairs)

打印一下所有batch内的数据，帮助我们理解数据的形式:

for idx in range(len(pairs_trained)//batch_size):
    print(idx)
    input_batch=input_batches[idx]
    input_length=input_lengths[idx]
    target_batch=output_batches[idx]
    target_length=output_lengths[idx]
    num_stack_batch=num_stack_batches[idx]
    num_size_batch=num_size_batches[idx]
    num_pos=num_pos_batches[idx]
    nums_batch=nums_batches[idx]
    batch_datas=batches_datas[idx]
    batch_orig_pairs=batches_original_pairs[idx]
    print("一个mini batch内的样本如下　：　")
    for i in range(batch_size):
        print("对应的data : ",batch_datas[i])
        print("对应的pair : ",batch_orig_pairs[i])
        print("question text ids : ",input_batch[i])
        print("length of question text : ",input_length[i])
        print("expression ids : ",target_batch[i])
        print("length of expression : ",target_length[i])
        print("all numbers appear in question : ",nums_batch[i])
        print("是否出现了重复的数字，重复数字在nums中出现的下标 : ",num_stack_batch[i])
        print("number of numbers in this question : ",num_size_batch[i])
        print("position of each number in this question",num_pos[i])
        print()
    print('-'*100)

仔细看看打印出来的数据：
一共有10个样本，分成了5个batch。一个batch里面有两条数据，其中的input_seq和output_seq已经pad过了。而且是根据当前batch里面最长的为准。

我们随便打印其中的某个batch:

将数据送入模型中

现在我们已经了解了数据的形式，接下来就是论文源码中的这一行：

loss = train_tree(
    input_batches[idx], input_lengths[idx], output_batches[idx], output_lengths[idx],
    num_stack_batches[idx], num_size_batches[idx], generate_num_ids, encoder, predict, generate, merge,
    encoder_optimizer, predict_optimizer, generate_optimizer, merge_optimizer, output_lang, num_pos_batches[idx])

所以我们现在进入train_tree这个函数一探究竟
我们一行一行的执行train_tree里面的每一行代码

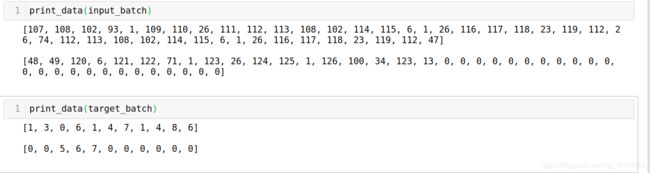
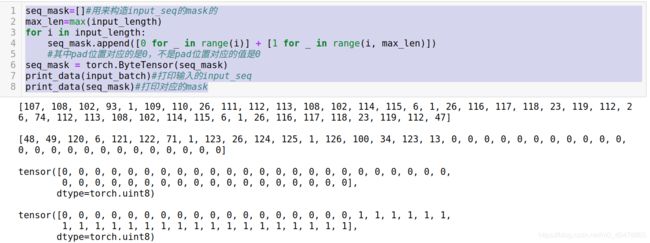
构造输入序列的mask

seq_mask=[]#用来构造input_seq的mask的
max_len=max(input_length)
for i in input_length:
    seq_mask.append([0 for _ in range(i)] + [1 for _ in range(i, max_len)])
    #其中pad位置对应的是0，不是pad位置对应的值是0
seq_mask = torch.ByteTensor(seq_mask)
print_data(input_batch)#打印输入的input_seq
print_data(seq_mask)#打印对应的mask

构造数字空间的mask

我们将decoder端的词汇空间划分成三类，$V_{op}$指的是运算符加减乘除的空间，$V_{con}$指的就是常数空间。我所指的数字空间对应的就是论文中的$n_P$。

print("在当前的batch中，每一个问题中出现了几个数字 : ",num_size_batch)
num_mask = []
max_num_size = max(num_size_batch) + len(generate_nums)
#我们会按照当前batch中出现数字次数最多的那个问题对应的数字出现的次数作为decoder端的输出数字空间(这对应的就是论文中的nP，见公式5)
for i in num_size_batch:
    d = i + len(generate_nums)
    num_mask.append([0] * d + [1] * (max_num_size - d))
num_mask = torch.ByteTensor(num_mask)
print("当前的batch中，每一个样本对应的数字的mask : ",num_mask)
#0代表没有pad，1代表pad

如下图所示

注意这个num_mask是不包括加减乘除的

构造输入张量

unk = output_lang.word2index["UNK"]
input_var = torch.LongTensor(input_batch).transpose(0, 1)
target = torch.LongTensor(target_batch).transpose(0, 1)
padding_hidden = torch.FloatTensor([0.0 for _ in range(predict.hidden_size)]).unsqueeze(0)
batch_size = len(input_length)

也就是说输入了两个句子，第一个句子比较长，对应的表达式也比较长，第二个句子比较短，所以要pad

获得encoder 的输出，并且提取出每一个问题的根目标向量

encoder_outputs, problem_output = encoder(input_var, input_length)
print(encoder_outputs.size())
print(problem_output.size())
#problem_output就是每一个问题的根目标向量
class TreeNode:  # the class save the tree node
    def __init__(self, embedding, left_flag=False):
        self.embedding = embedding
        self.left_flag = left_flag
        
node_stacks = [[TreeNode(_)] for _ in problem_output.split(1, dim=0)]
#node_stacks就是将batch个样本的根目标向量拿出来，存储到节点中
print(problem_output)
for i in range(batch_size):
    print(node_stacks[i][0].embedding)

encoder返回两个tensor，第一个tensor是encoder_outputs，代表的是整个问题句子中语义向量。第二个tensor是problem_output，它是前向GRU的最后一个单词的向量加上反向GRU的最后一个单词的向量，所以它就是论文中所提到的每一个问题的根目标向量$\mathbf{q}$。node_stacks这个列表初始时刻存储的就是每一个问题的根目标向量

获得num_embedding

#node_stacks就是每一个问题的根节点
max_target_length=max(target_length)
print("当前 batch中，所有句子对应的equation中最长的表达式的长度　: ",max_target_length)
print("我们在当前batch的解码过程中，以最长的表达式作为当前batch解码端的终止长度")

print("当前batch中，每一个问题出现的数字在该问题中的位置 : ",num_pos)
copy_num_len = [len(_) for _ in num_pos]
print("当前batch中，每一个问题出现的数字的个数　: ",copy_num_len)
num_size=max(copy_num_len)
all_nums_encoder_outputs = get_all_number_encoder_outputs(encoder_outputs, num_pos, batch_size, num_size,
                                                          encoder.hidden_size)
print(all_nums_encoder_outputs.size())

这里面的get_all_number_encoder_outputs看名字就知道是为了获得问题中数字对应的embedding。我们可以打印出来证实一下：

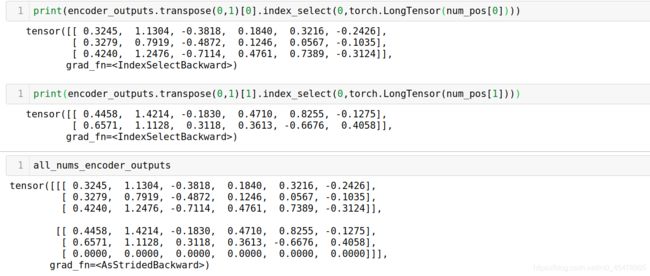
是不是不出所料啊，all_nums_encoder_outputs存储的就是当前batch中，每一个问题出现的数字对应的embedding,也就是论文中的${\mathbf{h}}_{loc(y,P)}^p$

需要注意的是因为第二个问题只出现了两个数字，所以要补一行0向量。

还记得前面我们说过吗，每一个节点都有三个成分：根目标向量；预测的token；以及子树嵌入.下面我们初始化每一个根节点，

all_node_outputs = []
num_start = output_lang.num_start
print(output_lang.word2index)
print(num_start)
embeddings_stacks = [[] for _ in range(batch_size)]
left_childs = [None for _ in range(batch_size)]

现在根节点已经初始化好了，也就是说每一个根节点的目标向量就是对应的problem_output，每一个根节点的左子树初始化为None

开始构建树

我们再打印一次当前的batch

print_data(input_batch)
print_data(batch_datas)
print_data(target_batch)
print_data(batch_orig_pairs)
print(output_lang.word2index)

看好了啊，现在我们输入的句子是什么已经清楚了，下面我们一步一步一步一步一步一步的来看接下来的过程：

for i in range(max_target_length)，这里面的max_target_length就是当前batch个问题中最长的expression。我们肯定要以最长的为准，因为短的表达式我们可以提前结束，长的表达式必须到达指定长度才可以。

我们来看predict，它的目的就是预测token，根据公式７，我们现在只是知道q,还不知道c和e(y|P)。

class Prediction(nn.Module):
    # a seq2tree decoder with Problem aware dynamic encoding

    def __init__(self, hidden_size, op_nums, input_size, dropout=0.5):
        super(Prediction, self).__init__()

        # Keep for reference
        self.hidden_size = hidden_size
        self.input_size = input_size
        self.op_nums = op_nums#op_nums=output_lang.n_words - copy_nums - 1 - len(generate_nums)
        #op_nums就是４，也就是加减乘除

        # Define layers
        self.dropout = nn.Dropout(dropout)

        self.embedding_weight = nn.Parameter(torch.randn(1, input_size, hidden_size))
        #input_size=len(generate_nums)，也就是2，代表3.14和1两个常数

        # for Computational symbols and Generated numbers
        self.concat_l = nn.Linear(hidden_size, hidden_size)
        self.concat_r = nn.Linear(hidden_size * 2, hidden_size)
        self.concat_lg = nn.Linear(hidden_size, hidden_size)
        self.concat_rg = nn.Linear(hidden_size * 2, hidden_size)

        self.ops = nn.Linear(hidden_size * 2, op_nums)

        self.attn = TreeAttn(hidden_size, hidden_size)
        self.score = Score(hidden_size * 2, hidden_size)

    def forward(self, node_stacks, left_childs, encoder_outputs, num_pades, padding_hidden, seq_mask, mask_nums):
    	'''
    	node_stacks就是每一个节点，它是TreeNode的对象，包含的是该节点的目标向量q
    	encoder_outputs是用来计算attention的，看公式6
    	num_pades就是all_num_encoder_outputs，它是问题中每一个数字的embedding，对应的是论文中的h_{loc(y,P)}^p，它是e(y|P)的一部
    	padding_hidden, seq_mask, mask_nums这几个不解释了，构造mask的，对于理解模型无关
    	'''
        current_embeddings = []

        for st in node_stacks:
            if len(st) == 0:
                current_embeddings.append(padding_hidden)
            else:
                current_node = st[-1]#current_node.embedding就是当前节点的目标向量q
                current_embeddings.append(current_node.embedding)

        current_node_temp = []
        for l, c in zip(left_childs, current_embeddings):
            if l is None:
                c = self.dropout(c)
                g = torch.tanh(self.concat_l(c))
                t = torch.sigmoid(self.concat_lg(c))
                current_node_temp.append(g * t)#这几行公式论文中找不到
                #ｃ是每一个节点的目标向量
            else:
                ld = self.dropout(l)
                c = self.dropout(c)
                g = torch.tanh(self.concat_r(torch.cat((ld, c), 1)))
                t = torch.sigmoid(self.concat_rg(torch.cat((ld, c), 1)))
                current_node_temp.append(g * t)

        current_node = torch.stack(current_node_temp)#

        current_embeddings = self.dropout(current_node)

        current_attn = self.attn(current_embeddings.transpose(0, 1), encoder_outputs, seq_mask)
        current_context = current_attn.bmm(encoder_outputs.transpose(0, 1))  # B x 1 x N

        # the information to get the current quantity
        batch_size = current_embeddings.size(0)
        # predict the output (this node corresponding to output(number or operator)) with PADE

        repeat_dims = [1] * self.embedding_weight.dim()
        repeat_dims[0] = batch_size
        embedding_weight = self.embedding_weight.repeat(*repeat_dims)  # B x input_size x N
        #self.embedding_weight代表的是常数的embedding,size()==(2,embed_dim)
        #常数的表示向量对于所有问题都是通用的，所以我们可以把它重复batch_size次
        embedding_weight = torch.cat((embedding_weight, num_pades), dim=1)  # B x O x N
        #num_pades就是当前的batch个问题中，每一个问题中数字的embedding
		#此时的embedding_weight.size()==(batch_size,2+3,dim)，所以说此时的embedding_weigth相当于一个查找表，用来查找常数和问题中数字的嵌入向量
        leaf_input = torch.cat((current_node, current_context), 2)
        #相当于结合了q和c，leaf_input.size()==(batch_size,hidden_dim*2)
        leaf_input = leaf_input.squeeze(1)
        leaf_input = self.dropout(leaf_input)

        # p_leaf = nn.functional.softmax(self.is_leaf(leaf_input), 1)
        # max pooling the embedding_weight
        embedding_weight_ = self.dropout(embedding_weight)
        num_score = self.score(leaf_input.unsqueeze(1), embedding_weight_, mask_nums)
        #关于Score的解释见下面，看完了score的解释再回头看这个
        #现在我们知道num-score.size()==(batch_size,2+3)

        # num_score = nn.functional.softmax(num_score, 1)

        op = self.ops(leaf_input)#ops就是用来预测当前的token是不是运算符的
        #op.size()==(batch_size,4)
        #而num_score是用来预测当前的token是不是数字的，是数字的话是论文中的数字还是常数
		#current_context就是论文中c,current_node姑且认为是论文中的q，但是计算的方式在论文中没有提及
        return num_score, op, current_node, current_context, embedding_weight

下面解释下score

class Score(nn.Module):
    def __init__(self, input_size, hidden_size):
        super(Score, self).__init__()
        self.input_size = input_size#input_size=hidden_size*2
        self.hidden_size = hidden_size
        self.attn = nn.Linear(hidden_size + input_size, hidden_size)
        self.score = nn.Linear(hidden_size, 1, bias=False)

    def forward(self, hidden, num_embeddings, num_mask=None):
    	'''
    	hidden是目标向量q和上下文向量c的结合,hidden.size()==(batch_size,dim*2)
    	num_embeddings是数字的嵌入表示，包括问题中的数字和常数，size()==(batch_size,2+3,dim)
    	其中2是指在所有的问题中有两个常数，3是指当前的batch中出现数字次数最多的那个问题出现了三次数字
    	'''
        max_len = num_embeddings.size(1)
        repeat_dims = [1] * hidden.dim()
        repeat_dims[1] = max_len
        hidden = hidden.repeat(*repeat_dims)  # B x O x H
        # For each position of encoder outputs
        this_batch_size = num_embeddings.size(0)
        energy_in = torch.cat((hidden, num_embeddings), 2).view(-1, self.input_size + self.hidden_size)
        #注意注意这个energy_in，它将c,q,num_embeddings连接起来，这正对应着公式7中的[q,c,e(y|P)]
        #只不过此时的e(y|P)不包含运算符的嵌入表示向量，所以预测出来的分数是数字的分数，不预测运算符
        #这也是为什么代码中起名字叫num_score，指的就是预测的所有数字的分数。
        score = self.score(torch.tanh(self.attn(energy_in)))  # (B x O) x 1
        score = score.squeeze(1)
        score = score.view(this_batch_size, -1)  # B x O
        if num_mask is not None:
            score = score.masked_fill_(num_mask, -1e12)
            #这行代码很重要很重要，因为我们知道我们已经将所有数字给pad了，也就是由于第一个问题有3个数字
            #第二个问题有两个数字，所以第二个问题的数字向量的最后一位其实应该是0，所以我们必须把这个位置赋值为很小的数字，这样做
            #softmax才能忽略这个位置，不然模型就会预测出不存在的数字
        return score

现在我们结束了predict:

for t in range(max_target_length):
    num_score, op, current_embeddings, current_context, current_nums_embeddings = predict(
        node_stacks, left_childs, encoder_outputs, all_nums_encoder_outputs, padding_hidden, seq_mask, num_mask)

• num_score.size()==(batch_size,2+3)，这个tensor的含义是预测当前节点的token是数字的分数，这里的数字包括常数和问题中的数字
• op.size()==(batch_size,4)，这个tensor的含义是预测当前节点的token是运算符的分数。
• current_embeddings.size()==(batch_size,dim)，这个tensor指的是当前节点的目标向量
• current_context.size()==(batch_size,dim)，这个tensor指的是当前节点的上下文信息向量，它是利用目标向量和encoder_outputs做注意力计算得到的。
• current_nums_embeddings.size()==(batch_size,2+3,dim)。这个tensor指的是当前节点对应的数字的embedding，前两个是常数的嵌入向量

print("当前的token可能是哪一个运算符 : ",op)
print("当前的token可能是常数还是问题中的数字的 : ",num_score)
print("当前节点的目标向量q : ",current_embeddings)
print("当前节点的上下文向量c : ",current_context)
print("当前节点对应的e(y|P)中是数字(包含常数或者问题中的数字)的embedding : ",current_nums_embeddings)

我们可以观察到，num_score的第二个问题对应的向量的最后一个值是-1e12，因为这个位置是pad的；此外current_nums_embeddings的两个问题对应的数字嵌入向量的前两个值都是一样的。因为常数嵌入对于所有问题都是适用的。

outputs = torch.cat((op, num_score), 1)#显然中的显然，outputs代表的就是公式(7)中的s(y|q,c,P)
print("预测当前节点对应的token : ",outputs)
all_node_outputs.append(outputs)
print("当前的batch个样本中是否出现了重复数字 : ",num_stack_batch)
print("在output_lang.word2index中数字的起始下标 : ",num_start)
print(output_lang.word2index)
print(unk)

outputs将op和num_score连接起来，那么显然outputs就是论文中的$s(y|\mathbf{q},\mathbf{c},P)$，他代表的就是预测当前节点是哪一个token，其中前四个位置是预测为运算符的分数，后面的位置是预测为数字的分数

我们接下来进入generate_tree_input，在这之前我们看看target是什么

target就是每一个问题的前缀数学表达式，我们现在t=0,所以target[0]就是两个问题对应的表达式的第一个token。显然第一个问题的表达式的第一个字符是-；第二个问题的表达式的第一个字符是*；

现在把模型预测的outputs和target送入generate_tree_input

def generate_tree_input(target, decoder_output, nums_stack_batch, num_start, unk):
    # when the decoder input is copied num but the num has two pos, chose the max
    # decoder_output就是上面的ouputs，它的size==(batch_size,4+2+3)，也就是预测当前的token是
    #运算符还是数字的分数
    target_input = copy.deepcopy(target)
    #target的长度就是batch_size
    for i in range(len(target)):
        if target[i] == unk:
        	#这里面unk=11，target[i]=unk的唯一可能就是当前的问题出现了重复的数字
        	#而出现重复的数字时，论文的做法是保留数字在表达式中，这就是的表达式出现了除常数1和3.14
        	#以外的数字，而这个数字不在output_lang.word2index中，所以就被替换为了unk
            num_stack = nums_stack_batch[i].pop()
            #nums_stack记录的正是重复数字在nums中的位置，nums中记录的是问题中出现的所有数字的位置
            max_score = -float("1e12")
            for num in num_stack:
            	#num的含义就是该数字在nums中的位置
            	#显然decoder[i,4+num]就表示预测该数字的分数
            	#由于有两个重复的数字，他们出现在不同的位置，所以我们取较大的分数的那个位置的数字作为预测值
                if decoder_output[i, num_start + num] > max_score:
                    target[i] = num + num_start
                    max_score = decoder_output[i, num_start + num]
        if target_input[i] >= num_start:
            target_input[i] = 0
    return torch.LongTensor(target), torch.LongTensor(target_input)
    #注意这里面对于target中出现unk位置的情况，我们已经将unk替换为对应的数字的预测分数，所以此时的target才是真正的target
    #但是target_input将那些凡是数字的target全部替换掉是为什么呢

现在我们的代码目前是:

target_t, generate_input = generate_tree_input(target[t].tolist(), outputs, nums_stack_batch, num_start, unk)
target[t] = target_t

根据上面的解释我们知道，假如所有问题中不出现重复的数字，那么target[t]=target_t这一步是不用做的。

接下来我们来看generate

class GenerateNode(nn.Module):
    def __init__(self, hidden_size, op_nums, embedding_size, dropout=0.5):
        super(GenerateNode, self).__init__()
		
        self.embedding_size = embedding_size
        self.hidden_size = hidden_size

        self.embeddings = nn.Embedding(op_nums, embedding_size)#op_nums是4
        self.em_dropout = nn.Dropout(dropout)
        self.generate_l = nn.Linear(hidden_size * 2 + embedding_size, hidden_size)
        self.generate_r = nn.Linear(hidden_size * 2 + embedding_size, hidden_size)
        self.generate_lg = nn.Linear(hidden_size * 2 + embedding_size, hidden_size)
        self.generate_rg = nn.Linear(hidden_size * 2 + embedding_size, hidden_size)

    def forward(self, node_embedding, node_label, current_context):
    	'''
    	node_embedding.size()==(batch_size,1,dim)==current_context.size()
    	node_label的长度是batch_size，取值在[0,4)之间，因为在generate_input中我们已经把不是运算符的标签
    	全部替换为0
    	'''
        node_label_ = self.embeddings(node_label)#(batch_size,dim)
        #也就是将每一个运算符嵌入成一个向量
        node_label = self.em_dropout(node_label_)
        node_embedding = node_embedding.squeeze(1)
        current_context = current_context.squeeze(1)
        node_embedding = self.em_dropout(node_embedding)
        current_context = self.em_dropout(current_context)
		#这三个tensor的size都是(batch_size,dim)
        l_child = torch.tanh(self.generate_l(torch.cat((node_embedding, current_context, node_label), 1)))
        l_child_g = torch.sigmoid(self.generate_lg(torch.cat((node_embedding, current_context, node_label), 1)))
        r_child = torch.tanh(self.generate_r(torch.cat((node_embedding, current_context, node_label), 1)))
        r_child_g = torch.sigmoid(self.generate_rg(torch.cat((node_embedding, current_context, node_label), 1)))
        l_child = l_child * l_child_g
        r_child = r_child * r_child_g
        return l_child, r_child, node_label_
        #l_child是左子树,r_child是右子树,node_label_是对应的运算符的向量表示

下面我们进入到代码：

left_child, right_child, node_label = generate(current_embeddings, generate_input, current_context)
left_childs = []
for idx, l, r, node_stack, i, o in zip(range(batch_size), left_child.split(1), right_child.split(1),
                                               node_stacks, target[t].tolist(), embeddings_stacks):

• 从这里我们就知道了，原来current_embeddings对应的不是目标向量,node_stacks里面才是节点的目标向量
• current_embeddings只不过是将目标向量通过了一层全链接层，这也是为什么后来的generate中左右子树都只有一层全连接层，因为目标向量已经通过了一次全连接层
• 但是在预测outputs的时候又是用的current_embeddings，这与论文中的公式7不符合
• left_child是左子树,right_child是右子树的嵌入，这也是为什么要将target中的数字替换为0，因为我们一开始默认所有节点都是运算符，都是有子树的

left_childs = []
print("当前的标签 : ",target[t].tolist() )
print("当前的batch个问题对应的节点 : ",node_stacks)
for idx, l, r, node_stack, i, o in zip(range(batch_size), left_child.split(1), right_child.split(1),
                                       node_stacks, target[t].tolist(), embeddings_stacks):
    if len(node_stack) != 0:
        node = node_stack.pop()
    else:
        left_childs.append(None)
        continue
    #node就是目标向量
    if i < num_start:
        #如果当前的标签是运算符(注意target是真的标签，没有被替换的，只是其中的unk被替换为真正的数字)
        node_stack.append(TreeNode(r))
        node_stack.append(TreeNode(l, left_flag=True))
        o.append(TreeEmbedding(node_label[idx].unsqueeze(0), False))#node就是运算符的向量表示
        #False表示当前还有子目标
    else:
        #当前的标签是数字，current_nums_embeddings中记录的是所有数字的embeddings，所以要i-num_start才能对应上正确的位置
        #current_embedding.size()==(batch_size,2+3,dim)
        current_num = current_nums_embeddings[idx, i - num_start].unsqueeze(0)
        #current_num就是这个数字的embedding
        while len(o) > 0 and o[-1].terminal:
            sub_stree = o.pop()
            op = o.pop()
            current_num = merge(op.embedding, sub_stree.embedding, current_num)
            #如果len(o)>0，merge就是将两个子目标的嵌入向量合并作为该节点的subtree_embedding，对应的是论文中公式12
        o.append(TreeEmbedding(current_num, True))#current_num和node_label是对应的
        #True表示到达叶子节点
    if len(o) > 0 and o[-1].terminal:
        left_childs.append(o[-1].embedding)
    else:
        left_childs.append(None)

执行完之后：

也就是说，执行完上述流程之后，我们将这两个问题的根节点的左右子树找到了。

我们再次执行一遍上述流程,t+=1

得到了最左侧的节点：

正是数字对应的embeddings

执行完真个max_target_length后，我们有：

显然all_nodes_outputs.size()==(batch_size,max_target_length,4+2+3)
代表的含义就是预测的token的分数，一共有max_target_length个时间步，注意的是不同的batch，时间步也不同，取决于那个batch中最长的表达式的长度。
而且不同的batch，最后的维度，也就是4+2+3中的3也是不一样的
取决于那个batch中所有问题中出现数字次数最多的那个问题中数字出现的次数

最后终于到了

loss = masked_cross_entropy(all_node_outputs, target, target_length)
loss.backward()

train_tree也就结束了，整个训练过程就是这样

接下来来看预测阶段

print(len(test_pairs))
for i,pair in enumerate(test_pairs):
    if pair[-1]!=[]:
        demo_pair=pair
        break
print("我们用下面这个example作为测试阶段的演示",demo_pair)
print("对应的问题是　: ",data[i])

可以看到，这个例子中，5月份的5也是数字，所以此时的nums=[5,16.5,2.1,5]，nums中出现了重复数字。而且对应的num_stack记录的就是重复数字在nums中的位置，所以num_stack=[[0,3]]。

下面我们来看evaluate_tree

首先来看输入:

demo=demo_pair
input_seq=demo[0]
input_seq_length=demo[1]
output_seq=demo[2]
output_seq_length=demo[3]
nums=demo[4]
num_pos=demo[5]
num_stack=demo[6]
seq_mask = torch.ByteTensor(1, input_seq_length).fill_(0)
input_var = torch.LongTensor(input_seq).unsqueeze(1)
num_mask = torch.ByteTensor(1, len(num_pos) + len(generate_nums)).fill_(0)
#由于是一个一个样本的计算，所以不需要seq_mask和num_mask
padding_hidden = torch.FloatTensor([0.0 for _ in range(predict.hidden_size)]).unsqueeze(0)
batch_size = 1
print(num_mask)
print(seq_mask)
print(num_pos)

通过encoder后，得到encoder_outputs和这个问题的根节点向量

encoder_outputs, problem_output = encoder(input_var, [input_seq_length])
print("当前问题的根节点向量q : ",problem_output)
print(encoder_outputs.size())#(seq_length,1,dim)

得到node_stacks

node_stacks = [[TreeNode(_)] for _ in problem_output.split(1, dim=0)]
num_size=len(num_pos)
print("当前这个问题中有%d个数字出现"%num_size)
print(node_stacks[0][0].embedding)

得到问题中数字对应的嵌入all_nums_encoder_outputs

all_nums_encoder_outputs = get_all_number_encoder_outputs(encoder_outputs, [num_pos], batch_size, num_size,
                                                          encoder.hidden_size)
print("当前这个问题中所有数字对应的embedding : ",all_nums_encoder_outputs)#(4,dim)因为有四个数字

num_start = output_lang.num_start
# B x P x N
embeddings_stacks = [[] for _ in range(batch_size)]
left_childs = [None for _ in range(batch_size)]

def copy_list(l):
    r = []
    if len(l) == 0:
        return r
    for i in l:
        if type(i) is list:
            r.append(copy_list(i))
        else:
            r.append(i)
    return r

class TreeBeam:  # the class save the beam node
    def __init__(self, score, node_stack, embedding_stack, left_childs, out):
        self.score = score
        self.embedding_stack = copy_list(embedding_stack)
        self.node_stack = copy_list(node_stack)
        self.left_childs = copy_list(left_childs)
        self.out = copy.deepcopy(out)

MAX_OUTPUT_LENGTH = 45
max_length=MAX_OUTPUT_LENGTH
print(node_stacks,embeddings_stacks,left_childs)

beams = [TreeBeam(0.0, node_stacks, embeddings_stacks, left_childs, [])]

从这里开始进入for循环

t=0
current_beams=[]
b=beams.pop()
left_childs = b.left_childs
print("predict的输入如下 : ")
print(b.node_stack)
print(left_childs)
print(padding_hidden)

num_score, op, current_embeddings, current_context, current_nums_embeddings = predict(
    b.node_stack, left_childs, encoder_outputs, all_nums_encoder_outputs, padding_hidden,
    seq_mask, num_mask)
print("num_score指的是预测token是数字的分数 (长度应该是2+4)",num_score)
print("op指的是预测token是运算符的分数 (长度应该是4)",op)
print("current_embeddings指的是根目标向量经过一层全连接层后 : ",current_embeddings)
print("上下文向量c : ",current_context)
print("当前这个对应的数字嵌入，也就是在原来的基础上加上常数的嵌入(需要特别注意的是predi \
      ct类只有一个，而关于常数的嵌入矩阵是predict的一个成员变量，所以对于所有的问题，都是通用的)",current_nums_embeddings)

往回找一下，就会发现当前current_num_embeddings的前两行和前面的current_num_embeddings的前两行是一样的

获得预测该token的概率

outputs=torch.cat((op,num_score),dim=1)#对应的就是论文中的s(y|q,c,P)
print(outputs)
print(outputs.size())#(1,10) 这里的10=4+2+4，第一个4是加减乘除,2代表的是1和3.14，第二个4是因为这个问题中出现了四个数字
out_score = nn.functional.log_softmax(torch.cat((op, num_score), dim=1), dim=1)
print(out_score)

print(beam_size)
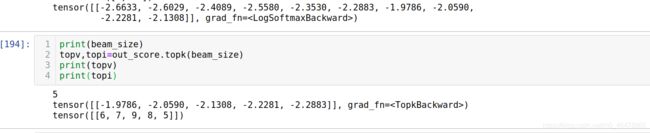
topv,topi=out_score.topk(beam_size)
print(topv)
print(topi)

当我们取argmax(output_score)时，得到的下标就是我们要预测的那个token在output_lang.word2index中对应的下标

topv_zip=topv.split(1,dim=1)
topi_zip=topi.split(1,dim=1)
vi=0
tv=topv_zip[vi]
ti=topi_zip[vi]
print(tv,ti)

一共要做5路树搜索

current_node_stack = copy_list(b.node_stack)
current_left_childs = []
current_embeddings_stacks = copy_list(b.embedding_stack)
current_out = copy.deepcopy(b.out)

out_token = int(ti)
print("预测的token对应的id ",out_token)
print("预测的token是 : ",output_lang.index2word[out_token])
current_out.append(out_token)

#由于此时的output_token>num_start
current_num = current_nums_embeddings[0, out_token - num_start].unsqueeze(0)
#output_token是6，6-num_start=2，而current_num_embeddings的第三个元素正好是N0对应embedding
print(current_embeddings_stacks)#current_embeddings_stacks[0]==0
current_embeddings_stacks[0].append(TreeEmbedding(current_num, True))
if len(current_embeddings_stacks[0]) > 0 and current_embeddings_stacks[0][-1].terminal:
    current_left_childs.append(current_embeddings_stacks[0][-1].embedding)
current_beams.append(TreeBeam(b.score+float(tv), current_node_stack, current_embeddings_stacks,
                              current_left_childs, current_out))

按照上述流程走完一遍，我们知道：

1. current_embeddings_stacks存储的是子树嵌入
2. current_node_stacks存储的是目标向量
3. b.score记录的是每个时间步预测一个token对应的分数

计算前缀结果：

def out_expression_list(test,output_lang,num_list,num_stack):
    max_index=output_lang.n_words
    result=[]
    for i in test:
        if i<max_index-1:
            #也就是说i不是unk对应的
            token=output_lang.index2word[i]
            if token[0]=='N':
                #说明这个是问题中出现的数字，所以token[1:]这个数字对应的就是该数字在num_list中的位置，最后就可以根据num_list还原回这个数字
                if int(token[1:])>=len(num_list):
                    #说明此时预测的token虽然是数字，但是已经超出了该问题中出现数字的次数，
                    #这种情况主要是因为pad引起的，因为每一个问题中出现数字的次数显然不同
                    #所以在预测那些出现数字次数比较少的问题的表达式的时候，由于decoder端的词汇包含了当前batch中出现数字次数最多的
                    #那个次数，就会出现预测的数字对应的位置比实际问题中出现的数字次数还要大
                    return None
                
                result.append(num_list[int(token[1:])])
            else:
                result.append(token)#此时的token可能是加减乘除或者1和3.14，不需要替换
        else:
            #也就是说此时的i是对应着unk，那么说明出现了重复数字,num_stack必然不空
            assert len(num_stack)>1
            duplicated_number_position=num_stack.pop()
            #duplicated_number_position必然有两个数字，代表的是重复数字在num_list中的位置
            c=num_list[duplicated_number_position[0]]#0或者1无所谓，因为都是一样的
            result.append(c)#我们同样将预测的unk替换为了原来的真实的数字
    return result

#关于计算前缀表达式的代码参考原论文

def compute_prefix_tree_result(test_res,test_tar,output_lang,num_list,num_stack):
    '''
    num_list就是nums，也就是问题中所有出现的数字
    num_stack就是记录的问题中重复数字在num_list中的位置
    '''
    if len(num_stack)==0 and test_res==test_tar:
        #没有出现重复数字，而且预测的表达式的与真实的表达式完全一致
        return True,True
    test = out_expression_list(test_res, output_lang, num_list,copy.deepcopy(num_stack))
    print("预测的前缀表达式 : ",test)
    tar = out_expression_list(test_tar, output_lang, num_list, copy.deepcopy(num_stack))
    print("实际的前缀表达式 : ",tar)
    if test is None:
        return False,False
    if test==tar:
        return True,True
    
    try:
        if abs(compute_prefix_expression(test)-compute_prefix_expression(tar))<1e-4:
            return True,False
        else:
            return False,False
    except:
        return False,False
    

我们举个例子

demo_target=[1, 3, 0, 6, 1, 4, 7, 1, 4, 8, 6]
demo_predict=[0,1,6,4,7]
compute_prefix_tree_result(demo_predict,demo_target,output_lang,num_list=nums,num_stack=[])

其中out_expression_list的作用就是将预测的id替换成对应的token，

• 如果预测的id是0,1,2,3中的一个，那么直接替换为对应的加减乘除。
• 如果id是4或者5，那么替换为对应的1或者3.14。
• 如果id是6,7,…直到unk所在的前一个id，那么根据output_lang.index2word我们就可以得到对应的Ni，这个i取决于模型的预测，
  • 如果模型预测的这个i值大于该问题中出现的数字的次数，那么直接返回None，因为此时模型预测的数字根本就不在问题中出现过
  • 如果模型预测的这个i值小于该问题中出现的数字的次数，那么就可以还原这个预测的数字了，因为这个i值正好对应的是num_list中的下标索引，num_list[i]就是问题中的数字
• 另一方面，如果模型预测的id是unk，那么说明问题中出现了重复数字，此时需要num_stack来还愿，因为num_stack记录的是重复数字在num_list中的位置，所以根据num_stack和num_list就可以找到原数字

终于结束了