机器学习实战笔记5—支持向量机

注：此系列文章里的部分算法和深度学习笔记系列里的内容有重合的地方，深度学习笔记里是看教学视频做的笔记，此处文章是看《机器学习实战》这本书所做的笔记，虽然算法相同，但示例代码有所不同，多敲一遍没有坏处，哈哈。（里面用到的数据集、代码可以到网上搜索，很容易找到。）。Python版本3.6

机器学习十大算法系列文章：

机器学习实战笔记1—k-近邻算法

机器学习实战笔记2—决策树

机器学习实战笔记3—朴素贝叶斯

机器学习实战笔记4—Logistic回归

机器学习实战笔记5—支持向量机

机器学习实战笔记6—AdaBoost

机器学习实战笔记7—K-Means

机器学习实战笔记8—随机森林

机器学习实战笔记9—人工神经网络

此系列源码在我的GitHub里：https://github.com/yeyujujishou19/Machine-Learning-In-Action-Codes

一，算法原理：

参考上一篇文章：深度学习基础课程1笔记-支持向量机（SVM）

二，算法的优缺点：

优点：

1）对于线性不可分的情况可以通过核函数，映射到高维特征空间实现线性可分。

2）SVM学习问题可以表示为凸优化问题，因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法（如基于规则的分类器和人工神经网络）都采用一种基于贪心学习的策略来搜索假设空间，这种方法一般只能获得局部最优解。

3）小集群分类效果好。

缺点：

1）SVM仅仅只限于一个二类分类问题，对于多分类问题解决效果并不好。

2）仅局限于小集群样本，对于观测样本太多时，效率较低。

3）寻求合适的核函数相对困难。

三，实例代码：

SMO算法：是一种用于训练SVM的强大算法，它将大的优化问题分解为多个小的优化问题来进行求解。而这些小优化问题往往很容易求解，并且对它们进行顺序求解和对整体求解结果是一致的。在结果一致的情况下，显然SMO算法的求解时间要短很多，这样当数据集容量很大时，SMO就是一致十分高效的算法。

SMO算法的目标是找到一系列alpha和b，而求出这些alpha，我们就能求出权重w，这样就能得到分隔超平面，从而完成分类任务

SMO算法的工作原理是：每次循环中选择两个alpha进行优化处理。一旦找到一对合适的alpha，那么就增大其中一个而减少另外一个。这里的"合适",意味着在选择alpha对时必须满足一定的条件，条件之一是这两个alpha不满足最优化问题的kkt条件，另外一个条件是这两个alpha还没有进行区间化处理。

SMO算法推导

下面是简易版SMO算法需要用到的一些功能，我们将其包装成函数，需要时调用即可：

from numpy import *
from time import sleep
import matplotlib.pyplot as plt
import numpy as np

#SMO算法相关辅助中的辅助函数
# 1 解析文本数据函数，
# 提取每个样本的特征组成向量，添加到数据矩阵
# 添加样本标签到标签向量
def loadDataSet(fileName):               #文件路径
    dataMat = []; labelMat = []  #数据列表和标签列表
    fr = open(fileName)          #打开文件
    for line in fr.readlines():  #逐行读取
        lineArr = line.strip().split('\t')  #去除首尾空格，并拆分字符串
        dataMat.append([float(lineArr[0]), float(lineArr[1])]) #将第一二列加入数据列表
        labelMat.append(float(lineArr[2])) #将第三列加入标签列表
    return dataMat,labelMat

# 函数说明:数据可视化
# dataMat - 数据矩阵
# labelMat - 数据标签
# Returns:无
def showDataSet(dataMat, labelMat):
    data_plus = []                                  #正样本
    data_minus = []                                 #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              #转换为numpy矩阵
    data_minus_np = np.array(data_minus)            #转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1])   #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图
    plt.show()


#2 在样本集中采用随机选择的方法选取第二个不等于第一个alphai的
#优化向量alphaj
def selectJrand(i,m):
    j=i
    while (j==i):
        j = int(random.uniform(0,m))
    return j

#3 约束范围L<=alphaj<=H内的更新后的alphaj值
def clipAlpha(aj,H,L):
    if aj > H: 
        aj = H
    if L > aj:
        aj = L
    return aj

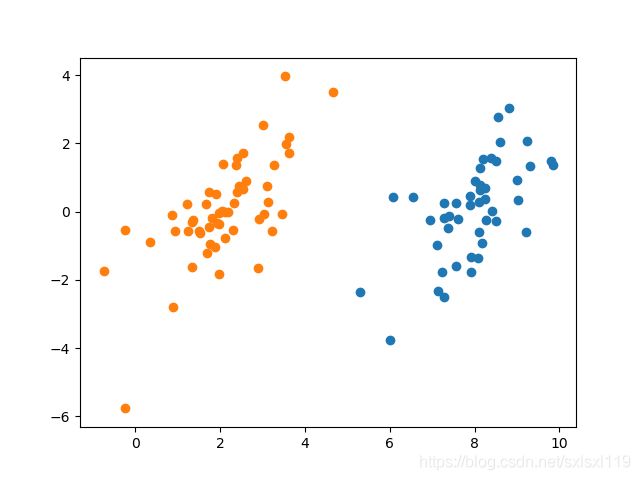
dataMat, labelMat=loadDataSet('testSet.txt')
showDataSet(dataMat, labelMat)

代码结果：

 

SMO算法的伪代码：

#SMO算法的伪代码
#创建一个alpha向量并将其初始化为0向量
#当迭代次数小于最大迭代次数时(w外循环)
    #对数据集中每个数据向量(内循环):
    #如果该数据向量可以被优化：
        #随机选择另外一个数据向量
        #同时优化这两个向量
        #如果两个向量都不能被优化，退出内循环
#如果所有向量都没有被优化，增加迭代次数，继续下一次循环

 SMO算法的代码：

#dataMat    ：数据列表
#classLabels：标签列表
#C          ：权衡因子（增加松弛因子而在目标优化函数中引入了惩罚项）
#toler      ：容错率
#maxIter    ：最大迭代次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose() # 将列表形式转为矩阵或向量形式
    b = 0; m,n = shape(dataMatrix)   # 初始化b=0，获取矩阵行列
    alphas = mat(zeros((m,1)))       # 初始化alpha参数，设为0
    iter = 0                         #迭代次数为0
    while (iter < maxIter):          #当迭代次数小于最大迭代次数时(w外循环)
        alphaPairsChanged = 0        #改变的alpha对数
        for i in range(m):           #遍历样本集中样本
            # 步骤1：计算误差Ei
            fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b #计算支持向量机算法的预测值
            Ei = fXi - float(labelMat[i])#计算预测值与实际值的误差
            #优化alpha，更设定一定的容错率。
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i,m) #随机选择另一个与alpha_i成对优化的alpha_j
                # 步骤1：计算误差Ej
                fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b #计算第二个变量对应数据的预测值
                Ej = fXj - float(labelMat[j]) #计算与测试与实际值的差值
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy(); #记录alphai和alphaj的原始值，便于后续的比较
                # 步骤2：计算上下界L和H
                if (labelMat[i] != labelMat[j]):  #如果两个alpha对应样本的标签不相同
                    L = max(0, alphas[j] - alphas[i])  #求出相应的上下边界
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print ("L==H"); continue
                # 根据公式计算未经剪辑的alphaj
                # ------------------------------------------
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                # 如果eta>=0,跳出本次循环
                if eta >= 0: print ("eta>=0"); continue
                # 步骤4：更新alpha_j
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                # 步骤5：修剪alpha_j
                alphas[j] = clipAlpha(alphas[j],H,L)
                # ------------------------------------------
                # 如果改变后的alphaj值变化不大，跳出本次循环
                if (abs(alphas[j] - alphaJold) < 0.00001): print ("alpha_j变化太小"); continue
                # 步骤6：更新alpha_i
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                # 步骤7：更新b_1和b_2
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                # 步骤8：根据b_1和b_2更新b
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                # 否则如果0 alphas[j]): b = b2
                # 否则，alphai，alphaj=0或C
                else: b = (b1 + b2)/2.0
                # 统计优化次数
                alphaPairsChanged += 1
                print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
        # 最后判断是否有改变的alpha对，没有就进行下一次迭代
        if (alphaPairsChanged == 0): iter += 1
        # 否则，迭代次数置0，继续循环
        else: iter = 0
        print("迭代次数: %d" % iter)
    # 返回最后的b值和alpha向量
    return b,alphas

# 函数说明:分类结果可视化
# dataMat - 数据矩阵
# w - 直线法向量
# b - 直线解决
# Returns:无
def showClassifer(dataMat, w, b):
    #绘制样本点
    data_plus = []                                  #正样本
    data_minus = []                                 #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              #转换为numpy矩阵
    data_minus_np = np.array(data_minus)            #转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) #负样本散点图
    #绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #找出支持向量点
    for i, alpha in enumerate(alphas):
        if abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.show()


# 函数说明:计算w
# dataMat - 数据矩阵
# labelMat - 数据标签
# alphas - alphas值
# Returns:无
def get_w(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
    w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
    return w.tolist()

#测试
dataMat, labelMat = loadDataSet('testSet.txt')
b,alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
w = get_w(dataMat, labelMat, alphas)
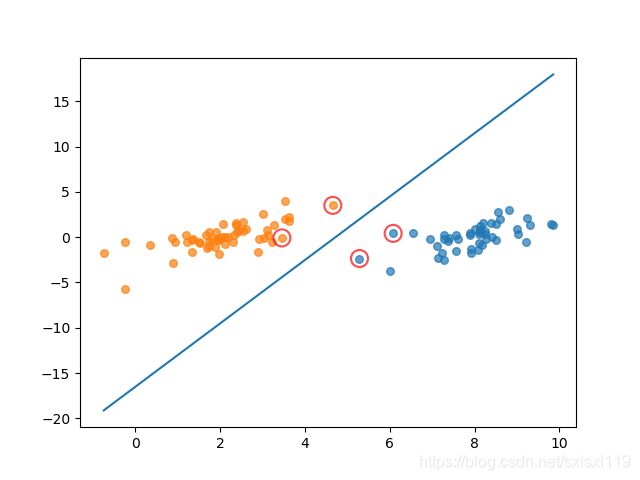
showClassifer(dataMat, w, b)

 代码结果：

 其中，中间的蓝线为求出来的分类器，用红圈圈出的点为支持向量点。

四，SVM实例：手写识别问题

       尽管KNN也能取得不错的效果；但是从节省内存的角度出发，显然SVM算法更胜一筹，因为其不需要保存整个数据集，而只需要起作用的支持向量点，分类效果也不错。

#实例：手写识别问题
#支持向量机由于只需要保存支持向量，所以相对于KNN保存整个数据集占用更少内存
#且取得可比的效果

#基于svm的手写数字识别
def loadImages(dirName):
    from os import listdir
    hwLabels=[]
    trainingFileList=listdir(dirName)
    m=len(trainingFileList)
    trainingMat=zeros((m,1024))
    for i in range(m):
        fileNameStr=trainingFileList[i]
        fileStr=fileNameStr.split('.')[0]
        classNumStr=int(fileStr.split('_')[0])
        if classNumStr==9:hwLabels.append(-1)
        else:hwLabels.append(1)
        trainingMat[i,:]=img2vector('%s/%s',%(dirName,fileNameStr))
    return hwLabels,trainingMat

#将图像转为向量
def img2vector(fileaddir):
    featVec=zeros((1,1024))
    fr=open(filename)
    for i in range(32):
        lineStr=fr.readline()
        for j in range(32):
            featVec[0,32*i+j]=int(lineStr[j])
    return featVec
    
#利用svm测试数字
def testDigits(kTup=('rbf',10)):
    #训练集
    dataArr,labelArr=loadDataSet('trainingDigits')
    b,alphas=smoP(dataArr,labelArr,200,0.0001,10000,kTup)
    dataMat=mat(dataArr);labelMat=mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=dataMat[svInd]
    labelSV=labelMat[svInd]
    print("there are %d Support Vectors",%shape(sVs)[0])
    m,n=shape(dataMat)
    errorCount=0
    for i in range(m):
        kernelEval=kernelTrans(sVs,dataMat[i,:],kTup)
        predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
        if sign(predict)!=sign(labelArr[i]):errorCount+=1
    print("the training error rate is: %f",%(float(errorCount)/m))
    #测试集
    dataArr,labelArr=loadDataSet('testDigits.txt')
    dataMat=mat(dataArr);labelMat=mat(labelArr).transpose()
    errorCount=0
    m,n=shape(dataMat)
    for i in range(m):
        kernelEval=kernelTrans(sVs,dataMat[i,:],('rbf',k1))
        predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
        if sign(predict)!=sign(labelArr[i]):errorCount+=1
    print("the training error rate is: %f",%(float(errorCount)/m))

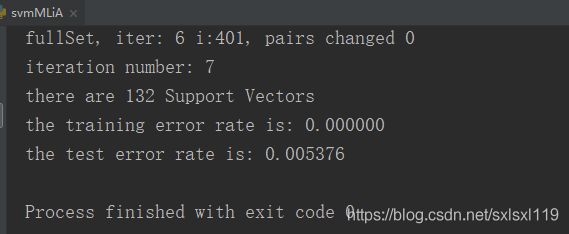
#测试
testDigits(kTup=('rbf', 10))

代码结果：

欢迎扫码关注我的微信公众号