题目描述
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
示例 1:
输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = truncate(3.33333..) = truncate(3) = 3
示例 2:
输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = truncate(-2.33333..) = -2
解题思路
首先要考虑到数字的正负问题,如果除数和被除数都为正数或者都为负数,结果也是正数,否则为负数。使用 sign 标记正负,然后将除数和被除数都转成正数:
int sign = 1;
if ((dividend > 0 && divisor < 0) || (dividend < 0 && divisor > 0)) {
sign = -1;
}
int dividends = Math.abs(dividend);
int divisors = Math.abs(divisor);要求不能使用乘法、除法和取余运算,算出两数相除的值,结果值取整。涉及到运算,那就得使用到别的运算符,比如加法。比如 10/3 转成 10 一直减 3,直到被减的数小于被除数。
10 - 3 = 7
7 -3 = 4
4 - 3 = 1 < 3 上面一共减了三次,所以 10/3 = 3,根据思路写出下面代码:
public int divide(int dividend, int divisor) {
int sign = 1;
if ((dividend > 0 && divisor < 0) || (dividend < 0 && divisor > 0)) {
sign = -1;
}
int dividends = Math.abs(dividend);
int divisors = Math.abs(divisor);
int index = 0;
while (dividends >= divisors) {
dividends = dividends - divisors;
index++;
}
return index * sign;
}
这里涉及到数字范围的问题,我们发现 -2147483648,取相反数还是-2147483648,这是由于编码 int 占四个字节,一个字节八个位。
所以需要使用转成 long 类型,避免数据越界问题:
int sign = 1;
if ((dividend > 0 && divisor < 0) || (dividend < 0 && divisor > 0)) {
sign = -1;
}
long dividends = Math.abs((long) dividend);
long divisors = Math.abs((long) divisor);
long index = 0;
while (dividends >= divisors) {
dividends = dividends - divisors;
index++;
}
if (index > Integer.MAX_VALUE && sign == 1) {
return Integer.MAX_VALUE * sign;
}
return (int) index * sign;结果超时,是因为一个个减,是需要重复次数,时间复杂度是O(n)。
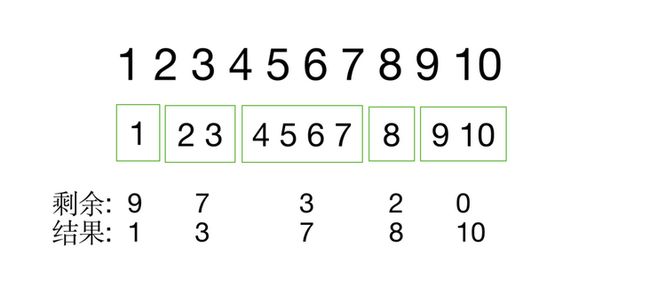
这里需要使用递进式的减法,比如
10/1 = 10
10 - 1 = 9 index = 1
9 - 1 = 8 index = 2
8 - 1 = 7 index = 3
7 - 1 = 6 index = 4
6 - 1 = 5 index = 5
....
1 - 1 = 0 index = 10这上面是要进行十步操作,需要做的一个递进的操作,被除数做加倍,比如上面可以转成:
10 - 1= 9 index = 1 = 1
9 - 1*2 = 7 index = 1 + 1*2 = 3
7 - 1*2*2 = 3 index = 1 + 1*2 + 1 *2*2 = 7
再匹配 3 - 1*2*2*2 < 0,还需要再进行上面的减操作
3 - 1 = 2 index = 7 + 1 = 8
2 - 1*2 = 0 index = 7 + 1 + 1* 2 = 10
根据以上思路可得如下代码:
int sign = 1;
if ((dividend > 0 && divisor < 0) || (dividend < 0 && divisor > 0)) {
sign = -1;
}
long dividends = Math.abs((long) dividend);
long divisors = Math.abs((long) divisor);
long index = 0;
while (dividends >= divisors) {
long temp = divisors;
long i = 1;
while (dividends >= temp) {
dividends = dividends - temp;
index = index + i;
temp = temp << 1;
i = i << 1;
}
}
if (index > Integer.MAX_VALUE && sign == 1) {
return Integer.MAX_VALUE * sign;
}
return (int) index * sign;总结
- 此题解法开始想到将除法转成减法,一个一个累计减
- 需要考虑 int 范围溢出问题,这里统一换成
long类型 - 累减需要的时间负复杂度是O(n),容易超时,这里需要转成递进减法,即每次都对被减数加倍
如果觉得文章对你有帮助的话,请点个赞吧!