狠补基础-数学+算法角度讲解卷积层,激活函数,池化层,Dropout层,BN层,全链接层

狠补基础-数学+算法角度讲解卷积层,激活函数,池化层,Dropout层,BN层,全链接层

在这篇文章中您将会从数学和算法两个角度去重新温习一下卷积层,激活函数,池化层,Dropout层,BN层,全链接层，为您以后修改架构或者自己调试模型提供便利。

卷积层

卷积本是分析数学中的一种运算,在深度学习中使用的卷积运算通常是离散的。作为卷积神经网络中最基础的组成部分,卷积的本质是用卷积核的参数来提取数据的特征,通
过矩阵点乘运算与求和运算来得到结果
如图所示为一个基本二维卷积的运算过程,公式为y=ax+b。这里的特征图(x)大小为1×5×5,即输入通道数为1,卷积核(ω)的大小为3×3,偏置(b)为1,为保证输出维度和输入特征维度一致,还需要有填充( padding),这里使用 zero-padding,即用0来填充。

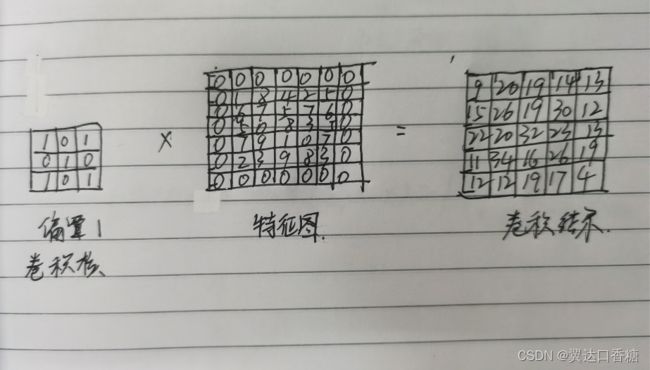
卷积核参数与对应位置像素逐位相乘后累加作为一次计算结果。以图3.3左上角为例,其计算过程为1×0+0×0+1×0+0×0+1×1+0×8+1×0+0×6+1×7+1=9,然后在特征图上进行滑动,即可得到所有的计算结果。

在 Pytorch中使用卷积非常简单,接下来从代码角度介绍如何完成卷积操作。

from torch import nn
#使用 torch.nn中的Conv2d()搭建卷积层 > 
conv=nn.Conv2d(in_channels=1,out_channels=1,kernel_size=3,stride=1,padding=1,dilation=1,groups=1,bias=True)
#查看卷积核的基本信息,本质上是一个 Module
conv
#输入特征图，需要注意的特征必须是四维的，第一维作为batch数，即使是1要保留
input=torch.ones(1,1,5,5)
output=conv(input)
output.shape

对于 torch.mn.onv2d()来说,传入的参数含义如下:
in_channels:输入特征图的通道数,如果是RGB图像,则通道数为3。卷积中的特征图通道数一般是2的整数次幂
out_channels:输出特征图的通道数。
kernel_size:卷积核的尺寸,常见的有1、
stride:步长,即卷积核在特征图上滑动的步长,一般为1。如果大于1,则输出特征图的尺寸会小于输入特征图的尺寸。
padding:填充,常见的有零填充、边缘填充等, Py Torch默认为零填充
dilation:空洞卷积,当大于1时可以增大感受野的同时保持特征图的尺寸,默认为1
groups:可实现组卷积,即在卷积操作时不是逐点卷积,而是将输入通道分为多个组,稀疏连接达到降低计算量的目的,默认为1
bias:是否需要偏置,默认为True

激活函数层

神经网络如果仅仅是由线性的卷积运算堆叠组成,则其无法形成复杂的表达空间,很难提取出高语义的信息,因此还需要加入非线性的映射,又称为激活函数,可以逼近任意的非线性函数,以提升整个神经网络的表达能力。在物体检测任务中,常用的激活函数有 Sigmoid、ReLU及 Softmax函数

Sigmoid函数

Sigmoid型函数又称为 Logistic函数,模拟了生物的神经元特性,即当神经元获得的输入信号累计超过一定的阈值后,神经元被激活而处于兴奋状态,否则处于抑制状态。其函数表达如式所示。
Sigmoid函数曲线与梯度曲线如图，可以看到，Sigmoid函数将特征压缩到了(0,1)区间,0端对应抑制状态,而1对应激活状态,中间部分梯度较大

Pytorch实现 Sigmoid函数很简单,示例如

import torch 
from torch import nn
input=torch.ones(1,1,2,2)
input 

sigmoid=nn.Sigmoid()
sigmoid(input)

Sigmoid函数可以用来做二分类,但其计算量较大,并且容易出现梯度消失现象。从曲线图(图34)中可以看出,在 Sigmoid函数两侧的特征导数接近于0,这将导致在梯度反传时损失的误差难以传递到前面的网络层(因为根据链式求导,梯度接近于0)。

ReLU函数

为了缓解梯度消失现象,修正线性单元( Rectified Linear Unit,ReLU)被引入到神经网络中。由于其优越的性能与简单优雅的实现,ReLU已经成为目前卷积神经网络中最为常用的激活函数之一。ReLU函数的表达式如式所示。
ReLU函数及其梯度曲线如图3.5所示。可以看出,在小于0的部分,值与梯度皆为0,而在大于0的部分中导数保持为1,避免了 Sigmoid函数中梯度接近于0导致的梯度消失。

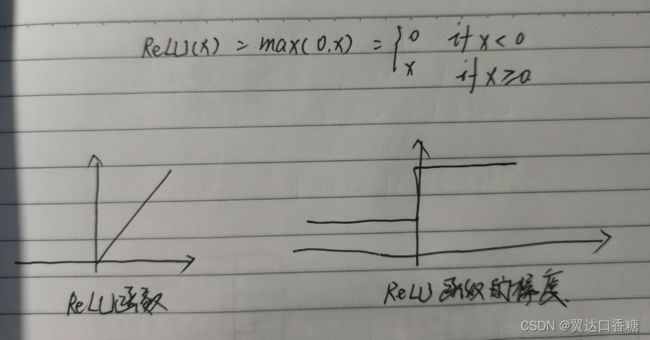
下面是 Pytorch实现ReLU激活函数示例。

relu=nn.ReLU(inplace=True)
relu(input)

ReLU函数计算简单,收敛快,并在众多卷积网络中验证了其有效性。

ReLU激活函数虽然高效,但是其将负区间所有的输入都强行置为0, Leaky Relu 函数优化了这一点,在负区间内避免了直接置0,而是赋予很小的权重,其函数表达式如下
以上公式中的a代表权重，即小于0的值被缩小的比例。Leaky ReLU的函数曲线如图所示：

下面用pytorch来实现简单的Leaky ReLU激活函数过程。

leakyrelu=nn.LeakyReLU(0.04,True)
leakyrelu(input)

akyrelu( (input)井从结果看大于0的值保持不变,小于
0的值被以0.04的比例缩小 sor([[[-0.0701,0.1343],
-0.0385,0.0120111

虽然从理论上讲, Leaky Relu函数的使用效果应该要比ReLU函数好,但是从大量实验结果来看并没有看出其效果比ReLU好。此外,对于ReLU函数的变种,除了 LeakyReLU函数之外,还有 Prell和 Rrelu函数等。

Softmax函数

在物体检测中,通常需要面对多物体分类问题,虽然可以使用 Sigmoid函数来构造多二分类器,但比较麻烦,多物体类别较为常用的分类器是 Softmax函数。
在具体的分类任务中, Softmax函数的输入往往是多个类别的得分,输出则是每一个类别对应的概率,所有类别的概率取值都在0~1之间,且和为1。 Softmax函数的表达如式(3-4)所示,其中,V表示第i个类别的得分,C代表分类的类别总数,输出S1为第i个类别的概率。

在 Pytorch中, Softmax函数在 torch.nn. unctional库中,使用方法如下:

import torch.nn.functional as F 
socre=torch.randn(1,4)
F.softmax(socre,1)

池化层

在卷积网络中,通常会在卷积层之间增加池化( Pooling)层,以降低特征图的参数量,提升计算速度,增加感受野,是一种降采样操作。池化是一种较强的先验,可以使模型更关注全局特征而非局部出现的位置,这种降维的过程可以保留一些重要的特征信息,提升容错能力,并且还能在一定程度上起到防止过拟合的作用。
在物体检测中,常用的池化有最大值池化( Max Pooling)与平均值池化( AveragePooling)。池化层有两个主要的输入参数,即核尺寸 kernel size与步长 stride。如图3.7所示为一个核尺寸与步长都为2的最大值池化过程,以左上角为例,9、20、15与26进行最大值池化,保留26。

池化过程示例
下面是 Pytorch对于池化层的实现

max_pooling=nn.MaxPool2d(2,stride=2)
aver_pooling=nn.AvgPool2d(2,stride=2)
input=torch.randn(1,1,4,4)
max_pooling(input)
aver_pooling(input)

Dropout层

在深度学习中，当参数过多而训练样本又比较少时,模型容易产生过拟合现象，具体表现为在训练集上预测准确率高,而在测试集上准确率大幅下降。2012年, Hinton等人提出了 Dropout算法,可以比较有效地缓解过拟合现象的发生,起到一定正则化的效果。
在训练时神经元以P的概率保留,即以1- p的概率停止工作,每次前向传播保留下来的神经元都不同,这样可以使得模型不太依赖于某些局部特征,泛化性能更强。在测试时,为了保证相同的输出期望值,每个参数还要乘以p。当然还有另外一种计算方式称为 Inverted Dropout,即在训练时将保留下的神经元乘以1p,这样测试时就不需要再改变权重。

Dropout与普通网络的对比

至于 Dropout为什么可以防止过拟合,可以从以下3个方面解释。

1. 多模型的平均:不同的固定神经网络会有不同的过拟合,多个取平均则有可能让些相反的拟合抵消掉,而 Dropout每次都是不同的神经元失活,可以看做是多个模型的平均,类似于多数投票取胜的策略。
   2.减少神经元间的依赖:由于两个神经元不一定同时有效,因此减少了特征之间的依赖,迫使网络学习有更为鲁棒的特征,因为神经网络不应该对特定的特征敏感,而应该从众多特征中学习更为共同的规律,这也起到了正则化的效果
   3.生物进化: Dropout类似于性别在生物进化中的角色,物种为了适应环境变化,在繁衍时取雄性和雌性的各一半基因进行组合,这样可以适应更复杂的新环境,避免了单一基因的过拟合,当环境发生变化时也不至于灭绝。在 Pytorch中使用 Dropout非常简单,示例如下:

dropout=nn.Dropout(0.5,inplace=False)
input=torch.randn(2,64,7,7)
dropout(input)

Dropout被广泛应用到全连接层中,一般保留概率设置为0.5,而在较为稀疏的卷积网络中则一般使用下一节将要介绍的BN层来正则化模型,使得训练更稳定。

BN层

为了追求更高的性能,卷积网络被设计得越来越深,然而网络却变得难以训练收敛与调参。原因在于,浅层参数的微弱变化经过多层线性变换与激活函数后会被放大,改变了每一层的输入分布,造成深层的网络需要不断调整以适应这些分布变化,最终导致模型难
以训练收敛 由于网络中参数变化导致的内部节点数据分布发生变化的现象被称做ICS(Internal Covariate Shift)。ICS现象容易使训练过程陷入饱和区,减慢网络的收敛。前面提到的ReLU从激活函数的角度出发,在一定程度上解决了梯度饱和的现象,而2015年提出的BN层,则从改变数据分布的角度避免了参数陷入饱和区。由于BN层优越的性能,其已经是当前卷积网络中的“标配".
BN层首先对每一个 batch的输入特征进行白化操作,即去均值方差过程。假设一个batch的输入数据为x:B={x1,…xm},首先求该 batch数据的均值与方差,如式所示

以上公式中,m代表 batch的大小,μB为批处理数据的均值,o为批处理数据的方差。在求得均值方差后,利用式进行去均值方差操作

白化操作可以使输入的特征分布具有相同的均值与方差,固定了每一层的输入分布从而加速网络的收敛。然而,白化操作虽然从一定程度上避免了梯度饱和,但也限制了网络中数据的表达能力,浅层学到的参数信息会被白化操作屏蔽掉,因此,BN层在白化操作后又增加了一个线性变换操作,让数据尽可能地恢复本身的表达能力,如所示

公式中,y与B为新引进的可学习参数,最终的输出为y
BN层可以看做是增加了线性变换的白化操作,在实际工程中被证明了能够缓解神经网络难以训练的问题。BN层的优点主要有以下3点
缓解了梯度消失问题。此外,由于每一层数据的均值与方差都在一定范围内,深层 缓解梯度消失,加速网络收敛。BN层可以让激活函数的输入数据落在非饱和区网络不必去不断适应浅层网络输入的变化,实现了层间解耦,允许每一层独立学习也加快了网络的收敛。

简化调参,网络更稳定。在调参时,学习率调得过大容易出现震荡与不收敛,BN层则抑制了参数微小变化随网络加深而被放大的问题,因此对于参数变化的适应能力更强,更容易调参。

防止过拟合。BN层将每一个 batch的均值与方差引入到网络中,由于每个 batch的这两个值都不相同,可看做为训练过程增加了随机噪音,可以起到一定的正则效果,防止过拟合。

在测试时,由于是对单个样本进行测试,没有 batch的均值与方差,通常做法是在训练时将一个 batch的均值与方差都保留下来,在测试时使用所有训练样本均值与方差的平均值。
Py Torch中使用BN层很简单,示例如下:

bn=nn.BatchNorm2d(64)
bn(input)

尽管BN层取得了巨大的成功,但仍有一定的弊端,主要体现在以下两点:
由于是在 batch的维度进行归一化,BN层要求较大的 batch才能有效地工作,而物体检测等任务由于占用内存较高,限制了 batch的大小,这会限制BN层有效地发挥归一化功能。
数据的 batch大小在训练与测试时往往不一样。在训练时一般采用滑动来计算平均值与方差,在测试时直接拿训练集的平均值与方差来使用。这种方式会导致测试集依赖于训练集,然而有时训练集与测试集的数据分布并不一致。
因此,我们能不能避开 batch来进行归一化呢?答案是可以的,最新的工作GN( GroupNormalization)从通道方向计算均值与方差,使用更为灵活有效,避开了 batch大小对归化的影响。
具体来讲,GN先将特征图的通道分为很多个组,对每一个组内的参数做归一化,而不是 batch。GN之所以能够工作的原因,笔者认为是在特征图中,不同的通道代表了不同的意义,例如形状、边缘和纹理等,这些不同的通道并不是完全独立地分布,而是可以放到一起进行归一化分析。

全连接层

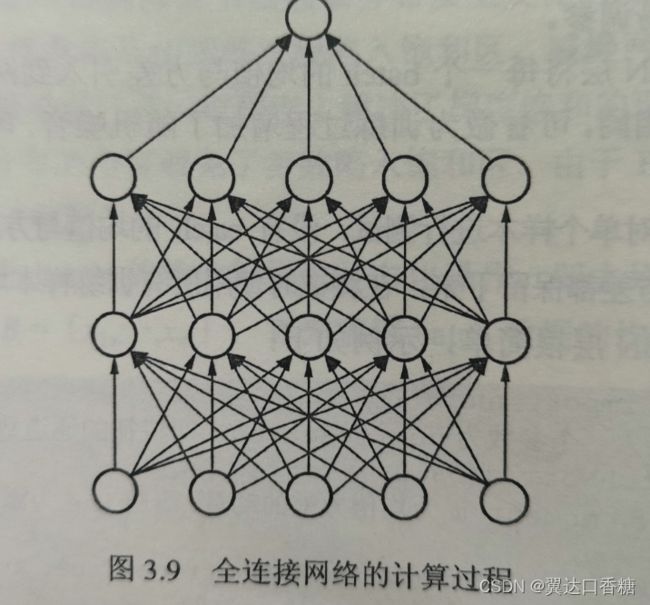
全连接层( (Fully Connected Layers)一般连接到卷积网络输出的特征图后边,特点是每一个节点都与上下层的所有节点相连,输入与输出都被延展成一维向量,因此从参数量 篇物体检测基础知识来看全连接层的参数量是最多的,如图所示。

全连接网络的计算过程
在物体检测算法中,卷积网络的主要作用是从局部到整体地提取图像的特征,而全连接层则用来将卷积抽象出的特征图进一步映射到特定维度的标签空间,以求取损失或者输出预测结果。
在第2章中的感知机例子即是使用了三层的全连接网络进行分类, Pytorch使用全连接层需要指定输入的与输出的维度。示例如下:

linear=nn.linear(1024,4096)
output=linear(input)

然而,随着深度学习算法的发展,全连接层的缺点也逐渐暴露了出来,最致命的问题在于其参数量的庞大。在此以 Vggnet为例说明,其第一个全连接层的输入特征为7×7×512=25088个节点,输出特征是大小为4096的一维向量,由于输出层的每一个点都来自于上一层所有点的权重相加,因此这一层的参数量为25088×4096≈108。相比之下, Vggnet最后一个卷积层的卷积核大小为3×3×512×512≈2.4×106,全连接层的参数量是这一个卷积层的40多倍。
大量的参数会导致网络模型应用部署困难,并且其中存在着大量的参数冗余,也容易发生过拟合的现象在很多场景中,我们可以使用全局平均池化层( Global Average Pooling，GAP）
总体来说，GAP有如下三种好处：

1、利用池化实现了降维，极大地减少了网络的参数量。
2、将特征提取与分类合二为一，一定程度上可以防止过拟合。
3、由于去除了全链接层，可以实现任意图像尺度的输入。