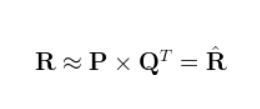python实现推荐系统矩阵分解（Matrix Factorization）提取特征向量

---

前言

矩阵分解是推荐系统中常用的方法，其目的是提取用户的特征向量，以及被打分推荐物品的特征向量。相当于一中embedding的方法，适用于用户极多，被推荐物体数量极大，导致的由于矩阵中存在较多空缺而无法进行推荐的情况。

---

一、Matrix Decomposition数学原理

R为原始矩阵，P和Q使我们要通过学习得到的矩阵，最终P*Q的结果即为我们对于R中空缺值填入后的结果。

加上正则化的LOSS损失函数表达式如上所示，r为原始矩阵的元素，β为正则化系数。在这里我们通过反向传播（Backward Propagation）进行学习，损失函数的偏导数如下。

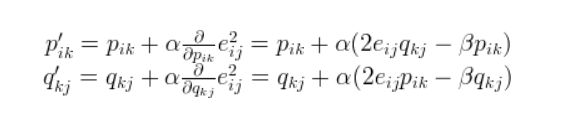
α为学习率（learning rate），这里偏导数并不难求，通过对上面的损失函数手推即可退出。
得到损失函数以及偏导数后我们就可以编程实现了。

二、python实现

程序如下所示：

需要十分注意的是，该算法的核心就是用原始矩阵中真正有用户打分的元素的值，填充特征矩阵，生成预测矩阵。而非用预测矩阵逼近原始矩阵！！！所以必须通过判断原始矩阵在某处是否有值，若有值则通过该值进行梯度下降更新特征值矩阵，若没有则不更新（注意！）。由于numpy中没有只运算有值处元素的API，因此只能通过遍历进行。

**

实际应用中应注意

**

由于我用来提取轨迹中用户的特征因此原始矩阵较大，需要注意的矩阵越大，越要调低learning rate，否则可能出现不收敛的情况。

对于K的选取，K越低最低损失自然也是越大，由于存在大量空值，预测矩阵对这些空值进行了填值，因此评价损失还应该用原始矩阵中存在的值来进行。

import numpy as np
import matplotlib.pyplot as plt
import time

def LOSS(matrix1,matrix2):
    return sum(sum((matrix1-matrix2)**2))**0.5 

def gradiantdecentMD(matrix,K,learningrate,regularate,epoch):
    los=[]
    m1=np.random.rand(matrix.shape[0],K)
    m2 = np.random.rand(matrix.shape[1], K)
    for ep in range(epoch):
        print(ep)
        predict=np.dot(m1,m2.T)
        for i in range(m1.shape[0]):
            for j in range(m2.shape[0]):
                    if matrix[i][j]!=0:
                    lo = loss(true=matrix, m1=m1, m2=m2, i=i, j=j)
                    for k in range(K):
                        m1[i][k] = m1[i][k] + learningrate * (2 * lo * m2[j][k] - regularate * m1[i][k])
                        m2[j][k] = m2[j][k] + learningrate * (2 * lo * m1[i][k] - regularate * m2[j][k])

        los.append(LOSS(predict,matrix))
        print(LOSS(predict,matrix))

        if ep>10:
            if los[-5] - los[-1]<10:
                break

    plt.plot(range(los.__len__()), los)
    plt.show()
    return m1,m2




def main():


    K=10
    epoch=50000
    regularrate=0.01
    learningrate=0.001
    test=np.array([ [5, 3, 0, 1],
                    [4, 0, 0, 1],
                    [1, 0, 0, 4],
                    [0, 1, 5, 4],
                    [0, 1, 5, 4]])


    t1 = time.time()
    userfeature, itemfeature = gradiantdecentMD(test, K, learningrate, regularrate, epoch)
    t2 = time.time()
    print(t2 - t1)
    print(np.dot(userfeature,itemfeature.T))
    np.savetxt(fname='data/userfeature_1000.txt', X=userfeature)
    np.savetxt(fname='data/itemfeature_1000.txt', X=itemfeature)



if __name__ == '__main__':
    main()

总结

总之用于对大量含有空值的矩阵进行学习，与Node2Vec相比无需构成网络，在使用数据填充原始矩阵时也需要一定的方法，才能使原始矩阵更容易被学习，学习效果更好。

http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/#source-code