python 计算离散点的微分和积分(超详细)

前言：

        本文计算离散点微分和积分的内容，参考的是origin软件提供的算法。

        鉴于在百度和谷歌搜索标题的结果不尽人意，因此想在此做一个详细的总结。

        若阅读时间有限，可直接阅读第二或第三部分的代码及其运行结果。

        若有疑问或者错误，欢迎评论区留言提问或者指正，谢谢。

一、原理解释

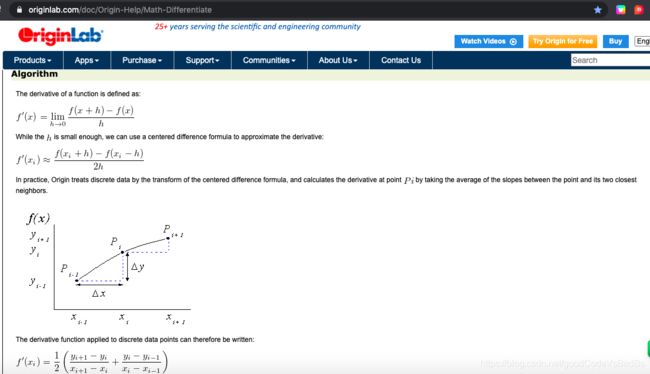
【微分部分】

  大致含义：对于端点以外的散点，其导数为：与其相邻两点的斜率的平均值；                                而位于端点的散点，其导数为：与其最近一点的斜率。

Origin软件中离散点导数的计算公式

【积分部分】

大致含义：两点之间的积分，为两点连线，和两点对x轴的垂线，以及两垂足之间的线段所组成的梯形的面积。本文咱不探讨存在水平线baseline的情况下散点积分的数学面积（面积可正可负）与绝对面积（恒为正），感兴趣的读者可以点击参考文献4去阅读。

 

Origin软件中离散点积分的计算公式

注解：

1.梯形面积公式 = 1/2 * (上底+下底) * 高

2.x(i+1) - x(i)（含有i的括号内的式子均为下标）：表示梯形的高

3.f(x(i+1))+f(x(i))（含有i的括号内的式子均为下标）：表示梯形上下底之和

 

二、纯代码：

【微分部分】

# 定义计算离散点导数的函数
def cal_deriv(x, y):                  # x, y的类型均为列表
    diff_x = []                       # 用来存储x列表中的两数之差
    for i, j in zip(x[0::], x[1::]):  
        diff_x.append(j - i)
 
    diff_y = []                       # 用来存储y列表中的两数之差
    for i, j in zip(y[0::], y[1::]):
        diff_y.append(j - i)  
        
    slopes = []                       # 用来存储斜率
    for i in range(len(diff_y)):
        slopes.append(diff_y[i] / diff_x[i])
        
    deriv = []                        # 用来存储一阶导数
    for i, j in zip(slopes[0::], slopes[1::]):        
        deriv.append((0.5 * (i + j))) # 根据离散点导数的定义，计算并存储结果
    deriv.insert(0, slopes[0])        # (左)端点的导数即为与其最近点的斜率
    deriv.append(slopes[-1])          # (右)端点的导数即为与其最近点的斜率

    for i in deriv:                   # 打印结果，方便检查，调用时也可注释掉
        print(i)

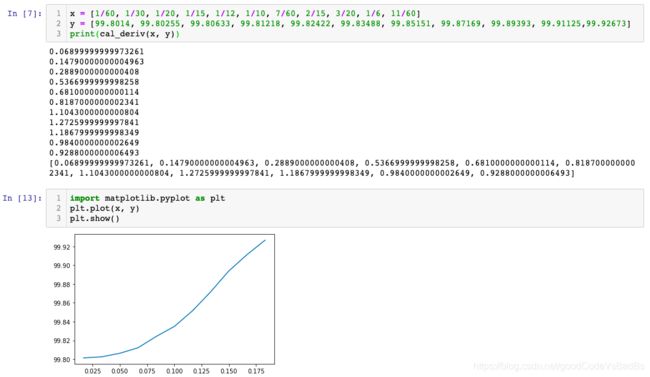
    return deriv                      # 返回存储一阶导数结果的列表

x = [1/60, 1/30, 1/20, 1/15, 1/12, 1/10, 7/60, 2/15, 3/20, 1/6, 11/60]
y = [99.8014, 99.80255, 99.80633, 99.81218, 99.82422, 99.83488, 99.85151, 99.87169, 99.89393, 99.91125,99.92673]

print(cal_deriv(x, y))

# 运行结果
# 0.06899999999973261
# 0.14790000000004963
# 0.2889000000000408
# 0.5366999999998258
# 0.6810000000000114
# 0.8187000000002341
# 1.1043000000000804
# 1.2725999999997841
# 1.1867999999998349
# 0.9840000000002649
# 0.9288000000006493
# [0.06899999999973261, 0.14790000000004963, 0.2889000000000408, 0.5366999999998258, 0.6810000000000114, 0.8187000000002341, 1.1043000000000804, 1.2725999999997841, 1.1867999999998349, 0.9840000000002649, 0.9288000000006493]

为便于理解，展示手算 "x=1/60" 和 "x=1/30" 处(一阶)导数的过程：

x = 1/60:

diff_x = 1/30 - 1/60 = 1/60

diff_y = 99.80255 - 99.8014 = 0.00115

点 "x = 1/60" (端点) 与其相邻点的斜率为：slopes = diff_y / diff_x = 0.00115 / (1/60) = 0.069

点 "x=1/60" 处的导数为：deriv(x = 1/60) = 0.069 (也可0.5 * (0.069+0.069) = 0.069)

 

x = 1/30:

diff_x = 1/20 - 1/30 = 1/60 (由于x的间距均为1/60，因此也可不重复计算)

diff_y = [99.80255 - 99.8014, 99.80633 - 99.80255] = [0.00115, 0.00378]

点 "x = 1/30" 与其相邻两点的斜率分别为：

slopes = [0.00115 / (1/60), 0.00378 / (1/60)] = [0.069, 0.2268]

点 "x=1/30" 处的导数为：deriv(x = 1/30) = 0.5 * ( 0.2268 + 0.069) = 0.1479

注意：设列表x和y的元素个数都为n，则存储两两之差结果的列表diff_x和diff_y的元素个数均为n-1，slopes的元素个数也为n-1；在对deriv进行insert和append操作之前，deriv的元素个数为n-2(原因是对slopes计算两两平均)。为了方便计算，在deriv的两端插入slopes的两端值，这样并不影响结果的正确性(本身+本身的和乘以0.5还是等于本身)。

【微分部分：补充计算二阶导数的函数】

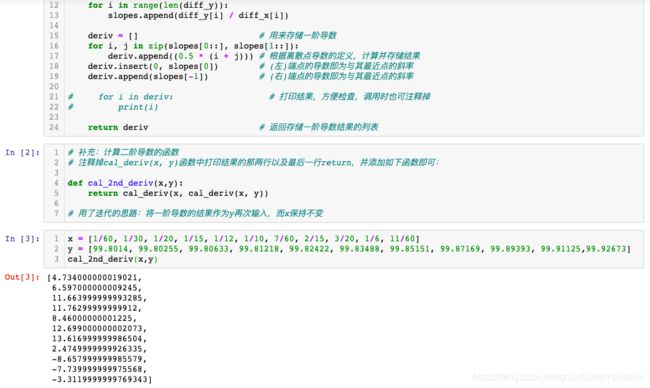
# 补充：计算二阶导数的函数
# 注释掉cal_deriv(x, y)函数中打印结果的那两行以及最后一行return，并添加如下函数即可：

def cal_2nd_deriv(x,y):
    return cal_deriv(x, cal_deriv(x, y))

# 用了迭代的思路：将一阶导数的结果作为y再次输入，而x保持不变

x = [1/60, 1/30, 1/20, 1/15, 1/12, 1/10, 7/60, 2/15, 3/20, 1/6, 11/60]
y = [99.8014, 99.80255, 99.80633, 99.81218, 99.82422, 99.83488, 99.85151, 99.87169, 99.89393, 99.91125,99.92673]
cal_2nd_deriv(x,y)

# 运行结果
# [4.734000000019021,
#  6.597000000009245,
#  11.663999999993285,
#  11.76299999999912,
#  8.46000000001225,
#  12.699000000002073,
#  13.616999999986504,
#  2.4749999999926335,
#  -8.657999999985579,
#  -7.739999999975568,
#  -3.3119999999769343]

为便于理解，展示手算 “x=1/60” 和 “x=1/30” 处二阶导数的过程：

x = 1/60:

diff_x = 1/30 - 1/60 = 1/60

diff_y (diff_deriv) = 0.1479 - 0.069 = 0.0789

点 "x = 1/60" (端点) 与其相邻点的斜率为：slopes = diff_y / diff_x = 0.0789 / (1/60) = 4.734

点 "x=1/60" 处的二阶导数为：2nd_deriv(x = 1/60) = 4.734 (也可0.5 * (4.734 + 4.734) = 4.734)

 

x = 1/30:

diff_x = 1/20 - 1/30 = 1/60 (由于x的间距均为1/60，因此也可不重复计算)

diff_y (diff_deriv) = [0.1479 - 0.069, 0.2889 - 0.1479] = [0.0789, 0.141]

点 "x = 1/30" 与其相邻两点的斜率分别为：

slopes = [0.0789 / (1/60), 0.141 / (1/60)] = [4.734, 8.46]

点 "x=1/30" 处的二阶导数为：2nd_deriv(x = 1/30) = 0.5 * (4.734 + 8.46) = 6.597

【积分部分】

import numpy as np
import scipy
from scipy.integrate import simps # 用于计算积分
import matplotlib.pyplot as plt   # 用于画图

x = np.arange(11)       # 构造一个从0到10的等差数列数组，作为横轴取值
y = np.arange(11)       # 构造一个从0到10的等差数列数组，作为纵轴取值
integrals = []          # 用于存储积分

for i in range(len(y)): # 计算梯形的面积，由于是累加，所以是切片"i+1"
    integrals.append(scipy.integrate.trapz(y[:i + 1], x[:i + 1]))
for i in integrals:     # 输出结果(存储的积分)
    print(i)

plt.plot(x, y)
plt.show()

# 定义计算离散点积分的函数
def cal_integral(x,y):
    import scipy
    from scipy.integrate import simps # 用于计算积分
 
    integrals = []
    for i in range(len(y)): # 计算梯形的面积，由于是累加，所以是切片"i+1"
        integrals.append(scipy.integrate.trapz(y[:i + 1], x[:i + 1]))
    
    return integrals

import numpy as np
x = np.arange(11)       # 构造一个从1到10的等差数列数组，作为横轴取值
y = np.arange(11)       # 构造一个从1到10的等差数列数组，作为纵轴取值

cal_integral(x,y)

# 运行结果
# [0.0, 0.5, 2.0, 4.5, 8.0, 12.5, 18.0, 24.5, 32.0, 40.5, 50.0]

三、代码及其运行结果

【微分部分】

百度经验提供的在Origin软件中计算导数的参考结果

与百度经验提供的参考结果非常接近（精确到小数点后三到四位）

与百度经验提供的参考结果非常接近（精确到小数点后三到四位），以及结果对应的折线图

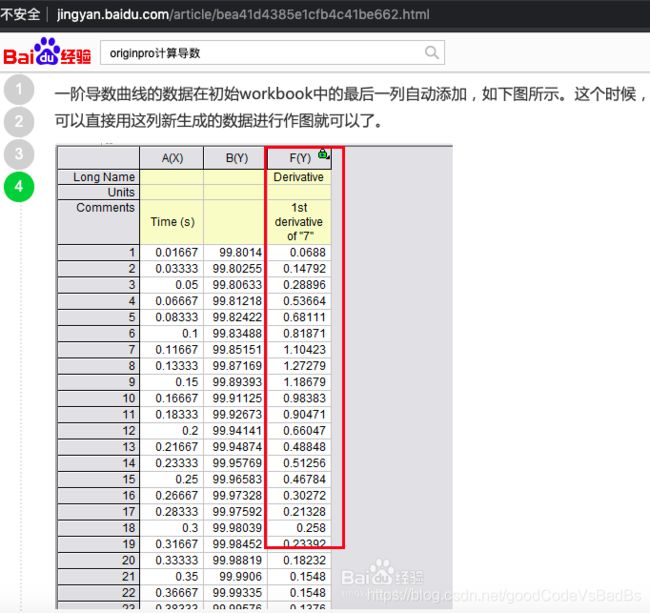
注意：这里的第11个x（11/60）由于处在列表x的末端，其对应的导数不准确（上述结果为0.9288，而实际为0.90471）。这是因为 "x=11/60" 在上述示例中位于右端点，而实际（百度经验中）为非端点。

【微分部分：补充计算二阶导数的函数】

基于导数函数，构造计算二阶导数函数的代码及其运行结果

【积分部分】

函数 "y = x" 在 "x=0" 到 "x=10" 上的积分结果

四、参考文献

【微分部分】

1."Algorithm of calculating derivatives of discrete data in origin software"

2.百度经验：如何使用origin对数据进行一阶求导？

3.Python | Calculate difference between adjacent elements in given list

【积分部分】

4."Algorithm of calculating integrals of discrete data in origin software"

5.Integrating Discrete point in Python

修改记录：

版本号	日期	修改内容
v0.1	2020-08-28	第一版发布
v0.2	2020-09-20	修改了积分部分关于等差数列的小错误: np.arange(10)的"10"改为"11"