python-opencv学习笔记（八）：判断是否雾天与图像能见度测算

引言

本篇是最近碰到的一个关于雾天能见度的问题，然后查阅到很多资料，顺便记录一下思考过程，进行总结归类成笔记。主要参考资料是华为杯2020年E题论文，结合一下自己的实际情况，做出了改进与延伸，文献在最后引出。

相关定义说明

能见度定义：

1. 大气能见度： 能见度是气象、公路行车、飞机飞行中常见指标，单位通常是米。在气象上的能见度定义为：标准视力眼睛观察到水平方向以天空为背景的黑体目标物（0.50）标注为你轮廓的最大水平距离。

2. 雾： 在水汽充足、微风及大气稳定的情况下，相对湿度达到100%时，空气中的水汽便会凝结成细微的水滴悬浮于空中，使地面水平的能见度下降，这种天气现象称为雾。

3. 团雾： 是受局部地区微气候环境的影响，在大雾中数十米到上百米的局部范围内，出现的更“浓”、能见度更低的雾。团雾外视线良好，团雾内一片朦胧。

4. 目标物和背景的亮度对比： 在大气中目标物能见与否，取决于本身亮度，又与它同背景的亮度差异有关。比如，亮度暗的目标物在亮的背景衬托下，清晰可见。或者亮的目标物在暗的背景下，同样清晰可见。表示这种差异的指标是亮度的对比值K。设 为目标物的固有亮度， 为背景的固有亮度，则亮度的对比值定义为：

$$K=\frac{\left|B_0^{\prime }-B_0\right|}{B_0^{\prime }}\text{, if }{B}_0^{\prime }\ge B_0;K=\frac{\left|B_0^{\prime }-B_0\right|}{B_0}\text{, if }{B}_0^{\prime }<B_0$$

5 能见度测量基本方程：
$$F=F_0{e}^{-\sigma z}$$

这里$F$和$F_0$分别表示观测和入射的光照强度，参数$\sigma$称为衰减系数，与雾的厚度有关： $\sigma$越大表明雾越浓。气象光学视程(MOR)

$$\mathrm{MOR}=\frac{\log \left(F/F_0\right)}{-\sigma }=\frac{\log (0.05)}{-\sigma }$$

能见度分级：

高速公路能见度等级划分与影响程度：

等级	能见度 L 范围/m	影响程度
0级	L > 500	-
1级	200	交通预警
2级	100	预警或交通管制
3级	50	交通管制
4级	L < 50	全线或者局部封闭

根据《中华人民共和国气象行业标准》，为了满足高速公路检测场景的服务需求，对雾霾引起的低能见度进行了相应的等级划分，该标准将能见度范围划分为 5 个级别，具体分类如下表所示。当能见度大于 200 米时，即能见度等级为 0 级或 1 级时，高速管理部门无需对车流量和车辆行驶速度进行监管处理，在能见度小于 200 米时，监控人员需要滴交通路况进行管控甚至封路。

是否判断有雾

什么是雾？

在水汽充足、微风及大气稳定的情况下，相对湿度达到100%时，空气中的水汽便会凝结成细微的水滴悬浮于空中，使地面水平的能见度下降，这种天气现象称为雾(Fog)。多出现于春季二至四月间。 形成的条件： 一是冷却，二是加湿，增加水汽含量。 种类有辐射雾、平流雾、混合雾、蒸发雾等。

上面是百度百科中的定义，如果从图片和视频的角度上去分析，雾其实是一种灰色的会让画面产生朦胧感，或者是模糊的一种物质，判断是否有雾的算法是有很多方式，我们可以通过亮度对比，以及基于图像方差或者均值，换种角度，雾气也可以说是一种模糊化产物，那也能通过模糊检测的方式定义这种结构，所以，现在最主流的方法是基于暗通道先验理论，下面将对其分别进行介绍。

图像平均强度

图像强度表示的是单通道图像像素的强度（值的大小），在灰度图像中，它是图像的灰度。在RGB颜色空间中，可以理解把它为是R通道的像素灰度值，G通道的像素灰度值，或是B通道的像素灰度值，也就是RGB中含三个image intensity。

那么我们可以根据在灰度图像中，求出它的平均强度，然后选取相应的阈值来判断是否有雾，并做到筛选或者过滤，基本逻辑为：

im_grey = im.convert('LA')

for i in range(0, width):
    for j in range(0, height):
        total += im.getpixel((i, j))[0]

mean = total / (width * height)

转移到RGB色域，选用120作为强度的阈值，我们可以作为参数进行不断调整：

import os

results = []
for dirpath, dirnames, filenames in os.walk(r"E:\BaiduNetdiskDownload\fog_test"):
    for filenames in [f for f in filenames if f.endswith('.jpg')]:
        # print(dirpath,dirnames,filenames,"......sss")
        filename = os.path.join(dirpath,filenames)
        img = cv2.imread(filename)
        avg_color_per_row = np.average(img, axis=0)
        avg_color = np.average(avg_color_per_row, axis=0)
        results.append(sum(avg_color / 3))
        np_results = np.array(results)
        plt.hist(np_results, bins=100)
        plt.show()

但在我的测试中，以及查询到的资料来看，该方法事实上还是不能很好的过滤有雾和无雾，至少我检测的路面情况来看，两张同样大小的720 * 576的同场景图片，只是一张很明显有雾，一张无，但是results的结果为[128.92051591582342, 122.75210925443668]，所以，我大概估计如果说图片亮度较高，而且颜色比较艳丽突出，我们可以尝试选用图像的平均强度作为衡量标准，不然效果不佳。

那么图片平均强度不行，是否可以选用平均方差呢？

图像方差

**方差（variance) ** 是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。

在图像中，方差是计算每个像元的灰度值减去图像平均灰度值的平方和除以总的像素个数。其实就是将数学中常见的实际抽样问题变成了一张图像关于灰度值的方差问题。而雾其实也算是灰的，那么在实际检测中效果如何呢？我这里选用了四张图片进行方差分析，结果如下：

from PIL import Image
import glob

def slow_horizontal_variance(im):
    '''Return average variance of horizontal lines of a grayscale image'''
    width, height = im.size
    if not width or not height: return 0
    vars = []
    pix = im.load()
    for y in range(height):
        row = [pix[x,y] for x in range(width)]
        mean = sum(row)/width
        variance = sum([(x-mean)**2 for x in row])/width
        vars.append(variance)
    return sum(vars)/height

for fn in glob.glob(r'E:\BaiduNetdiskDownload\qq_test\*.jpg'):
    im = Image.open(fn).convert('L')
    var = slow_horizontal_variance(im)
    fog = var < 200    # FOG THRESHOLD
    print('%5.0f - %5s - %s' % (var, fog and 'FOGGY' or 'SHARP', fn))

图片的水平均值方差结果如下：

Horizontal mean variance is 142	Horizontal mean variance is 504
Horizontal mean variance is 86	Horizontal mean variance is 327

结果上看，效果确实还算不错，比直接做均值是有很明显的提升，但第二幅图和第四幅图感觉还是有点差强人意，这只能说作为一种直接判断灰度的方式，方差有其比较好的地方，但如果雾还没由白转灰，比如上面没有被判定为雾的图片，虽说我阈值设置得比较小，但在我测试其它图片的时候，发现200到300已经算是最能区分雾的情况了。

那么介绍了均值，以及标准差，自然而然一个不得不说的因素是平均梯度，这种也能作为衡量雾气，或者图片模糊等情况的一个指标，这三者的关系是：

• 均值反映了图像的亮度，均值越大说明图像亮度越大，反之越小；
• 标准差反映了图像像素值与均值的离散程度，标准差越大说明图像的质量越好；
• 平均梯度反映了图像的清晰度和纹理变化，平均梯度越大说明图像越清晰；

所以这里，根据网上查找到的资料，使用拉普拉斯算子进行梯度求取。

图像平均梯度

平均梯度有许多种算子供使用，但拉普拉斯算子是最简单的各向同性微分算子，具有旋转不变性。一个二维图像函数的拉普拉斯变换是各向同性的二阶导数，定义为：
$${\nabla }^{2}f(x,y)=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$

在一个二维函数f(x,y)中，x,y两个方向的二阶差分分别为：
$$\begin{array}{rl}& \frac{{\partial }^{2}f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)\\ & \frac{{\partial }^{2}f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y)\end{array}$$

为了更适合于数字图像处理，将该方程表示为离散形式：
$${\nabla }^{2}f=[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)$$

写成filter mask的形式如下：

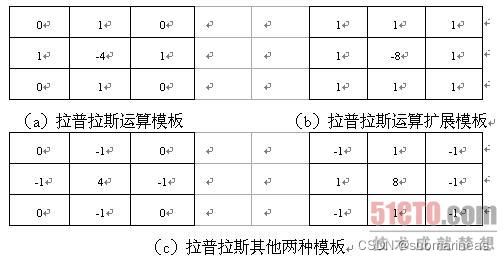
4邻域模板，如果该是8领域方式定义，结果必须必须压四个方向梯度对图像计算，而8领域算法从八个方向梯度对图像进行计算，由此显得图像明亮一点。

这里直接使用opencv中的Laplacian算子，它的一个参数说明如下：

dst = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])
dst 目标图像;
ksize是算子的大小，必须为1、3、5、7。默认为1，即使用的是4邻域模板
scale是缩放导数的比例常数，默认情况下没有伸缩系数；
delta是一个可选的增量，将会加到最终的dst中，同样，默认情况下没有额外的值加到dst中；
borderType是判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。

然后使用这个算子的梯度，鉴别上面方差使用的同一组图片，使用阈值为800，结果如下：

import os, cv2

k = r"E:\BaiduNetdiskDownload\fog_test"

threshold = 800

images = [os.path.join(k, f) for f in os.listdir(k) if f.endswith(".jpg") or f.endswith(".jpeg")]

for image in images:
    img = cv2.imread(image)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
	# blur = cv2.GaussianBlur(gray,(7,7),1,1)  # 核尺寸通过对图像的调节自行定义
    fm = cv2.Laplacian(gray, cv2.CV_64F).var()
    text = "Not Blurry"
    print(fm,"....picture value")
    if fm < threshold:
        text = "Blurry"

        cv2.putText(img, "{}: {:.2f}".format(text, fm), (10, 30),
                    cv2.FONT_HERSHEY_SIMPLEX, 0.8, (0, 0, 255), 3)
        cv2.imshow("Image", img)
        cv2.waitKey(0)
"""
168.8413007482286 ....picture value
109.16813770659722 ....picture value
33.22013163957654 ....picture value
3016.9750480242938 ....picture value
the picture E:\BaiduNetdiskDownload\qq_test\fog2_16.jpeg Laplacian values:168.8413007482286
the picture E:\BaiduNetdiskDownload\qq_test\fog2_18.jpg Laplacian values:109.16813770659722
the picture E:\BaiduNetdiskDownload\qq_test\fog2_29.jpeg Laplacian values:33.22013163957654
"""

这里我跑结果的时候没有加高斯滤波，原因是高斯滤波的sigma比较难设置，如果选的过大，那么会加深滤波程度，这样会导致图像边缘模糊，不利于下一步的边缘检测，我上面设置的核尺寸可以试试，会发现下图本来有接近3000多边缘梯度结果，但是经过滤波后，会得到只有180多的数据，这很明显让阈值的选择更难以区分。而如果滤波值设置得过小，则滤波效果不佳，所以对于这个，干脆不进行了，即使噪声会导致二阶函数产生影响。

阈值设置800以后，只有一张的梯度值为3016，被标记为Not Blurry，上下左边为我打的马赛克，有些标注信息，然后把标注的梯度值放右上角去，非边缘区域有很多雨滴，这种大概率在高斯滤波后会被修正：

对使用Laplacian算子，这种方法凑效的原因就在于拉普拉斯算子定义本身。它被用来测量图片的二阶导数，突出图片中强度快速变化的区域，和 Sobel 以及 Scharr 算子十分相似。并且，和以上算子一样，拉普拉斯算子也经常用于边缘检测。此外，此算法基于以下假设：如果图片具有较高方差，那么它就有较广的频响范围，代表着正常，聚焦准确的图片。但是如果图片具有有较小方差，那么它就有较窄的频响范围，意味着图片中的边缘数量很少。

很显然，此算法的技巧在于设置合适的阈值。然而，阈值却十分依赖于所应用的领域。阈值太低会导致正常图片被误断为模糊图片，阈值太高会导致模糊图片被误判为正常图片。这种方法在能计算出可接受清晰度评价值的范围的环境中趋于发挥作用，能检测出异常照片。

经过上述三种指标的衡量，会发现其各有使用的场景，但作为模糊或者雾的角度分析，其实是递进关系，效果比较好的梯度检测如果在排除其余天气或者说各种噪声干扰，检测效果会要比前两者更好一些。

色彩度对比与图像增强

上述几种方式基本都是直接用的灰度图，这也是目前大部分应用场景都会考虑的，这种指标也比较好量化，而除上述所提到的，判断是否有雾还是有很多方式的，比如下面的灰度直方图就是一种增强局部或者整体的对比度的方法：

灰度直方图是关于灰度级分布的函数，是对图像中灰度级分布的统计。灰度直方图是将数字图像中的所有像素，按照灰度值的大小，统计其出现的频率。灰度直方图是灰度级的函数，它表示图像中具有某种灰度级的像素的个数，反映了图像中某种灰度出现的频率。

映射方法为：
$$s_k=\sum _{j=0}^k\frac{n_j}{n}k=0,1,2,\cdots ,L-1$$

demo如下：

# 绘制图像灰度直方图
def deaw_gray_hist(gray_img):
    '''
    :param  gray_img大小为[h, w]灰度图像
    '''
    # 获取图像大小
    h, w = gray_img.shape
    gray_hist = np.zeros([256])
    for i in range(h):
        for j in range(w):
            gray_hist[gray_img[i][j]] += 1
    x = np.arange(256)
    # 绘制灰度直方图
    plt.bar(x, gray_hist)
    plt.xlabel("gray Label")
    plt.ylabel("number of pixels")
    plt.show()


# 读取图片
img_path = r"E:\BaiduNetdiskDownload\qq_test\fog82.jpg"
img = cv2.imread(img_path)
deaw_gray_hist(img[:,:,0])
cv2.imshow('ori_img', img)
cv2.waitKey()

实际环境中存在着多种因素会影响相机拍摄的图像，为了增强图像的对比度，便于后续提取有效的图像特征信息，可以采用直方图均衡化增强图像的对比度，从灰度直方图中可以看出，原图的灰度分布比较集中：

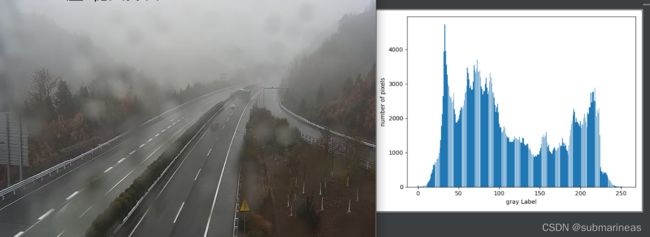
经过直方图均衡化后，我发现确实达到了增强对比度的效果，更容易区分不同灰度间的细节：

但如果拿均衡化后的图片带回原来的算法中，我发现出入就很大了，虽然我感觉就是做了一个归一化，推测原图的有些特征有所缺失，所以虽然说增加了对比度，可以考虑采用新的指标进行区分雾天，或者考虑下面的ACE：

同样，可以根据RGB原色，取出三个通道的一系列值做数据增强，来与原图对比，我感觉这可能也是一种方式来区别：

自动色彩均衡（Automatic Color Enhancement，ACE） 算法是Rizzi大神在Retinex算法的理论上提出的，它通过计算图像目标像素点和周围像素点的明暗程度及其关系来对最终的像素值进行校正，实现图像的对比度调整，产生类似人体视网膜的色彩恒常性和亮度恒常性的均衡，具有很好的图像增强效果。

ACE算法包括两个步骤：

一是对图像进行色彩和空域调整，完成图像的色差校正，得到空域重构图像。
模仿视觉系统的侧抑制性和区域自适应性，进行色彩的空域调整。侧抑制性是一个生理学概念，指在某个神经元受到刺激而产生兴奋时，再刺激相近的神经元，后者所发生的兴奋对前者产生的抑制作用。

二是对校正后的图像进行动态扩展。

对图像的动态范围进行全局调整，并使图像满足灰度世界理论和白斑点假设。算法针对单通道，再延伸应用到RGB彩色空间的3通道图像，即对3个通道分别处理再进行整合完成。

具体的我没有再仔细研究，因为时间问题，感觉上可以进行尝试。这里我不做过多尝试，关于该算法的具体demo以及相关说明，可以参照最底部reference中的图像增强教你去雾一文，这里需要探讨的是另一种算法——暗通道先验算法。

暗通道先验算法

暗通道先验法（Dark Channel Prior，DCR）是何恺明提出的一种突破性的图像去雾算法，经过多次的验证，何恺明总结了在非天空的局部区域中，某一些像素及其周围区域会存在至少一个颜色通道具有很低的值的规律。在实际的计算中，取图像中每个像素点RGB 三通道的最小值，并进行一次最小值滤波，得到暗通道灰度图

Koschmieder 定律已被广泛应用于计算机视觉和图形学领域，表示为如下关系：
$$I(x)=t(x)J(x)+A(1-t(x))$$

$x$表示图像中的像素点，$I(x)$为图像原图，$J(x)$为无雾天气下的清晰图像， $A$为大气光强度值，$t(x)\in [0,1]$表示大气透射率。大气透射率与像素点到摄像机的实际距离$d(x)$和大气消光系数$k$有关，表示为：
$$t(x)=e^{-kd(x)}$$

暗原色先验原理是基于大量户外无雾图像观察到的一条统计规律：在绝大多数户外无雾图像的每个局部区域至少存在某个颜色通道的强度值很低。即对于一幅清晰无雾图像$J$，有：
$$J^{\text{dark }}(X)=\underset{c\in \{r,g,b\}}{\min }\left[\underset{y\in \Omega (x)}{\min }\left(J^C(y)\right)\right]$$

式中，$J^{\text{c}}$ 表示$J$的一个颜色通道，$\Omega (x)$是以$x$为中心的邻域。除了天空区域外，$J^{\text{dark}}$值趋于0，称$J^{\text{dark}}$为$J$的暗通道。在暗原色理论的基础上．求取x 邻域内的透射率。首先假设以x 为中心的邻域内透射率相等，然后对下式两边求取最小值：
$$\frac{{\min }_{c\in \{r,g,b\}}\left[{\min }_{y\in \Omega (x)}\left(I^c(y)\right)\right]}{A}=t(x)\frac{{\min }_{c\in \{r,g,b\}}\left[{\min }_{y\in \Omega (x)}\left(I^c(y)\right)\right]}{A}+(1-t(x))$$

根据暗通道先验知识，无雾图像的暗原色通道趋于 0 的结论，大气环境光有：
$$\underset{c\in \{r,g,b\}}{\min }\left[\underset{y\in \Omega (x)}{\min }\left(J^c(y)\right)\right]=0$$

将上式带入之前的表达式，可以得到透射率为：

$$t(x)=1-\frac{{\min }_{c\in \{r,g,b\}}\left[{\min }_{y\in \Omega (x)}\left(I^c(y)\right)\right]}{A}$$

我们可以根据该公式推算像素值周围的大气透射率，因为大气中或多或少的存在部分的雾霾颗粒，因此需要对上式的计算结果进行限制，通用的做法是在减数项前添加系数$\omega$，并且一般取0.95，得到下式：

$$t(x)=1-\omega \frac{{\min }_{c\in \{r,g,b\}}\left[{\min }_{y\in \Omega (x)}\left(I^c(y)\right)\right]}{A}$$

这样，就得到了透视率。最后能见度求取又回到大气透射率与像素点到摄像机的实际距离$d(x)$和大气消光系数$k$的指数的关系式，可以得到能见度与透射率的关系：
$$k=-\frac{\ln (t(x))}{d(x)}$$

大气消光系数的demo为：

def zmMinFilterGray(src, r=7):
    '''最小值滤波，r是滤波器半径'''
    '''if r <= 0:
        return src
    h, w = src.shape[:2]
    I = src
    res = np.minimum(I  , I[[0]+range(h-1)  , :])
    res = np.minimum(res, I[range(1,h)+[h-1], :])
    I = res
    res = np.minimum(I  , I[:, [0]+range(w-1)])
    res = np.minimum(res, I[:, range(1,w)+[w-1]])
    return zmMinFilterGray(res, r-1)'''
    return cv2.erode(src, np.ones((2 * r + 1, 2 * r + 1)))  # 使用opencv的erode函数更高效


def guidedfilter(I, p, r, eps):
    '''引导滤波，直接参考网上的matlab代码'''
    height, width = I.shape
    m_I = cv2.boxFilter(I, -1, (r, r))
    m_p = cv2.boxFilter(p, -1, (r, r))
    m_Ip = cv2.boxFilter(I * p, -1, (r, r))
    cov_Ip = m_Ip - m_I * m_p

    m_II = cv2.boxFilter(I * I, -1, (r, r))
    var_I = m_II - m_I * m_I

    a = cov_Ip / (var_I + eps)
    b = m_p - a * m_I

    m_a = cv2.boxFilter(a, -1, (r, r))
    m_b = cv2.boxFilter(b, -1, (r, r))
    return m_a * I + m_b


def getV1(m, r, eps, w, maxV1):  # 输入rgb图像，值范围[0,1]
    '''计算大气遮罩图像V1和光照值A, V1 = （1-t）A'''
    V1 = np.min(m, 2)  # 得到暗通道图像
    V1 = guidedfilter(V1, zmMinFilterGray(V1, 7), r, eps)  # 使用引导滤波优化
    bins = 2000
    ht = np.histogram(V1, bins)  # 计算大气光照A
    d = np.cumsum(ht[0]) / float(V1.size)
    for lmax in range(bins - 1, 0, -1):
        if d[lmax] <= 0.999:
            break
    A = np.mean(m, 2)[V1 >= ht[1][lmax]].max()

    V1 = np.minimum(V1 * w, maxV1)  # 对值范围进行限制

    return V1, A


def deHaze(m, r=81, eps=0.001, w=0.95, maxV1=0.80, bGamma=False):
    Y = np.zeros(m.shape)
    V1, A = getV1(m, r, eps, w, maxV1)  # 得到遮罩图像和大气光照
    return V1 , A
    # for k in range(3):
    #     Y[:, :, k] = (m[:, :, k] - V1) / (1 - V1 / A)  # 颜色校正
    # Y = np.clip(Y, 0, 1)
    # if bGamma:
    #     Y = Y ** (np.log(0.5) / np.log(Y.mean()))  # gamma校正,默认不进行该操作
    # return Y


if __name__ == '__main__':
    for i in os.listdir(r"E:\BaiduNetdiskDownload\qq_test"):
        V1, A = deHaze(cv2.imread(fn) / 255.0)
        # print("",fn,A)
        print("picture {0} reflect rate:{1}".format(fn, A))
        # cv2.imwrite('defog.jpg', m)

下面就是求实际距离的过程。

裁剪ROI区域

下图是对100张图做了场差分析后的结果，为了更好地分析图像上不同像素点随时间的变化幅度，根据 100 张图像作了方差计算，发现第 35 张图像出现了一辆车子。可以看见的是公路上出现车会影响整个方差的结果，所以如果说上面的步骤对于排除效果还不是特别好的情况来讲，可以对同一道路上的图片在没有车、树等人为或者环境因素误差下做一个时间性的截图与分析：

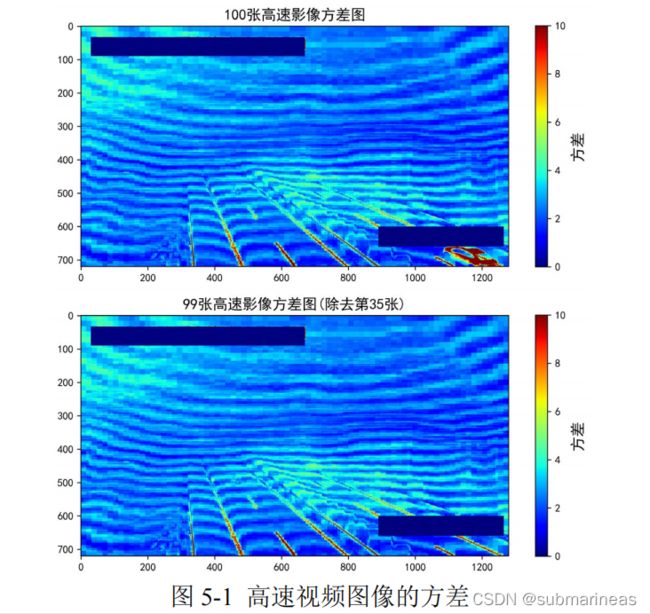
上述图看起来是用MATLAB做的，我感觉上是热力图，但具体咋做的还没研究过，这里是突然看到论文中有提到，那么我顺便引出裁剪ROI：

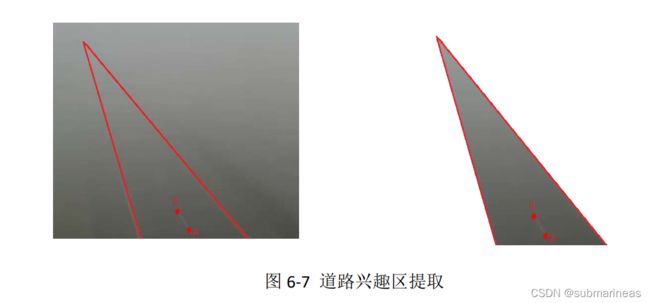
为了消除道路周边建筑物和树木等物体的干扰，后续的能见度检测过程将锁定在道路的区域，利用上述提取的车道线结果，并将其延长至交点，该区域称为道路兴趣区，也就是ROI裁剪。这里我找到了网上一个不规则裁剪的demo：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed May 29 19:18:28 2019
@author: youxinlin
"""
 
import cv2
import numpy as np
 
# -----------------------鼠标操作相关------------------------------------------
lsPointsChoose = []
tpPointsChoose = []
pointsCount = 0
count = 0
pointsMax = 6
def on_mouse(event, x, y, flags, param):
    global img, point1, point2, count, pointsMax
    global lsPointsChoose, tpPointsChoose  # 存入选择的点
    global pointsCount  # 对鼠标按下的点计数
    global img2, ROI_bymouse_flag
    img2 = img.copy()  # 此行代码保证每次都重新再原图画  避免画多了
    # -----------------------------------------------------------
    #    count=count+1
    #    print("callback_count",count)
    # --------------------------------------------------------------
 
    if event == cv2.EVENT_LBUTTONDOWN:  # 左键点击
        pointsCount = pointsCount + 1
        # 感觉这里没有用？2018年8月25日20:06:42
        # 为了保存绘制的区域，画的点稍晚清零
        # if (pointsCount == pointsMax + 1):
        #     pointsCount = 0
        #     tpPointsChoose = []
        print('pointsCount:', pointsCount)
        point1 = (x, y)
        print (x, y)
        # 画出点击的点
        cv2.circle(img2, point1, 10, (0, 255, 0), 2)
 
        # 将选取的点保存到list列表里
        lsPointsChoose.append([x, y])  # 用于转化为darry 提取多边形ROI
        tpPointsChoose.append((x, y))  # 用于画点
        # ----------------------------------------------------------------------
        # 将鼠标选的点用直线连起来
        print(len(tpPointsChoose))
        for i in range(len(tpPointsChoose) - 1):
            print('i', i)
            cv2.line(img2, tpPointsChoose[i], tpPointsChoose[i + 1], (0, 0, 255), 2)
        # ----------------------------------------------------------------------
        # ----------点击到pointMax时可以提取去绘图----------------
 
        cv2.imshow('src', img2)
        
# -------------------------右键按下清除轨迹-----------------------------
    if event == cv2.EVENT_RBUTTONDOWN:  # 右键点击
        print("right-mouse")
        pointsCount = 0
        tpPointsChoose = []
        lsPointsChoose = []
        print(len(tpPointsChoose))
        for i in range(len(tpPointsChoose) - 1):
            print('i', i)
            cv2.line(img2, tpPointsChoose[i], tpPointsChoose[i + 1], (0, 0, 255), 2)
        cv2.imshow('src', img2)
 
    # -------------------------双击 结束选取-----------------------------
    if event == cv2.EVENT_LBUTTONDBLCLK: 
    # -----------绘制感兴趣区域-----------
        ROI_byMouse()
        ROI_bymouse_flag = 1
        lsPointsChoose = []
        
 
def ROI_byMouse():
    global src, ROI, ROI_flag, mask2
    mask = np.zeros(img.shape, np.uint8)
    pts = np.array([lsPointsChoose], np.int32)  # pts是多边形的顶点列表（顶点集）
    pts = pts.reshape((-1, 1, 2))
    # 这里 reshape 的第一个参数为-1, 表明这一维的长度是根据后面的维度的计算出来的。
    # OpenCV中需要先将多边形的顶点坐标变成顶点数×1×2维的矩阵，再来绘制
 
    # --------------画多边形---------------------
    mask = cv2.polylines(mask, [pts], True, (255, 255, 255))
    ##-------------填充多边形---------------------
    mask2 = cv2.fillPoly(mask, [pts], (255, 255, 255))
    cv2.imshow('mask', mask2)
    cv2.imwrite('mask.jpg', mask2)
    image,contours, hierarchy = cv2.findContours(cv2.cvtColor(mask2, cv2.COLOR_BGR2GRAY), cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
    ROIarea = cv2.contourArea(contours[0])
    print("ROIarea:",ROIarea)
    ROI = cv2.bitwise_and(mask2, img)
    cv2.imwrite('ROI.jpg', ROI)
    cv2.imshow('ROI', ROI)
 
img = cv2.imread('3.png')
# ---------------------------------------------------------
# --图像预处理，设置其大小
# height, width = img.shape[:2]
# size = (int(width * 0.3), int(height * 0.3))
# img = cv2.resize(img, size, interpolation=cv2.INTER_AREA)
# ------------------------------------------------------------
ROI = img.copy()
cv2.namedWindow('src')
cv2.setMouseCallback('src', on_mouse)
cv2.imshow('src', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

这个是不依赖输入坐标点，能直接在图像中不按照规则，随机点击各种区域，并且根据点的连线，当双击后会将连线包围后的多边形进行裁剪，截图后背景图层默认为黑：

相机标定理论

本文以高速公路监控图像为研究基础，实际场景为高速公路环境，标定关键点可以结合高速公路固有的路面车道线构造尺寸数据。根据《公路交通安全设施设计细则》对车道分界线线长进行规定，每一条车道分界线的长度为 6m，相邻车道分界线之间的距离为 9m。本文采用车道分界线的数据对摄像机进行标定。在高速公路监控中，可以利用云台转动与变焦功能对摄像机前后一定范围内视频图像采集，确保获取图像中具有车道分界线。

摄像机标定选点示意图如上图所示，其中红色标记为有雾图像中所能看到的最远距离，上端点和下端点之间的距离表示每一条车道分界线的长度，下端点距离相邻车道分界线为车道分界线之间的距离。

后面的推导就不再这里详述，主要是引出一个思想，如果想看中间推导，可以查看参考文献1中的那篇建模论文，这是一种方案，另外一种方案见参考文献2中，直接从视频画面中求得图像的灭点（Vanishing Point，立体图形各条边的延伸线所产生的相交点）。

《高速公路监控技术要求》中指出高速公路上摄像机采用立柱安装，安装高度在 8~12m范围内，因此可利用摄像机坐标与世界坐标关系求解距离深度。而同样是根据国标，车道线一般宽约为 20cm，长度为 6m，间隔为 9m。这对于这里的基于单目图像测算实际距离具有很大帮助。具体的不再这里论述，我也有试验过某篇参考论文中使用的代码，但还是发现有很大问题：

from moviepy.editor import VideoFileClip
import matplotlib.pyplot as plt
import matplotlib.image as mplimg
import numpy as np
import cv2

blur_ksize = 5  
canny_lthreshold = 50  
canny_hthreshold = 150  


rho = 1
theta = np.pi / 180
threshold = 15
min_line_length = 40
max_line_gap = 20

def roi_mask(img, vertices):
  mask = np.zeros_like(img)

  
  if len(img.shape) > 2:
    channel_count = img.shape[2]  
    mask_color = (255,) * channel_count
  else:
    mask_color = 255

  cv2.fillPoly(mask, vertices, mask_color)
  masked_img = cv2.bitwise_and(img, mask)
  return masked_img

def draw_roi(img, vertices):
  cv2.polylines(img, vertices, True, [255, 0, 0], thickness=2)

def draw_lines(img, lines, color=[255, 0, 0], thickness=2):
  for line in lines:
    for x1, y1, x2, y2 in line:
      cv2.line(img, (x1, y1), (x2, y2), color, thickness)

def hough_lines(img, rho, theta, threshold, min_line_len, max_line_gap):
  lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)
  line_img = np.zeros((img.shape[0], img.shape[1], 3), dtype=np.uint8)
  
  draw_lanes(line_img, lines)
  return line_img

def draw_lanes(img, lines, color=[255, 0, 0], thickness=8):
  left_lines, right_lines = [], []
  for line in lines:
    for x1, y1, x2, y2 in line:
      k = (y2 - y1) / (x2 - x1)
      if k < 0:
        left_lines.append(line)
      else:
        right_lines.append(line)
  
  if (len(left_lines) <= 0 or len(right_lines) <= 0):
    return img
  
  clean_lines(left_lines, 0.1)
  clean_lines(right_lines, 0.1)
  left_points = [(x1, y1) for line in left_lines for x1,y1,x2,y2 in line]
  left_points = left_points + [(x2, y2) for line in left_lines for x1,y1,x2,y2 in line]
  right_points = [(x1, y1) for line in right_lines for x1,y1,x2,y2 in line]
  right_points = right_points + [(x2, y2) for line in right_lines for x1,y1,x2,y2 in line]
  
  left_vtx = calc_lane_vertices(left_points, 325, img.shape[0])
  right_vtx = calc_lane_vertices(right_points, 325, img.shape[0])
  
  cv2.line(img, left_vtx[0], left_vtx[1], color, thickness)
  cv2.line(img, right_vtx[0], right_vtx[1], color, thickness)
  
def clean_lines(lines, threshold):
  slope = [(y2 - y1) / (x2 - x1) for line in lines for x1, y1, x2, y2 in line]
  while len(lines) > 0:
    mean = np.mean(slope)
    diff = [abs(s - mean) for s in slope]
    idx = np.argmax(diff)
    if diff[idx] > threshold:
      slope.pop(idx)
      lines.pop(idx)
    else:
      break
  
  
def calc_lane_vertices(point_list, ymin, ymax):
  x = [p[0] for p in point_list]
  y = [p[1] for p in point_list]
  fit = np.polyfit(y, x, 1)
  fit_fn = np.poly1d(fit)
  
  xmin = int(fit_fn(ymin))
  xmax = int(fit_fn(ymax))
  
  return [(xmin, ymin), (xmax, ymax)]

def process_an_image(img):
  roi_vtx = np.array([[(0, img.shape[0]), (460, 325), (520, 325), (img.shape[1], img.shape[0])]])

  gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
  blur_gray = cv2.GaussianBlur(gray, (blur_ksize, blur_ksize), 0, 0)
  edges = cv2.Canny(blur_gray, canny_lthreshold, canny_hthreshold)
  roi_edges = roi_mask(edges, roi_vtx)
  line_img = hough_lines(roi_edges, rho, theta, threshold, min_line_length, max_line_gap)
  res_img = cv2.addWeighted(img, 0.8, line_img, 1, 0)

  '''
  plt.figure()
  plt.imshow(img)
  plt.savefig('images/lane_original.png', bbox_inches='tight')
  plt.figure()
  plt.imshow(gray, cmap='gray')
  plt.savefig('images/gray.png', bbox_inches='tight')
  plt.figure()
  plt.imshow(blur_gray, cmap='gray')
  plt.savefig('images/blur_gray.png', bbox_inches='tight')
  plt.figure()
  plt.imshow(edges, cmap='gray')
  plt.savefig('images/edges.png', bbox_inches='tight')
  plt.figure()
  plt.imshow(roi_edges, cmap='gray')
  plt.savefig('images/roi_edges.png', bbox_inches='tight')
  plt.figure()
  plt.imshow(line_img, cmap='gray')
  plt.savefig('images/line_img.png', bbox_inches='tight')
  plt.figure()
  plt.imshow(res_img)
  plt.savefig('images/res_img.png', bbox_inches='tight')
  plt.show()
  '''

  return res_img
 



output = 'video_2_sol.mp4'
clip = VideoFileClip("video_2.mp4")
out_clip = clip.fl_image(process_an_image)
out_clip.write_videofile(output, audio=False)

上述代码是一个非网络的求取车道线的方法，但好像大部分博客都是拿来做车载视频检测，论文是改成了车道线并加了录制功能来针对摄像头视角，但效果并没有原建模论文提到的那么好，拿了一个非车载视频，并且不是原题给出的视频进行了实验，效果如下：

如果拿华为杯原视频进行检测，我感觉效果也应该差不多，抖动明显，不太好做判断，这里为啥会把上述demo贴出，因为我感觉这个就很好的对我上面内容做了总结，比如感兴趣ROI区域，还有眼膜，阈值。所以目前车道线检测，基本都是用网络了。

分割网络求取车道线

这里还是建议用语义分割网络对车道线进行检测，目前已经有很多比较好的模型了，比如lanenet、unet、deeplab甚至是CondLaneNet，以上这些我尝试了下deeplabv3+mobile net，然后对于1M的码流进行推理，发现也挺快的，作为随机场景下，大概单张图片能达到70ms左右，如果是用上述的非模型方法，一通判断下来时间也延长了很多，并且还不太准确，具体的预测结果如下图：

关于深度学习训练车道线模型的案例，可以直接去deeplab的GitHub，readme写得比较清晰，跟yolo差不多，如果有时间，我会另开一篇专门写这个，那么这里不再过多提，如果按照上图一样，有了车道线，并且线都是汇聚成一点，那么可以根据最大最小值判断拿到那个灭点，而如果没有汇聚成点，知道车的行驶方向，那么可以根据当前方向，同样可以拿到想要的条件，这种准确率会比单纯计算来得要高。

reference

1. 基于深度学习的大雾条件下能见度估计与预测（周尧、郑洁、侯贵洋）（南京审计大学,天津大学,中国科学院大学）
2. 能见度估计与预测（宋智超、刘旗洋、季仁杰）（华东师范大学）
3. 用 Opencv 和 Python 模糊检测
4. 雾霾模糊？图像增强教你如何去雾
5. Foggy images detection [closed]
6. 《CondLaneNet：a Top-to-down Lane Detection Framework Based on Conditional Convolution》论文笔记
7. OpenCV 自学笔记33. 计算图像的均值、标准差和平均梯度
8. python+opencv图像分割：分割不规则ROI区域方法汇总