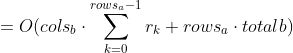【数据结构原理】稀疏矩阵 - THE SPARSE MATRIX

目录

稀疏矩阵（THE SPARSE MATRIX）

0x00 ADT

 0x01 ADT - 稀疏矩阵

0x02 稀疏矩阵的表示

0x03 矩阵的转置 - Transposing A Matrix

0x04 矩阵乘

---

稀疏矩阵（THE SPARSE MATRIX）

0x00 ADT

稀疏矩阵：若矩阵 中 非零元素的个数远小于零元素的个数，我们称  为稀疏矩阵

如果用一个二维数组来表示稀疏矩阵，就要用大量的空间来存储相同的值（0），不仅如此，当矩阵很大时，这种实现方式是行不通的，因为大多数编译器对数组的大小都有限制的。

 0x01 ADT - 稀疏矩阵

0x02 稀疏矩阵的表示

我们可以唯一地表示矩阵中的任何元素，我们可以利用 row，col，value 的方式存储和定位稀疏矩阵中的非零元素，这种存储稀疏矩阵的方式称为三元组 Triple。

by a triple .

我们组织三元组，使行指数按升序排列，在具有相同行指数的三元组中，按列指数的升序排列。

为了确保操作能够停止，我们必须知道行和列的数量，以及矩阵中的非零元素的数量。

// Sparse_Matrix Create(max_row, max_col) ::=

#define Max_TERMS 101 /* maximum number of terms +1*/
typedef struct {
    int col;
    int row;
    int value;
} term;
term a[MAX_TERMS];

0x03 矩阵的转置 - Transposing A Matrix

<一个简单的算法>

对于每一行的 

        取元素  并储存它

        作为转置的元素  

在我们处理完前面的所有元素之前，我们不会确切的知道在转置中吧元素 

放在了哪里，比如：

 需要连续的插入。我们必须移动元素以保持顺序正确。

我们可以通过通过使用列的索引来确定元素在矩阵中的位置，来避免这种数据移动。

对于第  列的所有元素，将元素  放在元素 中。

[Program 2.8]

时间复杂度：  

如果  ， 变为 。

 一个使用密集表示的转置算法

for (j = 0; j < columns; j++)
    for (i = 0; i < rows; i++)
        b[j][i] = a[i][j];

时间复杂度：

通过使用更多一点的存储空间来实现更好的算法

fast_transpose

该算法，首先确定原始矩阵每一列的元素数量。

该数字给出了转置矩阵中每一行的元素数。

时间复杂度：

如果  ，

那么  变为 

使用了额外的数组，row_terms 和 starting_pos 。

如果我们把起始位置放到 row_terms 使用的空间里，我们就可以把空间减少到一个数组。

0x04 矩阵乘法

给出两个矩阵  和 ，其中  是  ， 是 

乘积矩阵  为 ，它的  元素为：

        

<使用密集表示法的矩阵乘法算法>

for (i = 0; i < rows_a; i++) {
    for (j = 0; j < cols_b; j++) {
        sum = 0;
        for (k = 0; k < cols_a; k++)
            sum += a[i][k]*b[k][j];
        d[i][j] = sum;
    }
}

时间复杂度： 

注意，两个稀疏矩阵的乘积可能就不再是稀疏的了。例如：

[Program 2.10]

矩阵  分别存储在数组  中， 的转置存储在 new_b 中。

使用变的变量：

row - 目前正在与B的列相乘的A的行
row_begin - 当前行的第一个元素在a中的位置
column - 目前正在与A的某一行相乘的B的列
totald - 乘积矩阵D的当前元素数
i, j - 用于连续检查A行和B列中的元素的指针

void mmult(term a[], term b[], term d[])
/* multiply two sparse matrices */
{
    int i, j, column, totalb = b[0].value, totald = 0;
    int rows_a = a[0].row, cols_a = a[0].col, totala = a[0].value;
    int cols_b = b[0].col;
    int row_begin = 1, row = a[1].row, sum = 0;

    term new_b[MAX_TERMS];
    if (col_a != b[0].row) {
        fprintf(stderr, “Incompatible matrices\n”);
        exit(1);
    }
    fast_transpose(b, new_b);
    /* set boundary condition */
    a[totala+1].row = rows_a;
    new_b[totalb+1].row = cols_b; new_b[totalb+1].col = -1;
   
    for (i = 1; i <= totala; ) {
        column = new_b[1].row;
        for (j = 1; j <= totalb+1; ) {
        /* multiply row of a by column of b */
            if (a[i].row != row) {
                storesum(d, &totald, row, column, &sum);
                i = row_begin;
                for ( ; new_b[j].row == column; j++)
                                ;
                column = new_b[j].row;
            }
            else if (new_b[j].row != column) {
                storesum(d, &totald, row, column, &sum);
                i = row_begin;
                column = new_b[j].row;
            }
            else switch (COMPARE(a[i].col, new_b[j].col)) {
                case –1 : /* go to next term in a */
                    i++; break;
                case 0 : /* add terms, go to next term in a and b */
                    sum += (a[i++].value * new_b[j++].value);
                    break;
                case 1 : /* go to next term in b */
                    j++;
            }
        } /* end of for j <= totalb+1 */
        for ( ; a[i].row == row; i++)
                ;
        row_begin = i; row = a[i].row;
    } /* end of for i <= totala */
    d[0].row = row_a; d[0].col = cols_b;
    d[0].value = totald;
}

注意，我们在 a 和 new_b 中都引入了一个附加项：

a[totala+1].row = rows_a;
new_b[totalb+1].row = cols_b;
new_b[totalb+1].col = -1;

时间复杂度

for 循环前：

fast transpose - O(cols_b + totalb) time.

外层 for 循环被迭代了rows_a 次：

在每次迭代中，乘积矩阵D的一行由内部 for 循环计算，在每个迭代中，i或者j两者都增加1，或者i被重置到 row_begin

j 的最大总增量为 totalb+1。 那么当第k行被处理时，i最多可以增加几次，i最多被重置到row_begin的cols_b次。 因此，i的最大总增量是cols_b-。 内层for循环需要  时间，列被重置。 因此外部 for 循环需要

值得注意的是，如果  且  ，那么他的时间复杂度会变为  。