高斯滤波器(Gaussian Filter) python实现及部分原理说明（opencv）

上传图片

# read the image
img = cv2.imread("img/11.jpeg")

# Print out the type of image data and its dimensions (height, width, and color)
print('This image is:', type(img), 
      ' with dimensions:', img.shape)

img_copy = np.copy(img)
#change color to rgb(from bgr)
img_copy = cv2.cvtColor(img_copy,cv2.COLOR_BGR2RGB)
 #display
plt.imshow(img_copy)

This image is:   with dimensions: (742, 742, 3)

添加高斯噪声

def noise_Gaussian(img,mean,var):
    '''
    img:原始图像
    mean：均值
    var：方差，值越大噪声越大
    '''
    #创建均值为mean方差为var呈高斯分布的图像矩阵
    noise = np.random.normal(mean,var ** 0.5,img.shape)

    #将原始图像的像素值进行归一化，除以255使像素值在0-1之间
    img = np.array(img/255,dtype=float)

    #噪声和图片合并即加噪后的图像
    out = img + noise
    
    #解除归一化，乘以255将加噪后的图像的像素值恢复
    out = np.uint8(out*255)
    return out

out = noise_Gaussian(img_copy,mean=0,var=0.003)
plt.imshow(out)

高斯滤波器

高斯滤波器将中心像素周围的像素按照高斯分布加权平均进行平滑化。这样的（二维）权值通常被称为卷积核（kernel）或者滤波器（filter）

但是，由于图像的长宽可能不是滤波器大小的整数倍，因此我们需要在图像的边缘补0 。这种方法称作Zero Padding

权值g （卷积核）要进行归一化操作（∑ g = 1 \sum\ g = 1∑ g=1）

高斯掩膜的求解与位置(x,y)无关，因为在计算过程中x,y被抵消掉了,所以求一个kerne模板即可

gaussian_filter算法

对图像进行zero padding
根据高斯滤波器的核大小和标准差大小实现高斯滤波器
使用高斯滤波器对图像进行滤波（相乘再相加）
输出高斯滤波后的图像

gaussian_filter代码示例

def gaussian_filter(img, K_size=3, sigma=1.0):
    img = np.asarray(np.uint8(img))
    if len(img.shape) == 3:
        H, W, C = img.shape
    else:
        img = np.expand_dims(img, axis=-1)
        H, W, C = img.shape
 
    ## Zero padding
    pad = K_size // 2
    out = np.zeros((H + pad * 2, W + pad * 2, C), dtype=np.float)
    out[pad: pad + H, pad: pad + W] = img.copy().astype(np.float)
 
    ## prepare Kernel
    K = np.zeros((K_size, K_size), dtype=np.float)
    for x in range(-pad, -pad + K_size):
        for y in range(-pad, -pad + K_size):
            K[y + pad, x + pad] = np.exp( -(x ** 2 + y ** 2) / (2 * (sigma ** 2)))
    K /= (2 * np.pi * sigma * sigma) 
    K /= K.sum()
    tmp = out.copy()
 
    # filtering
    for y in range(H):
       for x in range(W):
            for c in range(C): 
                out[pad + y, pad + x, c] = np.sum(K * tmp[y: y + K_size, x: x + K_size, c])
    out = np.clip(out, 0, 255)
    out = out[pad: pad + H, pad: pad + W].astype(np.uint8)
    return out

sigma的意义及选取

高斯滤波器模板的生成最重要的参数就是高斯分布的标准差σ。
标准差代表着数据的离散程度，如果σ较小，那么生成的模板的中心系数较大，而周围的系数较小，这样对图像的平滑效果就不是很明显；
反之，σ较大，则生成的模板的各个系数相差就不是很大，比较类似均值模板，对图像的平滑效果比较明显

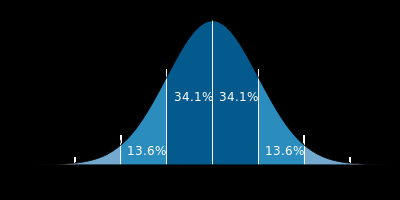
高斯分布的概率分布密度图 ↑
可以看到：σ越小分布越瘦高，σ越大分布越矮胖

不同sigma和k_size结果展示

#sigma=0.5 k_size=3
out_05=gaussian_filter(img_copy,sigma=0.5)
plt.imshow(out_05)

#sigma=0.5 k_size=5
out_05_5=gaussian_filter(img_copy,K_size=5,sigma=0.5)
plt.imshow(out_05_5)

#sigma=0.8 k_size=3
out_08=gaussian_filter(img_copy,sigma=0.8)
plt.imshow(out_08)

#sigma=0.8 k_size=5
out_08_5=gaussian_filter(img_copy,K_size=5,sigma=0.8)
plt.imshow(out_08_5)

#sigma=1.3  k_size=3
out_13=gaussian_filter(img_copy,sigma=1.3)
plt.imshow(out_13)

#sigma=1.3  k_size=5
out_13_5=gaussian_filter(img_copy,K_size=5,sigma=1.3)
plt.imshow(out_13_5)

#sigma=2.0  k_size=3
out_20=gaussian_filter(img_copy,K_size=3,sigma=2.0)
plt.imshow(out_20)

#sigma=2.0  k_size=5
out_20_5=gaussian_filter(img_copy,K_size=5,sigma=2.0)
plt.imshow(out_20_5)

源码地址

https://github.com/Xnhyacinth/xnhyacinth/blob/master/CV/Gaussian%20Filter.py