python机器学习参数调优
前言
此系列文章旨在记录本人学习python过程中遇到的一些值得总结,方便之后及时复习的内容。
本篇博客介绍机器学习中参数调优的一些知识,即网格搜索,随即搜索等,以及一些pipeline的知识。
文章目录
-
-
- 前言
- 基础知识
- 回归问题建模
-
- 数据读取了解
- 简单模型建模
- 参数与超参数
- 参数寻优理论
- pipeline思维
- 参数寻优实战
- 分类问题建模
-
- 参数调优实战
- 混淆矩阵和ROC曲线
- 总结
- 参考文献
-
基础知识
有监督学习中根据因变量的连续与否,可以分为回归和分类问题:
- 回归:因变量是连续型变量,如:房价,体重等。
- 分类:因变量是离散型变量,如:是否患癌症,西瓜是好瓜还是坏瓜等。
为了更好地叙述后面的内容,我们对数据的形式作出如下约定:
第 i i i个样本: x i = ( x i 1 , x i 2 , . . . , x i p , y i ) T , i = 1 , 2 , . . . , N x_i=(x_{i1},x_{i2},...,x_{ip},y_i)^T,i=1,2,...,N xi=(xi1,xi2,...,xip,yi)T,i=1,2,...,N
因变量 y = ( y 1 , y 2 , . . . , y N ) T y=(y_1,y_2,...,y_N)^T y=(y1,y2,...,yN)T
第 k k k个特征: x ( k ) = ( x 1 k , x 2 k , . . . , x N k ) T x^{(k)}=(x_{1k},x_{2k},...,x_{Nk})^T x(k)=(x1k,x2k,...,xNk)T
特征矩阵 X = ( x 1 , x 2 , . . . , x N ) T X=(x_1,x_2,...,x_N)^T X=(x1,x2,...,xN)T
在学习机器学习中,我们经常使用scikit-learn简称sklearn工具库来探索机器学习项目,下面我们开始使用sklearn来进行讲解[1]。。
回归问题建模
数据读取了解
首先,我们先来看看有监督学习中回归的例子,我们使用sklearn内置数据集Iris数据集。sklearn中所有内置数据集都封装在datasets对象内:
返回的对象有:
- data:特征X的矩阵(ndarray)
- target:因变量的向量(ndarray)
- feature_names:特征名称(ndarray)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 在jupyter中通过下行才可方便绘图查看
%matplotlib inline
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
features = iris.feature_names
iris_data = pd.DataFrame(X,columns=features)
iris_data['target'] = y
iris_data.describe()
这里可以进行一个简单的可视化,如:
# 可视化特征
marker = ['s','x','o']
for index,c in enumerate(np.unique(y)):
plt.scatter(x=iris_data.loc[y==c,"sepal length (cm)"],y=iris_data.loc[y==c,"sepal width (cm)"],alpha=0.8,label=c,marker=marker[c])
plt.xlabel("sepal length (cm)")
plt.ylabel("sepal width (cm)")
plt.legend()
plt.show()
简单模型建模
接下来通过线性回归、回归树、支持向量机SVR来进行演示回归问题求解。
- 线性回归
from sklearn import linear_model # 引入线性回归方法
lin_reg = linear_model.LinearRegression() # 创建线性回归的类
lin_reg.fit(X,y) # 输入特征X和因变量y进行训练
print("模型系数:",lin_reg.coef_) # 输出模型的系数
print("模型得分:",lin_reg.score(X,y)) # 输出模型的决定系数R^2
- 回归树
from sklearn import tree
reg_tree = tree.DecisionTreeRegressor(criterion="mse", min_samples_leaf=5)
reg_tree.fit(X,y)
reg_tree.score(X,y)
- 支持向量机
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler # 标准化数据
from sklearn.pipeline import make_pipeline # 使用管道,把预处理和模型形成一个流程
reg_svr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
reg_svr.fit(X, y)
reg_svr.score(X,y)
参数与超参数
- 岭回归补充
岭回归(L2正则化的例子),在线性回归中,我们的损失函数为
J ( w ) = ∑ i = 1 N ( y i − w 0 − ∑ j = 1 p w j x i j ) 2 J(w) = \sum\limits_{i=1}^{N}(y_i-w_0-\sum\limits_{j=1}^{p}w_jx_{ij})^2 J(w)=i=1∑N(yi−w0−j=1∑pwjxij)2
,我们在线性回归的损失函数的基础上添加对系数的约束或者惩罚,即:
J ( w ) = ∑ i = 1 N ( y i − w 0 − ∑ j = 1 p w j x i j ) 2 + λ ∑ j = 1 p w j 2 , 其 中 , λ ≥ 0 w ^ = ( X T X + λ I ) − 1 X T Y J(w) = \sum\limits_{i=1}^{N}(y_i-w_0-\sum\limits_{j=1}^{p}w_jx_{ij})^2 + \lambda\sum\limits_{j=1}^{p}w_j^2,\;\; 其中,\lambda \ge 0\\ \hat{w} = (X^TX + \lambda I)^{-1}X^TY J(w)=i=1∑N(yi−w0−j=1∑pwjxij)2+λj=1∑pwj2,其中,λ≥0w^=(XTX+λI)−1XTY
调节参数 λ \lambda λ的大小是影响压缩估计的关键, λ \lambda λ越大,惩罚的力度越大,系数则越趋近于0,反之,选择合适的 λ \lambda λ对模型精度来说十分重要。岭回归通过牺牲线性回归的无偏性降低方差,有可能使得模型整体的测试误差较小,提高模型的泛化能力。
在模型的构建中,除了对基础模型的优化之外,最重要的就是参数寻优,模型算法本身的优化如岭回归对线性回归的优化在于在线性回归的损失函数中加入 L 2 L_2 L2正则化项从而牺牲无偏性降低方差。
但是在该过程中,在 L 2 L_2 L2正则化中参数 λ \lambda λ应该选择多少?是0.01、0.1、还是1?到目前为止,我们只能凭经验或者瞎猜,能不能找到一种方法找到最优的参数 λ \lambda λ?
事实上,找到最佳参数的问题本质上属于最优化的内容,因为从一个参数集合中找到最佳的值本身就是最优化的任务之一,我们脑海中浮现出来的算法无非就是:梯度下降法、牛顿法等无约束优化算法或者约束优化算法,但是在具体验证这个想法是否可行之前,我们首先介绍两个最本质概念的区别。
我们很自然的问题就是岭回归中的参数 λ \lambda λ和参数 w w w之间有什么不一样?事实上,参数 w w w是我们通过设定某一个具体的 λ \lambda λ后使用类似于最小二乘法、梯度下降法等方式优化出来的,我们总是设定 λ \lambda λ是多少后才优化出来的参数 w w w。因此,类似于参数 w w w一样,使用最小二乘法或者梯度下降法等最优化算法优化出来的数我们称为参数,类似于 λ \lambda λ一样,我们无法使用最小二乘法或者梯度下降法等最优化算法优化出来的数我们称为超参数。
模型参数是模型内部的配置变量,其值可以根据数据进行估计。
- 进行预测时需要参数。
- 它参数定义了可使用的模型。
- 参数是从数据估计或获悉的。
- 参数通常不由编程者手动设置。
- 参数通常被保存为学习模型的一部分。
- 参数是机器学习算法的关键,它们通常由过去的训练数据中总结得出 。
模型超参数是模型外部的配置,其值无法从数据中估计。 - 超参数通常用于帮助估计模型参数。
- 超参数通常由人工指定。
- 超参数通常可以使用启发式设置。
- 超参数经常被调整为给定的预测建模问题。
参数寻优理论
参数寻优常见的算法有网格搜索,随机搜索和启发式搜索。
-
网格搜索是在所有候选的参数选择中,通过循环遍历,尝试每一种可能性,表现最好的参数就是最终的结果(暴力搜索)。
原理:在一定的区间内,通过循环遍历,尝试每一种可能性,并计算其约束函数和目标函数的值,对满足约束条件的点,逐个比较其目标函数的值,将坏的点抛弃,保留好的点,最后便得到最优解的近似解。
为了评价每次选出的参数的好坏,我们需要选择评价指标,评价指标可以根据自己的需要选择 a c c u r a c y 、 f 1 − s c o r e 、 f − b e t a 、 p e r c i s i o n 、 r e c a l l accuracy、f1-score、f-beta、percision、recall accuracy、f1−score、f−beta、percision、recall等。
同时,为了避免初始数据的划分对结果的影响,我们需要采用交叉验证的方式来减少偶然性,一般情况下网格搜索需要和交叉验证相结合使用。
python的sklearn包中网格搜索函数GridSearchCV:
网格搜索:网格搜索官方文档, 网格搜索结合pipeline
-
随机搜索(random search)是利用随机数去求函数近似的最优解的方法,区别于网格搜索的暴力搜索方式。
原理:在一定的区间内,不断随机地而不是有倾向性产生随机点,并计算其约束函数和目标函数的值,对满足约束条件的点,逐个比较其目标函数的值,将坏的点抛弃,保留好的点,最后便得到最优解的近似解。
这种方法是建立在概率论的基础上,所取随机点越多,则得到最优解的概率也就越大。这种方法存在精度较差的问题,找到近似最优解的效率高于网格搜索。随机搜索一般用于粗选或普查。
python的sklearn包中随机搜索函数RandomizedSearchCV:
随机搜索官方文档 -
启发式搜索
启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search),它是利用问题拥有的启发信息来引导搜索,达到减少搜索范围、降低问题复杂度的目的,这种利用启发信息的搜索过程称为启发式搜索。原理:在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径,提高了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。
启发式搜索有模拟退火算法(SA)、遗传算法(GA)、列表搜索算法(ST)、进化规划(EP)、进化策略(ES)、蚁群算法(ACA)、人工神经网络(ANN)…等。
启发式搜索非常多样化,而且在sklearn包中并没有现成的函数,如果有需要我们可以针对某一种启发式算法的实现过程进行了解,然后用python手动实现。
网格搜索相当于暴力地从参数空间中每个都尝试一遍,然后选择最优的那组参数,这样的方法显然是不够高效的,因为随着参数类别个数的增加,需要尝试的次数呈指数级增长。有没有一种更加高效的调优方式呢?那就是使用随机搜索的方式,这种方式不仅仅高校,而且实验证明,随机搜索法结果比稀疏化网格法稍好(有时候也会极差,需要权衡)。参数的随机搜索中的每个参数都是从可能的参数值的分布中采样的。与网格搜索相比,这有两个主要优点:
- 可以独立于参数数量和可能的值来选择计算成本。
- 添加不影响性能的参数不会降低效率。
pipeline思维
pipeline其实是一种管道思想,即将数据预处理,模型构建等结合在一起,构成一个模型,主要用到的就是 make_pipeline 或者 Pipeline 函数。
pipeline 可以用于下面几处[2]。:
- 模块化 Feature Transform,只需写很少的代码就能将新的 Feature 更新到训练集中。
- 自动化 Grid Search,只要预先设定好使用的 Model 和参数的候选,就能自动搜索并记录最佳的 Model。
- 自动化 Ensemble Generation,每隔一段时间将现有最好的 K 个 Model 拿来做 Ensemble。
下面我们用 Pipeline 对训练集和测试集进行如下操作:
- 先用 StandardScaler 对数据集每一列做标准化处理,(是 transformer)
- 再用 PCA 将原始的 30 维度特征压缩的 2 维度,(是 transformer)
- 最后再用模型 LogisticRegression。(是 Estimator)
- 调用 Pipeline 时,输入由元组构成的列表,每个元组第一个值为变量名,元组第二个元素是 sklearn 中的 transformer 或 Estimator。
注意中间每一步是 transformer,即它们必须包含 fit 和 transform 方法,或者 fit_transform。
最后一步是一个 Estimator,即最后一步模型要有 fit 方法,可以没有 transform 方法。
然后用 Pipeline.fit对训练集进行训练,pipe_lr.fit(X_train, y_train)
再直接用 Pipeline.score 对测试集进行预测并评分 pipe_lr.score(X_test, y_test)
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
pipe_lr = Pipeline([('sc', StandardScaler()),
('pca', PCA(n_components=2)),
('clf', LogisticRegression(random_state=1))
])
pipe_lr.fit(X_train, y_train)
print('Test accuracy: %.3f' % pipe_lr.score(X_test, y_test))
# Test accuracy: 0.947
除了Pipeline函数的调用外,还有make_pipeline函数的使用,看着更为简介一点,可以参考下一节实战的例子。
参数寻优实战
下面通过SVR方法的例子结合pipeline进行调优,
# 我们先来对未调参的SVR进行评价:
from sklearn.svm import SVR # 引入SVR类
from sklearn.pipeline import make_pipeline # 引入管道简化学习流程
from sklearn.preprocessing import StandardScaler # 由于SVR基于距离计算,引入对数据进行标准化的类
from sklearn.model_selection import GridSearchCV # 引入网格搜索调优
from sklearn.model_selection import cross_val_score # 引入K折交叉验证
from sklearn import datasets
boston = datasets.load_boston() # 返回一个类似于字典的类
X = boston.data
y = boston.target
features = boston.feature_names
pipe_SVR = make_pipeline(StandardScaler(),SVR())
score1 = cross_val_score(estimator=pipe_SVR, X = X, y = y, scoring = 'r2', cv = 10) # 10折交叉验证
print("CV accuracy: %.3f +/- %.3f" % ((np.mean(score1)),np.std(score1)))
# 下面我们使用网格搜索来对SVR调参:
from sklearn.pipeline import Pipeline
pipe_svr = Pipeline([("StandardScaler",StandardScaler()), ("svr",SVR())])
param_range = [0.0001,0.001,0.01,0.1,1.0,10.0,100.0,1000.0]
param_grid = [{"svr__C":param_range, "svr__gamma" :param_range, "svr__kernel":["linear", "rbf"]} # 注意__是指两个下划线,一个下划线会报错的
]
gs = GridSearchCV(estimator=pipe_svr, param_grid = param_grid, scoring = 'r2', cv = 10) # 10折交叉验证
gs = gs.fit(X,y)
print("网格搜索最优得分:",gs.best_score_)
print("网格搜索最优参数组合:\n",gs.best_params_)
# 下面我们使用随机搜索来对SVR调参:
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import uniform # 引入均匀分布设置参数
pipe_svr = Pipeline([("StandardScaler",StandardScaler()), ("svr",SVR())])
pipe_svr = make_pipeline()
distributions = dict(svr__C=uniform(loc=1.0, scale=4), # 构建连续参数的分布
svr__kernel=["linear","rbf"], # 离散参数的集合
svr__gamma=uniform(loc=0, scale=4))
rs = RandomizedSearchCV(estimator=pipe_svr, param_distributions = distributions, scoring = 'r2', cv = 10) # 10折交叉验证
rs = rs.fit(X,y)
print("随机搜索最优得分:",rs.best_score_)
print("随机搜索最优参数组合:\n",rs.best_params_)
分类问题建模
分类问题常用的基础模型一般有logistic回归,线性判别分析,朴素贝叶斯,决策树,支持向量机等,下面一一介绍,数据采用Iris数据集:
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
feature = iris.feature_names
data = pd.DataFrame(X,columns=feature)
data['target'] = y
- logistic回归
# 逻辑回归
'''
penalty {‘l1’, ‘l2’, ‘elasticnet’, ‘none’}, default=’l2’正则化方式
dual bool, default=False 是否使用对偶形式,当n_samples> n_features时,默认dual = False。
C float, default=1.0
solver {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}, default=’lbfgs’
l1_ratio float, default=None
'''
from sklearn.linear_model import LogisticRegression
log_iris = LogisticRegression()
log_iris.fit(X,y)
log_iris.score(X,y)
- 线性判别分析
# 线性判别分析
'''
参数:
solver:{'svd','lsqr','eigen'},默认='svd'
solver的使用,可能的值:
'svd':奇异值分解(默认)。不计算协方差矩阵,因此建议将此求解器用于具有大量特征的数据。
'lsqr':最小二乘解,可以与收缩结合使用。
'eigen':特征值分解,可以与收缩结合使用。
'''
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda_iris = LinearDiscriminantAnalysis()
lda_iris.fit(X,y)
lda_iris.score(X,y)
- 朴素贝叶斯
# 朴素贝叶斯
from sklearn.naive_bayes import GaussianNB
NB_iris = GaussianNB()
NB_iris.fit(X, y)
NB_iris.score(X,y)
- 决策树
# 使用决策树算法对iris分类:
'''
criterion:{“gini”, “entropy”}, default=”gini”
max_depth:树的最大深度。
min_samples_split:拆分内部节点所需的最少样本数
min_samples_leaf :在叶节点处需要的最小样本数。
'''
from sklearn.tree import DecisionTreeClassifier
tree_iris = DecisionTreeClassifier(min_samples_leaf=5)
tree_iris.fit(X,y)
tree_iris.score(X,y)
- 支持向量机
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
'''
C:正则化参数。正则化的强度与C成反比。必须严格为正。惩罚是平方的l2惩罚。
kernel:{'linear','poly','rbf','sigmoid','precomputed'},默认='rbf'
degree:多项式和的阶数
gamma:“ rbf”,“ poly”和“ Sigmoid”的内核系数。
shrinking:是否软间隔分类,默认true
'''
svc_iris = make_pipeline(StandardScaler(), SVC(gamma='auto'))
svc_iris.fit(X, y)
svc_iris.score(X,y)
参数调优实战
分别使用网格搜索和随即搜索利用支持向量机和XGBoost方法对模型调优然后分类。
- 网格搜索+SVC
# 使用网格搜索进行超参数调优:
# 方式1:网格搜索GridSearchCV()
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
import time
start_time = time.time()
pipe_svc = make_pipeline(StandardScaler(),SVC(random_state=1))
param_range = [0.0001,0.001,0.01,0.1,1.0,10.0,100.0,1000.0]
param_grid = {'svc__C':param_range,'svc__gamma':param_range,'svc__kernel':['rbf','linear']}
gs = GridSearchCV(estimator=pipe_svc,param_grid=param_grid,scoring='accuracy',cv=10,n_jobs=-1)
gs = gs.fit(X,y)
end_time = time.time()
print("网格搜索经历时间:%.3f S" % float(end_time-start_time))
print(gs.best_score_)
print(gs.best_params_)
- 随机搜索+SVC
# 方式2:随机网格搜索RandomizedSearchCV()
from sklearn.model_selection import RandomizedSearchCV
from sklearn.svm import SVC
import time
start_time = time.time()
pipe_svc = make_pipeline(StandardScaler(),SVC(random_state=1))
param_range = [0.0001,0.001,0.01,0.1,1.0,10.0,100.0,1000.0]
# param_grid = [{'svc__C':param_range,'svc__kernel':['linear']},{'svc__C':param_range,'svc__gamma':param_range,'svc__kernel':['rbf']}]
param_grid = {'svc__C':param_range,'svc__gamma':param_range,'svc__kernel':['rbf','linear']}
gs = RandomizedSearchCV(estimator=pipe_svc, param_distributions=param_grid,scoring='accuracy', cv=10, n_jobs=-1)
gs = gs.fit(X,y)
end_time = time.time()
print("随机网格搜索经历时间:%.3f S" % float(end_time-start_time))
print(gs.best_score_)
print(gs.best_params_)
- 随机搜索+XGBoost
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import GridSearchCV,RandomizedSearchCV
from sklearn.metrics import classification_report
from xgboost.sklearn import XGBClassifier
iris = datasets.load_iris()
parameters = {'n_estimators':range(100,150,10),'max_depth':range(3,5,1)}
xgc=XGBClassifier()
clf = RandomizedSearchCV(xgc, parameters,cv=5)
clf.fit(iris.data, iris.target)
cv_result = pd.DataFrame.from_dict(clf.cv_results_)
best_param=clf.best_params_
best_score=clf.best_score_
y_pred = clf.predict(iris.data)
print(classification_report(y_true=iris.target, y_pred=y_pred))
print(best_score)
混淆矩阵和ROC曲线
下面简单介绍一下混淆矩阵和ROC曲线的绘制,关于其的理论知识以及准确率,召回率等更细致的讲解,可参考本人另一篇文章[3] 模型构建相关的理论知识, 后续也会进一步总结一些理论知识。
当类别为两类时,可以绘制混淆矩阵和ROC曲线。
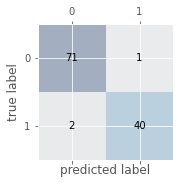
- 混淆矩阵
# 混淆矩阵:
# 加载数据
df = pd.read_csv("http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data",header=None)
'''
乳腺癌数据集:569个恶性和良性肿瘤细胞的样本,M为恶性,B为良性
'''
# 做基本的数据预处理
from sklearn.preprocessing import LabelEncoder
X = df.iloc[:,2:].values
y = df.iloc[:,1].values
le = LabelEncoder() #将M-B等字符串编码成计算机能识别的0-1
y = le.fit_transform(y)
le.transform(['M','B'])
# 数据切分8:2
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,stratify=y,random_state=1)
# stratify是保证分层训练测试集y数据的比例不变
from sklearn.svm import SVC
pipe_svc = make_pipeline(StandardScaler(),SVC(random_state=1))
from sklearn.metrics import confusion_matrix
pipe_svc.fit(X_train,y_train)
y_pred = pipe_svc.predict(X_test)
confmat = confusion_matrix(y_true=y_test,y_pred=y_pred)
fig,ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(confmat, cmap=plt.cm.Blues,alpha=0.3)
for i in range(confmat.shape[0]):
for j in range(confmat.shape[1]): ax.text(x=j,y=i,s=confmat[i,j],va='center',ha='center')
plt.xlabel('predicted label')
plt.ylabel('true label')
plt.show()
- ROC曲线
# 绘制ROC曲线:
from sklearn.metrics import roc_curve,auc
from sklearn.metrics import make_scorer,f1_score
scorer = make_scorer(f1_score,pos_label=0)
gs = GridSearchCV(estimator=pipe_svc,param_grid=param_grid,scoring=scorer,cv=10)
y_pred = gs.fit(X_train,y_train).decision_function(X_test)
#y_pred = gs.predict(X_test)
fpr,tpr,threshold = roc_curve(y_test, y_pred) ###计算真阳率和假阳率
roc_auc = auc(fpr,tpr) ###计算auc的值
plt.figure()
lw = 2
plt.figure(figsize=(7,5))
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假阳率为横坐标,真阳率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([-0.05, 1.0])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic ')
plt.legend(loc="lower right")
plt.show()
总结
本文简单介绍了机器学习的sklearn库中的一些模型的用法,不过都是针对小型数据,也都是从python中自带的数据做的分类和回归,简单介绍了网格搜索和随机搜索,但根据笔者实践,在大数据集上网格搜索极其之慢,非常不合适,通过tensorflow或者pytorch进行处理大数据集一般更为合适,但暂未涉猎在深度学习上的参数寻优方法,后续会做学习和更新文章。