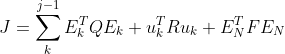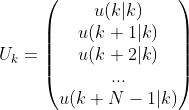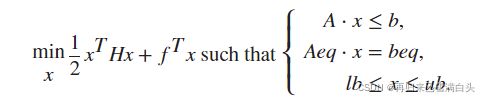Dr_can模型预测控制笔记与代码实现

最近在准备毕业设计，通过看Dr_can的视频来学习一些控制方法，视频链接https://www.bilibili.com/video/BV1cL411n7KV/?spm_id_from=333.788.recommend_more_video.0https://www.bilibili.com/video/BV1cL411n7KV/?spm_id_from=333.788.recommend_more_video.0

由于实际需要，后续应该会更新模型预测控制在非线性领域的应用（自适应MPC,增益调度MPC，非线性MPC）

1.最优控制与代价函数

最优控制（optimal control）指的是在一定的约束情况下达到最优状态的系统表现，其中约束情况通常是实际环境所带来的限制，比如说如果你去控制方向盘的转向，方向盘的转动自身是有一个极限位置的，再比如说，对于一个卫星控制系统，三轴输出的力，力矩都有自己的极大值。

而如何去定义一个最优状态呢？首先引入一个比较直观的例子，汽车的转向变道问题：

正常来说，汽车转向变道应当追求乘客舒适度情况，如下图；

但如果考虑到紧急避障的问题，那么答案就完全不同了，如下图，当汽车前方遭遇到一辆校车急刹车时，为了躲开它，汽车必须尽快地向一侧变道，而不考虑舒适度问题。

因此，最优是需要结合系统面临的实际情况得出的概念，对于不同的应用背景，应当设定不同的指标去衡量优劣，因此我们引入代价函数（Cost Function）的概念：

首先，对于单输入单输出系统（SISO）而言，衡量系统性能优劣可以用误差的积累值（越小，代表误差越小，收敛越快）和输入的积累值（越小，代表控制耗能越少，越节约）来衡量。

由此，我们可以定义代价函数：

函数中的q，r分别表示一个增益系数，如果q大，表示希望误差变得更小，收敛更快；r大，表示更注重输入累积，更注重节能。

接下来，我们把其推广到多输入多输出系统（MIMO），使用状态空间描述为：（这里我们假设前馈矩阵为0）

此时，衡量系统表现优劣就要引入二次型的知识，我们定义：

这里的Q和R矩阵一般是我们设定的对角矩阵，我们来举一个简单的例子：

我们假定期望输入是0，那么：

我们可以通过代价函数J的大小，来衡量系统表现的优劣，当代价函数取最小值时得到的输入，即可被称为是一种“最优输入”。

2.模型预测控制的引入

那么为什么还要引入模型预测控制的概念呢？最优控制中的代价函数需要计算从0时刻到正无穷时刻的积分，这是一种很贪婪的行为，需要消耗大量算力；同时，系统如果是一个时变系统，或者面临扰动的话，前一时刻得到的最优并不一定是下一时刻的最优值。

因而我们引入模型预测控制（Model Predictive Control）的概念，对于一般的离散化系统（因为实际计算机实现的控制系统都是离散的系统，连续系统离散化的方法在此不述）。在k时刻，我们可以测量或估计出系统的当前状态y(k)，再通过计算得到的u(k),u(k+1),u(k+2)...u(k+j)得到系统未来状态的估计值y(k+1),y(k+2)...y(k+j)；我们将预测估计的部分称为预测区间（Predictive Horizon）,将控制估计的部分称为控制区间（Control Horizon），在得到最优输入之后，我们只施加当前时刻的输入u(k)，而放弃接下来得到的输入序列。

总结如下：模型预测控制在k时刻共需三步；

第一步：估计/测量读取系统的当前状态；

第二步：基于u(k),u(k+1),u(k+2)...u(k+j)进行最优化处理；

离散系统的代价函数可以参考

其中EN表示误差的终值，也是衡量优劣的一种标准。

第三步：只取u(k)作为控制输入施加在系统上。

在下一时刻重复以上三步，在下一步进行预测时使用的就是下一步的状态值，我们将这样的方案称为滚动优化控制（Receding Horizon Control）。

可以看到，每一时刻都需要进行一次预测，这对算力提出了巨大的要求，同时我们在此并没考虑约束问题，这个放在之后讨论。

3.最优化建模

实现MPC有许多方法，这里介绍一种方法：二次规划（Quadratic Programming）

我们首先引入一个离散系统：

我们定义：是k时刻预测的输入值，而是k时刻预测的状态值，我们设：

对于期望输入为0，输出向量等于状态向量的离散系统：

我们可以得到代价函数：

其中，我们需要求解的是系统的输入u(k)，这就需要我们把状态项x(k)给消除掉，处理这个事情需要利用系统的状态方程，首先有

我们可以通过传感器或者状态估计得到系统当前的状态值，这相当于系统的一个初值，由初值和状态方程可以得到其他项为：

我们把它简单整理一下，有：

我们再令：

我们就得到了最简单的形式：

即：

上式还可根据之前推导的公式继续化简，

其中，与互为转置，但他们彼此又都是常数，所以他们彼此相等，因此有：

再令

有：

由此我们就得到了模型预测控制代价函数的简单形式。

4.一个详细建模实例与完整代码

下面直接上得到最优输入U_k的代码

function U_k=MPC(A,B,N,x_k,Q,R,F)
%%%%%%%%%%%%%%%%%%%%%%%%
n = size(A,1); %% A矩阵是n * n矩阵，得到A矩阵的维数
p = size(B,2); %% B矩阵是n * p矩阵，得到B矩阵的维数
M = [eye(n);zeros(N*n,n)]; %% 初始化M矩阵,第一个分块矩阵置单位阵，其余矩阵置零
C = zeros((N+1)*n,N*p); %% 初始化C矩阵，置零
%接下来计算完整的M矩阵与C矩阵
tmp = eye(n); %定义一个n阶单位阵，工具人
for i = 1:N
    rows = i*n + (1:n);%行数，因为是分块矩阵所以从1至n;
    C(rows, :) = [tmp*B, C(rows-n, 1:end-p)];%用遍历的方法将C矩阵填满;
    tmp = A*tmp;%每次都左乘一次A矩阵;
    M(rows,:) = tmp;%写满M矩阵;
end
%定义Q_bar和R_bar
S_q = size(Q,1);%得到Q矩阵维度
S_r = size(R,1);%得到R矩阵维度
Q_bar = zeros((N+1)*S_q,(N+1)*S_q);%定义Q_bar矩阵维度
R_bar = zeros(N*S_r,N*S_r);%定义R_bar矩阵维度
for i = 0:N-1
    Q_bar(i*S_q+1:(i+1)*S_q,i*S_q+1:(i+1)*S_q) = Q;%把对角线上写满Q
end
Q_bar(N*S_q+1:(N+1)*S_q, N*S_q+1:(N+1)*S_q) = F;%最后一块写上F
for i = 0:N-1
        R_bar(i*S_r+1:(i+1)*S_r, i*S_r+1:(i+1)*S_r) = R;%对角线上写满R
end
G = M'*Q_bar*M;%定义M矩阵，事实上在代价函数中，这和输入无关，并没有被用到
E = M'*Q_bar*C;%定义E矩阵
H = C'*Q_bar*C + R_bar;%定义H矩阵
%最优化，得到最优输入值
f = x_k'*E;%由于quadprog函数的定义，需要把其写成矩阵相乘形式
%基于实际情况，给输入加约束
D = eye(3);b = [10;10;10];Aep=[];Bep=[];c=[1;1;1];d=[-1;-1;-1];
U_k = quadprog(H,f,D,b,Aep,Bep,d,c);%求解最优的U_k值

代码中有几个值得注意的点：

1.矩阵的维度，这里面涉及矩阵很多，很容易把维度搞晕，建议自己手推一次，效果很好。

2.这段填满C矩阵的过程稍微有点难懂，是对照着C矩阵的结构以及里面的规律写出来的。

for i = 1:N
    rows = i*n + (1:n);%行数，因为是分块矩阵所以从1至n;
    C(rows, :) = [tmp*B, C(rows-n, 1:end-p)];%用遍历的方法将C矩阵填满;
    tmp = A*tmp;%每次都左乘一次A矩阵;
    M(rows,:) = tmp;%写满M矩阵;
end

 3.得到最优控制输入的函数quadprog，根据Matlab自带文档描述，它是求解下列问题最小值的函数，可以添加约束，由一个二次型描述与一个线性描述组成，为了使控制器的表现更贴近实际，我给输出加了正负1的限制。

 接下来，我来做一个完整的仿真过程，并比对不同Q,F,R对系统的影响，假设有离散系统为：

我们设A矩阵，B矩阵分别为：

输出的期望值为零向量，设置不同的Q,R,F矩阵，进行仿真；

在第一种情况，我们令：

在第二种情况，我们令：

显然，在第一种情况我们更在意误差的收敛速度，而在第二种情况我们更在意能量消耗的多少，下面是仿真结果：

 可以明显得看到，情况一收敛速度更快，耗能更多，而情况二收敛速度更慢，耗能更少，符合之前的预测。

下面是完整仿真代码：

%h为一个更新周期，即积分步长，采样时间为n
%假定输入为零，输出即为状态值
clear
clc
format long 
%--------------------------初始参数---------------------------------%
h=0.1;                      %仿真步长              
n=300;                      %仿真时间   
NN=n/h;
A = [1,0.1;0,1];            %系统矩阵
B = [0;0.5];                %输入矩阵
Q = [2,0;0,2];              %Q矩阵，对误差积累的重视程度
R = 0.1;                    %R系数，表示对节省输入的重视程度
N = 3;                      %预测区间
F = [2,0;0,2];              %F矩阵，对终端误差的重视程度
x_0 = [100;100];            %初始位置
X1 = zeros(2,NN+1);          
t = zeros(1,NN+1);
U1 = zeros(1,NN+1);         %初始化
Eg1 = zeros(1,NN+1);
X1(:,1) = x_0;              %赋初值
%--------------------------仿真1开始---------------------------------%
for j = 1:NN
    U_all = MPC(A,B,N,X1(:,j),Q,R,F);
    X1(:,j+1) = A*X1(:,j) + B*U_all(1);       %这里只取预测估计的第一项
    U1(j) = U_all(1);
    t(j+1)=t(j)+h;
    Eg1(j+1) = Eg1(j)+U_all(1)^2;
end
%%为了比较不同参数的影响，选择另一组Q,R,F
Q = [0.1,0;0,0.1];          %Q矩阵，对误差积累的重视程度
R = 10;                     %R系数，表示对节省输入的重视程度
F = [0.1,0;0,0.1];          %F矩阵，对终端误差的重视程度
X2 = zeros(2,NN+1); 
U2 = zeros(1,NN+1);         %初始化
Eg2 = zeros(1,NN+1);
X2(:,1) = x_0;              %赋初值
%--------------------------仿真2开始---------------------------------%
for j = 1:NN
    U_all = MPC(A,B,N,X2(:,j),Q,R,F);
    X2(:,j+1) = A*X2(:,j) + B*U_all(1);     %这里只取预测估计的第一项
    U2(j) = U_all(1);
    t(j+1)=t(j)+h;
    Eg2(j+1) = Eg2(j)+U_all(1)^2;
end
figure(1)
subplot(2,1,1),plot(t,X1(1,:),'-','linewidth',3),title('状态向量'),ylabel('x_1');hold on;
plot(t,X2(1,:),'-','linewidth',2),title('状态向量'),ylabel('x_1');grid on;
legend('case1','case2');
subplot(2,1,2),plot(t,X1(2,:),'-','linewidth',3),xlabel('t/s'),ylabel('x_2');hold on
plot(t,X2(2,:),'-','linewidth',2),title('状态向量'),ylabel('x_2');grid on;
legend('case1','case2');
figure(2)
plot(t,U1,'linewidth',2),title('实际输入'),xlabel('t/s'),ylabel('u');hold on;
plot(t,U2,'linewidth',2),title('实际输入'),xlabel('t/s'),ylabel('u');grid on;
legend('case1','case2');
figure(3)
plot(t,Eg1,'linewidth',2),title('消耗能量'),xlabel('t/s'),ylabel('J');hold on;
plot(t,Eg2,'linewidth',2),title('消耗能量'),xlabel('t/s'),ylabel('J');grid on;
legend('case1','case2');