自然语言处理-中文分词相关算法(MM、RMM、BMM、HMM)
文章目录
- 一、前言
- 二、分词算法
-
- 2.1 规则分词
-
- 2.1.1 正向最大匹配法
- 2.1.2 逆向最大匹配法
- 2.1.3 双向最大匹配法
- 2.2 统计分词
-
- 2.2.1 语言模型
- 2.2.2 HMM模型
- 2.3 混合分词
- 三、中文分词工具
- 四、参考链接
- 五、源码获取
一、前言
关于中文分词的介绍,之前已经详细的介绍过了,此篇博文的重点是介绍一些具体的分词方法。
二、分词算法
自中文自动分词被提出以来,历经将近30 年的探索,提出了很多方法,可主要归纳为"规则分词"、统计分词"和"混合分词(规则+统计)"这三个主要流派。规则分词是最早兴起的方法,主要是通过人工设立词库,按照一定方式进行匹配切分,其实现简单高效,但对新词很难进行处理。随后统计机器学习技术的兴起,应用于分词任务上后,就有了统计分词,能够较好应对新词发现等特殊场景。然而实践中,单纯的统计分词也有缺陷,那就是太过于依赖语料的质量,因此实践中多是采用这两种方法的结合,即混合分词。此博文主要介绍一些关于分词的一些算法。
2.1 规则分词
基于规则的分词是一种机械分词方法,主要是通过维护词典,在切分语句时,将语句的每个字符串与词表中的词进行逐一匹配,找到则切分,否则不切分。
按照匹配切分的方式,主要有正向最大匹配法,逆向最大匹配法以及双向最大匹配法三种方法。
2.1.1 正向最大匹配法
正向最大匹配( Maximum Match Method , MM 法)的基本思想:假定分词词典中的最长词有 i i i个汉字字符,则用被处理文档的当前字串中的前 i i i个字作为匹配字段,查找字典。若字典中存在这个的一个 i i i字词,则匹配成功,匹配字段被作为一个词切分出来。如果字典中找不到这样的一个 i i i字词,则匹配失败,将匹配字段中的最后一个字去掉,对剩下的字串重新进行匹配处理。如此进行下去,直到匹配成功,即切分处一个词或剩余字串的长度为零为止。这样就完成了一轮匹配,然后去下一个 i i i字字串进行匹配处理,直到文档被扫描完为止。
其算法描述如下:
1、从左向右取待切分汉语句的m个字符作为匹配字段, m为机器词典中最长词条的字符数。
2、查找机器词典并进行匹配。若匹配成功,则将这个匹配字段作为一个词切分出来。若匹配不成功,则将这个匹配字段的最后一个字去掉,剩下的字符串作为新的匹配字段,进行再次匹配, 重复以上过程,直到切分出所有词为止。
具体算法描述如下所示:
正向即从前往后取词,从7->1,每次减一个字,直到词典命中或剩下1个单字。
第一轮扫描
第1次:“我们在野生动物”,扫描7字词典,无
第2次:“我们在野生动”,扫描6字词典,无
。。。。
第6次:“我们”,扫描2字词典,有
扫描中止,输出第1个词为“我们”,去除第1个词后开始第2轮扫描,即:
第2轮扫描:
第1次:“在野生动物园玩”,扫描7字词典,无
第2次:“在野生动物园”,扫描6字词典,无
。。。。
第6次:“在野”,扫描2字词典,有
扫描中止,输出第2个词为“在野”,去除第2个词后开始第3轮扫描,即:
第3轮扫描:
第1次:“生动物园玩”,扫描5字词典,无
第2次:“生动物园”,扫描4字词典,无
第3次:“生动物”,扫描3字词典,无
第4次:“生动”,扫描2字词典,有
扫描中止,输出第3个词为“生动”,第4轮扫描,即:
第4轮扫描:
第1次:“物园玩”,扫描3字词典,无
第2次:“物园”,扫描2字词典,无
第3次:“物”,扫描1字词典,无
扫描中止,输出第4个词为“物”,非字典词数加1,开始第5轮扫描,即:
第5轮扫描:
第1次:“园玩”,扫描2字词典,无
第2次:“园”,扫描1字词典,有
扫描中止,输出第5个词为“园”,单字字典词数加1,开始第6轮扫描,即:
第6轮扫描:
第1次:“玩”,扫描1字字典词,有
扫描中止,输出第6个词为“玩”,单字字典词数加1,整体扫描结束。
正向最大匹配法,最终切分结果为:“我们/在野/生动/物/园/玩”,其中,单字字典词为2,非词典词为1。
程序实现(Python)
# """
# author:jjk
# datetime:2019/5/3
# coding:utf-8
# project name:Pycharm_workstation
# Program function: 正向最大匹配( Maximum Match Method , MM 法)分词
# """
"""
S1、导入分词词典input.txt,存储为字典形式dic、导入停用词词典stop_words.utf8 ,存储为字典形式stoplis、需要分词的文本文件 fenci.txt,存储为字符串chars
S2、遍历分词词典,找出最长的词,其长度为此算法中的最大分词长度max_chars
S3、创建空列表words存储分词结果
S4、初始化字符串chars的分词起点n=0
S5、判断分词点n是否在字符串chars内,即n < len(chars) 如果成立,则进入下一步骤,否则进入S9
S6、根据分词长度i(初始值为max_chars)截取相应的需分词文本chars的字符串s
S7、判断s是否存在于分词词典中,若存在,则分两种情况讨论,一是s是停用词,那么直接删除,分词起点n后移i位,转到步骤5;
二是s不是停用词,那么直接添加到分词结果words中,分词起点n后移i位,
转到步骤5;若不存在,则分两种情况讨论,一是s是停用词,那么直接删除,分词起点后移i位,
转到步骤5;二是s不是停用词,分词长度i>1时,分词长度i减少1,
转到步骤6 ,若是此时s是单字,则转入步骤8;
S8、将s添加到分词结果words中,分词起点n后移1位,转到步骤5
S9、将需分词文本chars的分词结果words输出到文本文件result.txt中
"""
import codecs
#分词字典
f1 = codecs.open('input.txt', 'r', encoding='utf8')
dic = {}
while 1:
line = f1.readline()
if len(line) == 0:
break
term = line.strip() #去除字典两侧的换行符,避免最大分词长度出错
dic[term] = 1
f1.close()
#获得需要分词的文本
f2 = codecs.open('fenci.txt', 'r', encoding='utf8')
chars = f2.read().strip()
f2.close()
#停用词典,存储为字典形式
f3 = codecs.open('stop_words.utf8', 'r', encoding='utf8')
stoplist = {}
while 1:
line = f3.readline()
if len(line) == 0:
break
term = line.strip()
stoplist[term] = 1
f3.close()
"""
正向匹配最大分词算法
遍历分词词典,获得最大分词长度
"""
max_chars = 0
for key in dic:
if len(key) > max_chars:
max_chars = len(key)
#定义一个空列表来存储分词结果
words = []
n = 0
while n < len(chars):
matched = 0
#range([start,] stop[, step]),根据start与stop指定的范围以及step设定的步长 step=-1表示去掉最后一位
for i in range(max_chars, 0, -1): #i等于max_chars到1
s = chars[n : n + i] #截取文本字符串n到n+1位
#判断所截取字符串是否在分词词典和停用词词典内
if s in dic:
if s in stoplist: #判断是否为停用词
words.append(s)
matched = 1
n = n + i
break
else:
words.append(s)
matched = 1
n = n + i
break
if s in stoplist:
words.append(s)
matched = 1
n = n + i
break
if not matched: #等于 if matched == 0
words.append(chars[n])
n = n + 1
#分词结果写入文件
f3 = open('MMresult.txt','w', encoding='utf8') # 输出结果写入到MMresult.txt中
f3.write('/'.join('%s' %id for id in words))
print('/'.join('%s' %id for id in words)) # 打印到控制台
f3.close() # 关闭文件指针
2.1.2 逆向最大匹配法
逆向最大匹配( Reverse Maximum Match Method , RMM 法)的基本原理与MM 法相同,不同的是分词切分的方向与MM 法相反。逆向最大匹配法从被处理文档的末端开始匹配扫描,每次取最末端的i个字符( i 为词典中最长词数)作为匹配字段,若匹配失败,则去掉匹配字段最前面的一个字,继续匹配。相应地,它使用的分词词典是逆序词典,其中的每个词条都将按逆序方式存放。在实际处理时,先将文档进行倒排处理,生成逆序文挡。然后,根据逆序词典,对逆序文档用正向最大匹配法处理即可。
由于汉语中偏正结构较多, 若从后向前匹配,可以适当提高精确度。所以,逆向最大匹配法比正向最大匹配法的误差要小。
具体算法描述如下所示:
逆向即从后往前取词,其他逻辑和正向相同。即:
第1轮扫描:“在野生动物园玩”
第1次:“在野生动物园玩”,扫描7字词典,无
第2次:“野生动物园玩”,扫描6字词典,无
。。。。
第7次:“玩”,扫描1字词典,有
扫描中止,输出“玩”,单字字典词加1,开始第2轮扫描
第2轮扫描:“们在野生动物园”
第1次:“们在野生动物园”,扫描7字词典,无
第2次:“在野生动物园”,扫描6字词典,无
第3次:“野生动物园”,扫描5字词典,有
扫描中止,输出“野生动物园”,开始第3轮扫描
第3轮扫描:“我们在”
第1次:“我们在”,扫描3字词典,无
第2次:“们在”,扫描2字词典,无
第3次:“在”,扫描1字词典,有
扫描中止,输出“在”,单字字典词加1,开始第4轮扫描
第4轮扫描:“我们”
第1次:“我们”,扫描2字词典,有
扫描中止,输出“我们”,整体扫描结束。
逆向最大匹配法,最终切分结果为:“我们/在/野生动物园/玩”,其中,单字字典词为2,非词典词为0。
程序实现
# """
# author:jjk
# datetime:2019/5/3
# coding:utf-8
# project name:Pycharm_workstation
# Program function: 逆向最大匹配(Reverse Maximum Match Method , RMM 法)分词
# """
class IMM(object):
def __init__(self,dic_path):
self.dictionary=set()
self.maximum = 0
# 读取字典
with open(dic_path,'r',encoding='utf8') as f:
for line in f:
line = line.strip()
if line:
self.dictionary.add(line)
self.maximum = len(self.dictionary)
def cut(self,text):
# 用于存放切分出来的词
result = []
index = len(text)
# 记录没有在词典中的词,可以用于发现新词
no_word = ''
while index>0:
word = None
# 从前往后匹配,以此实现最大匹配
for first in range(index):
if text[first:index] in self.dictionary:
word = text[first:index]
# 如果之前存放字典里面没有出现过的词
if no_word != '':
result.append(no_word[::-1])
no_word = ''
result.append(text[first:index])
index = first
break
if word == None:
index = index - 1
no_word += text[index]
return result[::-1]
def main():
text = '南京市长江大桥'
tokenizer = IMM('imm_dic.utf8') # 调用类函数
print(tokenizer.cut(text)) # 输出
if __name__ == '__main__':
main()
2.1.3 双向最大匹配法
双向最大匹配法( Bi-directction Matching method ) 是将正向最大匹配法得到的分词结果和逆向最大匹配法得到的结果进行比较,然后按照最大匹配原则,选取词数切分最少的作为结果。据SunM.S. 和Benjamin K.T. ( 1995 )的研究表明,中文中90.0% 左右的句子,正向最大匹配法和逆向最大匹配法完全重合且正确,只有大概9 .0% 的句子两种切分方法得到的结果不一样,但其中必有一个是正确的(歧义检测成功) ,只有不到1.0%的句子,使用正向最大匹配法和逆向最大匹配法的切分虽重合却是错的,或者正向最大匹配法和逆向最大匹配法切分不同但两个都不对(歧义检测失败) 。这正是双向最大匹配法在实用中文信息处理系统中得以广泛使用的原因。
具体算法描述如下所示:
正向最大匹配法和逆向最大匹配法,都有其局限性,因此有人又提出了双向最大匹配法。即,两种算法都切一遍,然后根据大颗粒度词越多越好,非词典词和单字词越少越好的原则,选取其中一种分词结果输出。如:“我们在野生动物园玩”
正向最大匹配法,最终切分结果为:“我们/在野/生动/物/园/玩”,其中,两字词3个,单字字典词为2,非词典词为1。
逆向最大匹配法,最终切分结果为:“我们/在/野生动物园/玩”,其中,五字词1个,两字词1个,单字字典词为2,非词典词为0。
非字典词:正向(1)>逆向(0)(越少越好)
单字字典词:正向(2)=逆向(2)(越少越好)
总词数:正向(6)>逆向(4)(越少越好)
因此最终输出为逆向结果。
源码实现
package test;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashSet;
import java.util.Set;
import java.util.Vector;
public class FBSegment {
private static Set<String> seg_dict;
//加载词典
public static void Init(){
seg_dict = new HashSet<String>();
String dicpath = "F:\\IDEA\\IDEA_workstation\\src\\test\\input.txt";
String line = null;
try{
BufferedReader br = new BufferedReader( new InputStreamReader(new FileInputStream(dicpath)));
while((line = br.readLine()) != null){
line = line.trim();
if(line.isEmpty())
continue;
seg_dict.add(line);
}
br.close();
}catch(IOException e){
e.printStackTrace();
}
}
/**
* 前向算法分词
* @param seg_dict 分词词典
* @param phrase 待分词句子
* @return 前向分词结果
*/
private static Vector<String> FMM2( String phrase){
int maxlen = 16;
Vector<String> fmm_list = new Vector<String>();
int len_phrase = phrase.length();
int i=0,j=0;
while(i < len_phrase){
int end = i+maxlen;
if(end >= len_phrase)
end = len_phrase;
String phrase_sub = phrase.substring(i, end);
for(j = phrase_sub.length(); j >=0; j--){
if(j == 1)
break;
String key = phrase_sub.substring(0, j);
if(seg_dict.contains(key)){
fmm_list.add(key);
i +=key.length() -1;
break;
}
}
if(j == 1)
fmm_list.add(""+phrase_sub.charAt(0));
i+=1;
}
return fmm_list;
}
/**
* 后向算法分词
* @param seg_dict 分词词典
* @param phrase 待分词句子
* @return 后向分词结果
*/
private static Vector<String> BMM2( String phrase){
int maxlen = 16;
Vector<String> bmm_list = new Vector<String>();
int len_phrase = phrase.length();
int i=len_phrase,j=0;
while(i > 0){
int start = i - maxlen;
if(start < 0)
start = 0;
String phrase_sub = phrase.substring(start, i);
for(j = 0; j < phrase_sub.length(); j++){
if(j == phrase_sub.length()-1)
break;
String key = phrase_sub.substring(j);
if(seg_dict.contains(key)){
bmm_list.insertElementAt(key, 0);
i -=key.length() -1;
break;
}
}
if(j == phrase_sub.length() -1)
bmm_list.insertElementAt(""+phrase_sub.charAt(j), 0);
i -= 1;
}
return bmm_list;
}
/**
* 该方法结合正向匹配和逆向匹配的结果,得到分词的最终结果
* @param FMM2 正向匹配的分词结果
* @param BMM2 逆向匹配的分词结果
* @param return 分词的最终结果
*/
public static Vector<String> segment( String phrase){
Vector<String> fmm_list = FMM2(phrase);
Vector<String> bmm_list = BMM2(phrase);
//如果正反向分词结果词数不同,则取分词数量较少的那个
if(fmm_list.size() != bmm_list.size()){
if(fmm_list.size() > bmm_list.size())
return bmm_list;
else return fmm_list;
}
//如果分词结果词数相同
else{
//如果正反向的分词结果相同,就说明没有歧义,可返回任意一个
int i ,FSingle = 0, BSingle = 0;
boolean isSame = true;
for(i = 0; i < fmm_list.size(); i++){
if(!fmm_list.get(i).equals(bmm_list.get(i)))
isSame = false;
if(fmm_list.get(i).length() ==1)
FSingle +=1;
if(bmm_list.get(i).length() ==1)
BSingle +=1;
}
if(isSame)
return fmm_list;
else{
//分词结果不同,返回其中单字较少的那个
if(BSingle > FSingle)
return fmm_list;
else return bmm_list;
}
}
}
public static void main(String [] args){
String test = "南京市长江大桥";
FBSegment.Init();
System.out.println(FBSegment.segment(test));
}
}
2.2 统计分词
随着大规模语料库的建立,统计机器学习方法的研究和发展,基于统计的中文分词算法渐渐成为主流。
其主要思想是把每个词看做是由词的最小单位的各个字组成的,如果相连的字在不同的文本中出现的次数越多,就证明这相连的字很可能就是一个词。因此我们就可以利用字与字相邻出现的频率来反应成词的可靠度,统计语料中相邻共现的各个字的组合的频度,当组合频度高于某一个临界值时,我们便可认为此字组可能会构成一个词语。
1 ) 建立统计语言模型。
2 ) 对句子进行单词划分,然后对划分结果进行概率计算,获得概率最大的分词方式。这里就用到了统计学习算法,如隐含马尔可夫(HMM) 、条件随机场(CRF) 等。
2.2.1 语言模型
语言模型在信息检索、机器翻译、语音识别中承担着重要的任务。用概率论的专业术语描述语言模型就是:长度为 m m m的字符串确定其概率分布:
P ( w 1 , w 2 , . . . , w m ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) . . . P ( w i ∣ w 1 , w 2 , . . . w i − 1 ) , . . . w i ) . . . P ( w m ∣ w 1 , w 2 , . . . w m − 1 ) ( 1 ) P(w_1{},w_2{},...,w_m{})=P(w_1{})P(w_2{}|w_1{})P(w_3{}|w_1,w_2{})...P(w_i{}|w_1{},w_2{},...w_{_i-1}),...w_i{})...P(w_m{}|w_1{},w_2{},...w_{_m-1}) (1) P(w1,w2,...,wm)=P(w1)P(w2∣w1)P(w3∣w1,w2)...P(wi∣w1,w2,...wi−1),...wi)...P(wm∣w1,w2,...wm−1)(1)
由上式可得,当文本过长时,公式右部从第三项起的每一项计算难度都很大。从而有人提出了 n n n元模型( n − g r a m m o d e l n-gram model n−grammodel)降低该计算难度。
所谓 n n n元模型就是在估算条件概率时,忽略距离大于等于 n n n的上下文词的影响,因此 . P ( w i ∣ w 1 , w 2 , . . . w i − 1 ) .P(w_i{}|w_1{},w_2{},...w_{_i-1}) .P(wi∣w1,w2,...wi−1)的计算可简化为: P ( w i ∣ w 1 , w 2 , . . . w i − 1 ) ≈ P ( w i ∣ w i − ( n − 1 ) , . . . , w i − 1 ) ( 2 ) P(w_i{}|w_1{},w_2{},...w_{_i-1})≈P(w_i|w_{i-(n-1),}...,w_{i-1})(2) P(wi∣w1,w2,...wi−1)≈P(wi∣wi−(n−1),...,wi−1)(2),
当 n = 1 n=1 n=1时,称为一元模型,此时整个句子的概率可表示为: P ( w 1 , w 2 , . . . , w m ) = P ( w i ) P ( w 1 ) P ( w 2 ) . . . P ( w m ) P(w_1{},w_2{},...,w_m{})=P(w_i)P(w_1)P(w_2)...P(w_m) P(w1,w2,...,wm)=P(wi)P(w1)P(w2)...P(wm),在一元语言模型中,整个句子的概率等于各个词语概率的乘积。也就是说各个词之间之间都是相互独立的,这无疑是完全损失了句子中词序信息。所以一元模型的效果固然不好。
当 n = 2 n=2 n=2时称为二元模型,将公式2变为: P ( w i ∣ w 1 , w 2 , . . . w i − 1 ) = P ( w i ∣ w i − 1 ) P(w_i{}|w_1{},w_2{},...w_{_i-1})=P(w_i|w_{i-1}) P(wi∣w1,w2,...wi−1)=P(wi∣wi−1)。
当 n = 3 n=3 n=3时称为三元模型,将公式2变为: P ( w i ∣ w 1 , w 2 , . . . w i − 1 ) = P ( w i ∣ w i − 2 , w i − 1 ) P(w_i{}|w_1{},w_2{},...w_{_i-1})=P(w_i|w_{i-2},w_{i-1}) P(wi∣w1,w2,...wi−1)=P(wi∣wi−2,wi−1)。
显然当 n ≥ 2 n≥2 n≥2时,该模型是可以保留一定的词序信息的,而且 n n n越大,保留的词性信息越丰富,但要考虑计算成本奥。
一般使用频率计数的比例来计算 n n n元条件概率,如: P ( w i ∣ w 1 , w 2 , . . . w i − 1 ) = c o u n t ( w i − ( n − 1 ) , . . . , w i − 1 , w i ) c o u n t ( w i − ( n − 1 ) , . . . w i − 1 ) ( 3 ) P(w_i{}|w_1{},w_2{},...w_{_i-1})=\frac{count(w_{i-(n-1)},...,w_{i-1},w_i)}{count(w_{i-(n-1)},...w_{i-1})}(3) P(wi∣w1,w2,...wi−1)=count(wi−(n−1),...wi−1)count(wi−(n−1),...,wi−1,wi)(3) 公中 c o u n t ( w i − ( n − 1 ) , . . . w i − 1 ) {count(w_{i-(n-1)},...w_{i-1})} count(wi−(n−1),...wi−1)表示词语 w i − ( n − 1 ) , . . . w i − 1 w_{i-(n-1)},...w_{i-1} wi−(n−1),...wi−1在语料库中出现的总次数。
由此可见,当 n n n越大时,模型包含的词序信息越丰富,同时计算量随之增大。与此同时,长度越长的文本序列出现的次数也会越少,如公式3估计n元条件概率时,就会出现分子分母为零的情况。因此,一般在n元模型中需要配合相应的平滑算法解决该方法,如拉普拉斯平滑算法等。
2.2.2 HMM模型
隐含马尔可夫模型(HMM) 是将分词作为字在字串中的序列标注任务来实现的。其基本思路是: 每个字在构造一个特定的词语时都占据着一个确定的构词位置(即词位),现规定每个字最多只有四个构词位置: 即B (词首)、M( 词中)、E (词尾)和s (单独成词) ,那么下面句子1 )的分词结果就可以直接表示成如2) 所示的逐字标注形式:
1 ) 中文/ 分词/是1. 文本处理/不可或缺/的/ 一步!
2 ) 中/B 文/E 分/B 词/E 是/S 文/B 本/B 处/M 理/E 不/B 可/M 或/M 缺/E 的/S一/B 步/E ! /S
用数学抽象表示如下:用 λ = λ 1 λ 2 λ 3 . . . λ n \lambda=\lambda_1\lambda_2\lambda_3...\lambda_n λ=λ1λ2λ3...λn代表输入的句子, n n n为句子长度, λ i \lambda_i λi表示字, o = o 1 o 2 . . . o n o=o_1o_2...o_n o=o1o2...on代表输出的标签,那么理想的输出即为:
m a x = m a x P ( o 1 o 2 . . . o n ∣ λ 1 λ 2 λ 3 . . . λ n ) ( 1 ) max=maxP(o_1o_2...o_n|\lambda_1\lambda_2\lambda_3...\lambda_n) (1) max=maxP(o1o2...on∣λ1λ2λ3...λn)(1)
在分词任务上, o o o即为B,M,E,S这四中标记, λ \lambda λ为诸如“中” “文”等句子中的每个字(包括标点等非中文字符)。
需要注意的是, P ( o ∣ λ ) P(o|\lambda) P(o∣λ)均是关于2n 个变量的条件概率,且n 不固定。因此,几乎无法对 P ( o ∣ λ ) P(o|\lambda) P(o∣λ)进行精确计算。这里引人观测独立性假设,即每个字的输出仅仅与当前字有关,于是就能得到下式:
P ( o 1 o 2 . . . o n ∣ λ 1 λ 2 λ 3 . . . λ n ) = P ( o 1 ∣ λ 1 ) P ( o 2 ∣ λ 2 ) . . . P ( o n ∣ λ n ) ( 2 ) P(o_1o_2...o_n|\lambda_1\lambda_2\lambda_3...\lambda_n) =P(o_1|\lambda_1)P(o_2|\lambda_2)...P(o_n|\lambda_n) (2) P(o1o2...on∣λ1λ2λ3...λn)=P(o1∣λ1)P(o2∣λ2)...P(on∣λn)(2)
事实上, P ( o k ∣ λ k ) P(o_k|\lambda_k) P(ok∣λk)的计算要容易得多。通过观测独立性假设,目标问题得到极大简化。然而该方法完全没有考虑上下文,且会出现不合理的情况。比如按照之前设定的B 、M、E 和S 标记,正常来说B后面只能是M或者E ,然而基于观测独立性假设,我们很可能得到诸如BBB 、BEM 等的输出,显然是不合理的。
HMM 就是用来解决该问题的一种方法。在上面的公式中,我们一直期望求解的是 P ( o ∣ λ ) P(o|λ) P(o∣λ),通过贝叶斯公式能够得到:
P ( o ∣ λ ) = P ( o ∣ λ ) P ( λ ) = P ( λ ∣ o ) P ( o ) P ( λ ) ( 3 ) P(o|λ)=\frac{P(o|λ)}{P(λ)}=\frac{P(λ|o)P(o)}{P(λ)} (3) P(o∣λ)=P(λ)P(o∣λ)=P(λ)P(λ∣o)P(o)(3)
λ λ λ为给定的输入,因此 P ( λ ) P(λ) P(λ)计算为常数,可以忽略,因此最大化 P ( o ∣ λ ) P(o|λ) P(o∣λ)等价于最大化 P ( λ ∣ o ) P ( o ) P(λ|o)P(o) P(λ∣o)P(o)。
针对 P ( λ ∣ o ) P ( o ) P(λ|o)P(o) P(λ∣o)P(o)作马尔科夫假设,得到:
P ( λ ∣ o ) = P ( λ 1 ∣ o 1 ) P ( λ 2 ∣ O 2 ) . . . P ( λ n ∣ o n ) ( 4 ) P(λ|o)=P(λ_1|o_1)P(λ_2|O_2)...P(λ_n|o_n) (4) P(λ∣o)=P(λ1∣o1)P(λ2∣O2)...P(λn∣on)(4)
同时,对 P ( o ) P(o) P(o)有:
P ( o ) = P ( o 1 ) P ( o 2 ∣ o 1 ) P ( o 3 ∣ o 1 , o 2 ) . . . P ( o n ∣ o 1 , o 2 , . . . , o n − 1 ) ( 5 ) P(o) =P(o_1)P(o_2|o_1)P(o_3|o_1,o_2)...P(o_n|o_1,o_2,...,o_{n-1}) (5) P(o)=P(o1)P(o2∣o1)P(o3∣o1,o2)...P(on∣o1,o2,...,on−1)(5)
这里HMM做了另外一个假设——齐次马尔科夫假设,每个输出仅仅与上一个输出有关,那么:
P ( o ) = P ( o 1 ) P ( o 2 ∣ o 1 ) P ( o 3 ∣ o 1 , o 2 ) . . . P ( o n ∣ o 1 , o 2 , . . . , o n − 1 ) ( 6 ) P(o)=P(o_1)P(o_2|o_1)P(o_3|o_1,o_2)...P(o_n|o_1,o_2,...,o_{n-1}) (6) P(o)=P(o1)P(o2∣o1)P(o3∣o1,o2)...P(on∣o1,o2,...,on−1)(6)
于是:
P ( λ ∣ o ) P ( o ) — P ( λ 1 ∣ o 1 ) P ( o 2 ∣ o 1 ) P ( λ 2 ∣ o 2 ) P ( o 3 ∣ o 2 ) . . . P ( o n − 1 P ( λ n ∣ o n ) ) ( 7 ) P(λ|o)P(o)—P(λ_1|o_1)P(o_2|o_1)P(λ_2|o_2)P(o_3|o_2)...P(o_{n-1}P(λ_n|o_n)) (7) P(λ∣o)P(o)—P(λ1∣o1)P(o2∣o1)P(λ2∣o2)P(o3∣o2)...P(on−1P(λn∣on))(7)
在HMM中,将 P ( λ k ∣ o k ) P(λ_k|o_k) P(λk∣ok)称为发射概率, P ( o k ∣ o k − 1 ) P(o_k|o_{k-1}) P(ok∣ok−1)称为转移概率。通过设置某些 P ( o k ∣ k 1 ) = 0 P(o_k|k_1)=0 P(ok∣k1)=0,可以排除类似BBB、EM等不合理的组合。
事实上,式(6) 的马尔可夫假设就是一个二元语言模型( bigram model ) , 当将齐次马尔可夫假设改为每个输出与前两个有关时,就变成了三元语言模型( trigram model ) 。当然在实际分词应用中还是多采用二元模型,因为相比三元模型,其计算复杂度要小不少。
在HMM 中,求解 m a x P ( λ ∣ o ) P ( o ) maxP(λ|o)P(o) maxP(λ∣o)P(o)的常用方法是Veterbi 算法。它是一种动态规划方法,核心思想是: 如果最终的最优路径经过某个 o i o_i oi, 那么从初始节点到 o i − 1 o_{i-1} oi−1点的路径必然也是一个最优路径一一因为每一个节点。i 只会影响前后两个 P ( o i − 1 和 P ( o i ∣ o i + 1 ) P(o_{i-1}和P(o_i|o_{i+1}) P(oi−1和P(oi∣oi+1)。
根据这个思想,可以通过递推的方法,在考虑每个0; 时只需要求出所有经过各 o i − 1 o_{i-1} oi−1的候选点的最优路径, 然后再与当前的 o i o_i oi 结合比较。这样每步只需要算不超过 l 2 l^{2} l2次,就可以逐步找出最优路径。Viterbi 算法的效率是 O ( n ⋅ l 2 ) O(n·l^{2}) O(n⋅l2), l l l是候选数目最多的节点 o i o_i oi的候选数目,它正比于n, 这是非常高效率的。HMM 的状态转移图如下图 所示。
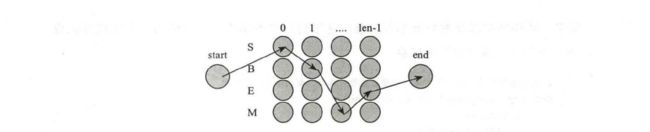
源码实现
# -*- coding: utf-8 -*-
__author__ = 'tan'
import os
import logging
import codecs
import pickle
import numpy as np
class HMMModel:
def __init__(self, N, M, PI, AA, BB):
self.n = N
self.m = M
self.pi = PI
self.B = BB
self.A = AA
def viterbi(self, T, O):
'''
下标都是从0开始的
:param T:
:param O:
:return:
'''
# 初始化
delta = np.zeros((T, self.n))
psi = np.zeros((T, self.n))
for i in range(self.n):
delta[0][i] = self.pi[i]*self.B[i][O[1]]
psi[0][i] = 0
# 递推
for t in range(1, T):
for i in range(self.n):
maxDelta = 0.0
index = 1
for j in range(self.n):
if maxDelta < delta[t-1][j] * self.A[j][i]:
maxDelta = delta[t-1][j] * self.A[j][i]
index = j
delta[t][i] = maxDelta * self.B[i][O[t]]
psi[t][i] = index
# 终止
prob = 0
path = [0 for _ in range(T)]
path[T-1] = 1
for i in range(self.n):
if prob < delta[T-1][i]:
prob = delta[T-1][i]
path[T-1] = i
# 最优路径回溯
for t in range(T-2, -1, -1):
path[t] = psi[t+1][path[t+1]]
return path, prob, delta, psi
class HMMSegment:
def __init__(self, dictfile="dict.utf8.txt"):
'''
:param dictfile: 词汇文件名
:return:
'''
self.word2idx = {}
self.idx2word = {}
self.hmmmodel = None
self.outfile = dictfile
self.inited = False
def build_dict_file(self, filename):
f = codecs.open(filename, "rb", encoding="utf-8")
idx = 1
words = {}
for line in f:
line = line.strip()
if len(line) == 0:
continue
idx += 1
if idx % 100 == 0:
print("read %d lines" % idx)
ws = line.split()
for word in ws:
for _, w in enumerate(word):
if w not in words:
words[w] = 0
words[w] += 1
f.close()
dicts = sorted(words.items(), key=lambda d:d[1], reverse=True)
print("writing the words in to file {}".format(self.outfile))
dictfile = codecs.open(self.outfile, "wb", encoding="utf-8")
for d in dicts:
dictfile.write("%s\t%d\n" % (d[0], d[1]))
dictfile.close()
def init_paramater(self, load=False, save=False):
'''
'''
if load == True:
self.word2idx = pickle.load(open("word2idx.pkl", "rb"))
self.idx2word = pickle.load(open("idx2word.pkl", "rb"))
else:
f = codecs.open(self.outfile, "rb", encoding="utf-8")
for idx, line in enumerate(f):
word, _ = line.strip().split("\t")
self.word2idx[word] = idx + 1
self.idx2word[idx+1] = word
f.close()
if save:
pickle.dump(self.word2idx, open("word2idx.pkl", "wb"))
pickle.dump(self.idx2word, open("idx2word.pkl", "wb"))
def init_model(self, trainfile=None, load=False, save=False):
self.init_paramater(load, save)
if load:
A = pickle.load(open("A.pkl", "rb"))
B = pickle.load(open("B.pkl", "rb"))
PI = pickle.load(open("PI.pkl", "rb"))
else:
f = codecs.open(trainfile, "rb", encoding="utf-8")
lines = f.readlines()
f.close()
PI, A, B = self.init_A_B_PI(lines)
if save:
pickle.dump(A, open("A.pkl", "wb"))
pickle.dump(B, open("B.pkl", "wb"))
pickle.dump(PI, open("PI.pkl", "wb"))
self.hmmmodel = HMMModel(4, len(self.word2idx), PI, A, B)
def init_A_B_PI(self, lines):
'''
* count matrix:
* ALL B M E S
* B * * * * *
* M * * * * *
* E * * * * *
* S * * * * *
*
* NOTE:
* count[2][4] is the total number of complex words
* count[3][4] is the total number of single words
:return:
:param lines:
:return:
'''
print("Init A B PI paramaters")
last = ""
countA = np.zeros((4, 5))
numwords = len(self.word2idx)
print(numwords)
countB = np.zeros((4, numwords+1))
for line in lines:
line = line.strip()
if len(line) == 0:
continue
phrase = line.split(" ")
for word in phrase:
# print(word)
word = word.strip()
num = len(word)
#只有一个单词 S 3
if num == 1:
#countB
countB[3][self.word2idx[word]] += 1
countB[3][0] += 1
########################
countA[3][4] += 1 # 单个词的个数
#统计转移值
if last != "":
#单独词转移过来 S -> S
if len(last) == 1:
countA[3][3] += 1
#是从词尾转移过来 E-> S
else:
countA[2][3] += 1
else:
countA[2][4] += 1 # 多个词的个数
countA[0][4] += 1 # B->任意 统计
if num > 2:
countA[0][1] += 1 # B -> M
countA[1][4] += num - 2 # 统计M转移的个数
if num > 3: # M-> M
countA[1][1] += num - 3
countA[1][2] += 1 # M->E
else:
countA[0][2] += 1 # B->E
if last != "":
if len(last) == 1:
countA[3][0] += 1 # S-> B
else:
countA[2][0] += 1 # E -> B
###countB 用于计算B矩阵
for idx, w in enumerate(word):
if idx == 0:
countB[0][self.word2idx[word[idx]]] += 1
countB[0][0] += 1
elif idx == num - 1:
countB[2][self.word2idx[word[idx]]] += 1
countB[2][0] += 1
else:
countB[1][self.word2idx[word[idx]]] += 1
countB[1][0] += 1
last = word
countA[2][0] += 1 # 最后一个E 设为E->B
print("The count matrix is:")
print(countA)
# print(countB)
A = np.zeros((4, 4))
PI = np.array([0.0] * 4)
B = np.zeros((4, numwords+1))
allwords = countA[2][4] + countA[3][4]
PI[0] = countA[0][4] / allwords
PI[3] = countA[3][4] / allwords
for i in range(4):
for j in range(4):
A[i][j] = countA[i][j] / countA[i][4]
for j in range(1, numwords+1):
B[i][j] = (countB[i][j] + 1) / countB[i][0]
print("A and PI B is ")
print(PI)
print(A)
# print(B)
return PI, A, B
def segment_sent(self, sentence):
if not self.inited:
self.init_model(load=True)
O = []
for w in sentence:
w = w.strip()
if len(w) == 0:
continue
if w not in self.word2idx:
num = len(self.word2idx)+1
self.word2idx[w] = num
self.idx2word[num] = w
#初始化未登录词的概率
self.hmmmodel.B = np.column_stack((self.hmmmodel.B, np.array([0.3, 0.3, 0.3, 0.1])))
O.append(self.word2idx[w])
T = len(O)
path, prob, delta, psi = self.hmmmodel.viterbi(T, O)
result = ""
for idx, p in enumerate(path):
# print(self.idx2word[O[idx]], end="")
result += self.idx2word[O[idx]]
if p == 2 or p == 3:
# print("/ ", end="")
result +="/ "
# print("")
# print(path)
# print(prob)
return result
def cut_sentence_new(self, content):
start = 0
i = 0
sents = []
punt_list = ',.!?:;~,。!?:;~'
for word in content:
if word in punt_list and token not in punt_list: #检查标点符号下一个字符是否还是标点
sents.append(content[start:i+1])
start = i+1
i += 1
else:
i += 1
token = list(content[start:i+2]).pop() # 取下一个字符
if start < len(content):
sents.append(content[start:])
return sents
def segment_sentences(self, content):
result = ""
sentences = self.cut_sentence_new(content)
for sent in sentences:
# print(sent)
result += self.segment_sent(sent)
# print(tmp)
# result += tmp
return result
if __name__ == "__main__":
traingfile = "trainCorpus.txt_utf8"
hmmseg = HMMSegment()
# hmmseg.init_model(traingfile, save=True)
hmmseg.init_model(traingfile, load=True)
sent = "我是在我在那,昆明理工大学"
# hmmseg.segment_sent(sent)
two = "辛辛苦苦做的敲个代码还是错的,我好难呀"
# hmmseg.segment_sent(two)
content = u'''我是谁,我在那,敲个代码还是错的,我好难那'''
print(hmmseg.segment_sentences(content))
# hmmseg.build_dict_file(traingfile)
# lines = ["abc a ab", "abc a a ab abcd"]
# hmmseg.init_A_B_PI(lines)
# hmmseg.init_B(lines)
2.3 混合分词
事实上,目前不管是基于规则的算法、还是基于HMM 、CRF或者deep learning 等的方法,其分词效果在具体任务中,其实差距并没有那么明显。在实际工程应用中,多是基于一种分词算法, 然后用其他分词算法加以辅助。最常用的方式就是先基于词典的方式进行分词,然后再用统计分词方法进行辅助。如此,能在保证词典分词准确率的基础上,对未登录词和歧义词有较好的识别。
三、中文分词工具
随着NLP技术的发展,开源实现的分词工具越来越多,比如:Jieba、Ansj、盘古分词等,除此之外,由北大发布的开源分词工具PKUSeg效果也是特别的不错。网上分词工具的案例也特别多,就不过多细节介绍了。
四、参考链接
1、https://blog.csdn.net/qxdoit/article/details/83063794
2、https://blog.csdn.net/lalalawxt/article/details/75458791
3、https://blog.csdn.net/lilong117194/article/details/81113171
4、https://kexue.fm/archives/3922
5、https://blog.csdn.net/sinat_33741547/article/details/78870575
五、源码获取
文中涉及的源码及文件获取链接:https://github.com/jiajikang1993/NLP_related_algorithm_learned/tree/master/NLP%20related%20algorithm%20learning


