强化学习实践笔记（1）——Q-learning、SARSA和SARSA(lambda)

概述

本文介绍了单步Q-learning和SARSA的原理和python实现，还有基于eligibility trace的SARSA($\lambda$)算法。（算法原理部分是大致看完sutton书中对应小节之后的一些总结，实现的部分均按照莫烦强化学习中前几节课的算法代码部分重新敲了一遍，真的是特别好的学习材料！）

这几种方法均属于TD(Temporal Difference)算法，均为无模型的算法，其中Q-learning的方法属于on-policy（在线学习）的方法，SARSA属于off-policy（离线学习）的方法，而SARSA($\lambda$)是在SARSA的基础上与eligibility trace的结合，以提高算法收敛速度。

有任何不足之处，望指正！

1. Q-learning 算法原理及实现

1.1 TD算法的优势

首先，TD算法相对于蒙特卡洛算法和动态规划方法都有优势的，也可以说TD算法结合了这两种算法的优势，TD相对于蒙特卡洛算法的优势在于它不需要等到每次回合结束才能够更新动作值或状态值表（e.g. Q table）；而TD算法相对于动态规划的优势在于它不需要一个环境模型（因为动态规划算法的更新规则默认与智能体交互的环境模型已知，即状态转移概率完全已知，当然大部分情况下是不现实的。）

其次，TD算法的收敛性在理论上也是有保证的。在Sutton的书中也提到：“如果步长参数是一个足够小的常数，对于任何策略$\pi$, TD(0)中对状态值的估计的均值能够收敛到$v_{\pi }$。如果该参数能够同时满足以下两个条件，$$\sum _{n=1}^{\infty }{\alpha }_n(a)=\infty$$$$\sum _{n=1}^{\infty }{\alpha }_n^2(a)<\infty$$，则该值能够依概率1收敛。”

1.2 Q-learning 相对于TD(0)的变化

由TD算法引出SARSA这种在线学习的方法是很自然的，合逻辑的顺序应该是先SARSA, 后Q-learning。

TD(0)主要是针对状态值（$v_{\pi }(s)$）提出的一类算法，也就是书中所提到的预测问题，即预测某一个状态的状态值，而Q-learning算法和SARSA算法都是将对状态值的预测替换成对动作值（$q_{\pi }(s,a)$）的预测，我想其中的原因应该在于一般情况下的状态值是动作值的期望，而在强化学习过程中，我们获得的经验轨迹（trajectory）当中含有具体的某个状态和具体智能体做出的某个动作，所以对智能体的动作值进行估计是比较合理的。

1.3 Q-learning算法伪代码

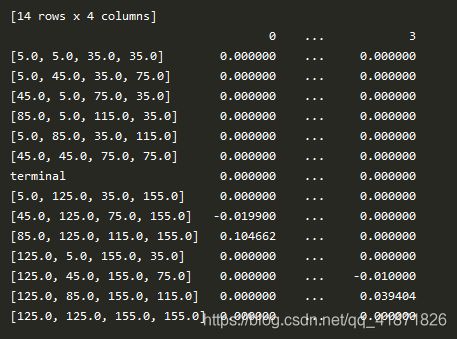
该算法在实现过程中使用的数据结构就是二维数组了，使用的也是数组的基本操作，存储和访问。只不过第一维的标签为状态S，实现的过程中用字符串描述（具体来说是list到string的转换），第二维的标签为动作A（这里学习的是离散的动作，所以每个动作都有对应的具体整数值，比如[0,1,2,3,4]分别代表了5个动作），并且在实现过程中Q表的构建使用了python pandas库中的pandas.DataFrame。

伪代码中标红的部分我觉得是Q-learning中最核心的语句，从中体现了Q-learning离线学习的本质。Q-learning的动作选择策略采用的是$ϵ-greedy$的策略，而在学习的过程中（即对Q表进行更新的过程中使用的策略是在某个状态下，选取最大化Q值的动作）用以下这个简单的例子可以具体说明：

假设我们总共有三个动作：$a_1,a_2,a_3$，在$ϵ-greedy$策略下，我们恰好进行了随机选择，假设在这轮迭代中我们选择了$a_3$，而在Q表中这些动作对应的Q值的大小关系满足$Q(s,a_1)>Q(s,a_2)>Q(s,a_3)$，在更新的过程中，Q表会按照$a_1$的动作进行更新，与一开始所选择的动作$a_3$是不一致的，这就是离线学习。

Q表的输出如下：
每一行代表一个状态，每一列代表动作。

1.4 Q-learning实现

这部分我只贴上智能体的代码，用tkinter编写的环境部分的代码还没来得及仔细看，但莫烦教程中的接口与gym的API保持一致。其余代码可以参考其莫烦个人主页

import tkinter as tk
import numpy as np
import time
import sys

import pandas as pd
# 以下注释为测试pandas中的DataFrame
# table = pd.DataFrame(1, columns=['u','d','l','r'],index=[1,2,3,4], dtype=np.float64)
# table = pd.DataFrame({'one':[1,2,3,4], 'two':[9,8,7,6]}, index=['a','b','c','d'])
# print('the max of this table: {}'.format(np.max(table)), '\n')
# list = pd.Series(10, index=[i for i in range(4)])
# list = table.loc['a']
# print(list == np.max(list), '\n') # np.max() returns the maximum value of this list
# print(list[list == np.max(list)].index)
# print(list[list == np.max(list)].index
# actions = ['u', 'd', 'l', 'r']
# print(np.random.choice(actions))
# state = 'e'
# c = pd.Series([0]*2, index=table.columns, name=state)
# print(c)
# table = table.append(pd.Series([0]*2, index=table.columns, name=state))
# print(table)

class QLearningTable(object):
    def __init__(self, actions, learning_rate=0.01, gamma=0.9, e_greedy=0.9):
        self.actions = actions
        self.lr = learning_rate
        self.gamma = gamma
        self.epsilon = e_greedy
        # initialize the table for storing Q value of each state-action pair
        self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64)

    def choose_action(self, state): # use epsilon greedy to choose action
        self.check_state_exist(state)
        if np.random.uniform() < self.epsilon:
            all_actions = self.q_table.loc[state, :] # all action values in this state
            # choose the max action
            action = np.random.choice(all_actions[all_actions == np.max(all_actions)].index)
        else:
            action = np.random.choice(self.actions)
        return action

    def learn(self, s, a, r, s_): # update the q table, the core of Q-learning
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, :].max()
        else:
            q_target = r
        self.q_table.loc[s,a] += self.lr * (q_target - q_predict)

    def check_state_exist(self, state):
        if state not in self.q_table.index:
            self.q_table = self.q_table.append(
                pd.Series(
                    [0] * len(self.actions),
                    index=self.q_table.columns,
                    name=state
                )
            )

2. SARSA算法原理及实现

2.1 SARSA与Q-learning的区别

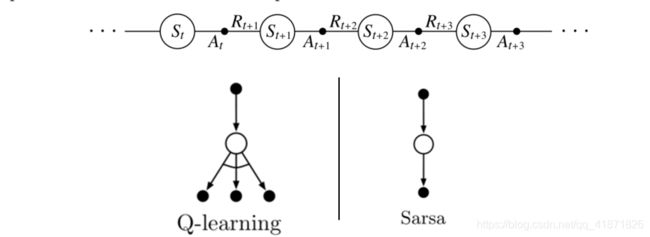
上图最上方是某一幕下获得的状态动作轨迹，下图则是Q-learning和SARSA算法的回溯图（Back-up Diagram），其中Q-learning在最后是取不同动作对应的最大值，SARSA则是按照当前策略选取动作后，用该动作将会“指引”智能体到达的下一个状态（$s^{\prime }$）和在该状态下再次根据策略所获取的下一个动作（$a^{\prime }$），利用以上这两种信息对Q表进行更新，这也是SARSA算法名称的由来，State-Action-Reward-State-Action。

2.2 SARSA算法伪代码

还是用前文Q-learning中的例子来解释伪代码中标红的部分：

假设我们总共有三个状态：$s_1,s_2,s_3$，和三个动作：$a_1,a_2,a_3$，且当前状态为$s_1$，在$ϵ-greedy$策略下，我们恰好进行了随机选择，假设在这轮迭代中我们选择了$a_3$，该动作使智能体观测到了环境的下一个状态，假设为$s_2$，在$s_2$状态下继续根据动作选择策略获取到动作为$a_2$，则在Q表更新中的公式为：
$$Q(s_1,a_3)\leftarrow Q(s_1,a_3)+\alpha [R+\gamma Q(s_2,a_2)-Q(s_1,a_3)]$$
这就是所谓的在线学习。

2.3 SARSA实现

这部分就之贴上与Q-learning程序中不一样的地方，首先是整体的运行框架多了下一个状态的相关语句，如下:

from maze_env import Maze
from test_RL import Sarsa

def update():
    for episode in range(100):
        s = env.reset()
        # print(type(s))
        a = sarsa.choose_action(str(s))
        while True:
            env.render()

            s_, r, done = env.step(a)
            a_ = sarsa.choose_action(str(s_))
            sarsa.learn(str(s),a,r,str(s_), a_)
            s = s_
            a = a_
            if done:
                break

if __name__ == '__main__':
    env = Maze()
    sarsa = Sarsa(actions=list(range(env.n_actions)))

    env.after(100, update)
    env.mainloop()

这里的sarsa.learn与之前的Q-learning不太一样，多了下一个动作（a_）这个变量。

	...
    def learn(self,s, a, r, s_, a_): # update the sarsa table
        self.check_state_exist(s_)
        q_predict = self.sarsa_table.loc[s,a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.sarsa_table.loc[s_, a_]
        else:
            q_target = r
        self.sarsa_table.loc[s,a] += self.lr * (q_target - q_predict)

3. SARSA($\lambda$)原理及实现

3.1 SARSA($\lambda$)伪代码

3.2 SARSA($\lambda$)与SARSA算法的区别

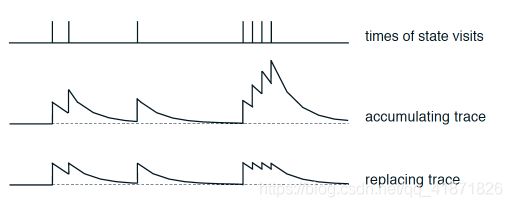
SARSA($\lambda$)算法是在SARSA算法的基础上引入了资格迹（eligibility trace），直观上解释就是让算法对于经历过的状态有一定的记忆性，如sutton书中所述，资格迹对所获取的轨迹起到了短期记忆的效果。从下图可以直观看出，经历过的状态不再是经历过之后直接删除，而是存在一个平滑的衰减过渡，保存了一定程度上的信息。也可以说，该算法增加了距离目标点最近的状态的权重，从而加快算法的收敛性（直观意义上的说法）。

3.3 SARSA($\lambda$)实现

与SARSA代码不同的地方也是在learn函数，这里需要再引入一个与Q表相同维度大小的表，用于表示eligbiltiy trace（下文用E表来表示），在检查已有Q表中是否有某个状态的时候，也需要对E表进行检查，如果没有对应状态，需要调用append函数。

    def learn(self, s, a, r, s_, a_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, a_]  # next state is not terminal
        else:
            q_target = r  # next state is terminal
        error = q_target - q_predict

        # increase trace amount for visited state-action pair

        # Method 1:
        # self.eligibility_trace.loc[s, a] += 1

        # Method 2:
        self.eligibility_trace.loc[s, :] *= 0
        self.eligibility_trace.loc[s, a] = 1

        # Q update
        self.q_table += self.lr * error * self.eligibility_trace

        # decay eligibility trace after update
        self.eligibility_trace *= self.gamma*self.lambda_