强化学习入门4—Q-learning和Sarsa
目录
- 时序差分TD
-
- Q-Learning
-
- 算法流程
- Sarsa
-
- 算法流程
- 小结
本文是强化学习入门系列的第4篇,主要介绍强化学习当中非常常见的两个时序差分算法:Q-learning和Sarsa。
时序差分TD
首先,啥是时序差分学习?
时序差分学习可以直接从与环境互动的经验中学习策略,无需构建关于环境动态特性的模型,也就是常说的model-free方法。像上文的动态规划方法就需要已知环境的动态特性,属于model-based方法。
时序差分学习利用经验来解决预测。也就是说需要根据给定策略学习来的一些经验数据,来对状态价值函数 V π V_{\pi} Vπ 进行更新。
本文介绍两种经典的时序差分学习方法,Q-learning和Sarsa。
Q-Learning
Q-Learning是一种off-policy的算法,它可以学习当前的数据也可以学习过去的数据。
如何学习?
首先是有个Q-table,通过迭代来对表进行更新。Q-learning的核心在于它有一张Q表格,所有的value更新都是在这张表格上进行的。表格储存了历史的数据,所以Q-learning不仅可以学习当前的数据,也可以学习过去经历的数据。
举个例子
假设现在有3个状态,每个状态有3个动作,假设动作 a 1 a_1 a1 对应的奖励为 +1, a 2 a_2 a2 对应的奖励为 -1, a 3 a_3 a3 对应的奖励为0。那Q表可以用矩阵来表示。
首先是初始化Q表,每个Q值也就是动作价值初始为0。
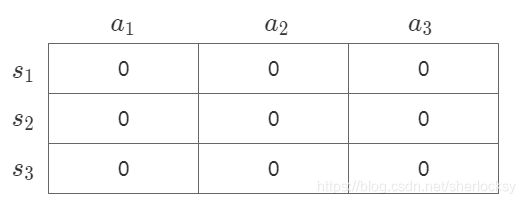
第一步:决策。
假设初始状态是 s 1 s_1 s1。根据 ϵ − g r e e d y \epsilon-greedy ϵ−greedy 策略选取动作,由于初始Q值都是0,所以这时候就是随机选取,假设选择了动作 a 1 a_1 a1,进入到 s 2 s_2 s2,奖励是+1,此时根据更新公式:
Q ( s , a ) ← Q ( s , a ) + α [ r + γ max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s,a)\leftarrow Q(s,a)+\alpha[r+\gamma \max_{a'}Q(s',a')-Q(s,a)] Q(s,a)←Q(s,a)+α[r+γa′maxQ(s′,a′)−Q(s,a)]
第二步:更新Q值。
我们假设学习率是1,折扣系数 γ \gamma γ 为0.8。那么 Q ( s 1 , a 1 ) Q(s_1,a_1) Q(s1,a1) 的值应该更新为 0 + ( 1 + 0.8 × 0 − 0 ) = 1 0+(1+0.8\times0-0)=1 0+(1+0.8×0−0)=1,Q表也更新如下:
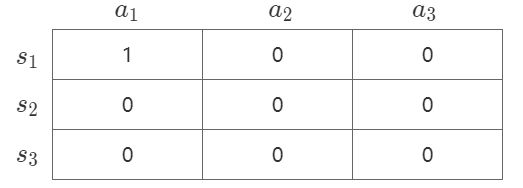
这样就完成了一次更新。可以发现,Q-learning是属于单步更新。
接下来的步骤跟上面是一样,如此迭代,更新,就是Q-learning。
算法流程
在选择动作的策略上,基于epsilon-greedy的方法从当前状态选择价值最大的动作a。
Q值如何更新?
在Q表的更新上,动作a产生的奖励r,以及下一状态s’,但下一状态s’上的动作使用的是max值来进行update。
值得注意的是,因为max这个操作,使得Q-learning不适用于连续动作问题。
Sarsa
Sarsa是属于on-policy算法。它只能学习当前的数据。
如何学习?
Sarsa算法与Q-learning相似,Sarsa也有一个Q表,在对动作的选择也就是决策部分与Q-learning是一样的。
不同的是在Q值的更新上,Q-learning中对下一个状态和动作采取的是max的操作,比较贪婪,而Sarsa则相对保守,在更新 Q ( s , a ) Q(s,a) Q(s,a) 时基于的是下一个 Q ( s ′ , a ′ ) Q(s',a') Q(s′,a′)。
两个算法都用了epsilon-greedy来选择action。但是,Sarsa 是在learn之前是用epsilon-greedy选中一个action,并确定用这个action进行learn,所以下一步update的action就是要learn的action。所以当前learn的不一定是最大奖励的。而Q-learning对下一步的action取max,每步learn的都是眼前奖励最大的,但由于epsilon-greedy存在随机性,可能会跳出贪心,转变为随机选择,所以下一步update的action大概率不是要learn的。
接Q-learning的例子
我们沿用上面例子的setting,假设现在的Q表如下:

假设当前时刻状态是 s 1 s_1 s1,选择了动作 a 1 a_1 a1,进入到了下一时刻状态 s 2 s_2 s2,然后下一时刻的 s 2 s_2 s2 状态下根据贪心策略选择了动作 a 3 a_3 a3 。
那么,在更新Q值的时候,因为Sarsa是要考虑下一时刻的 ( s ′ , a ′ ) (s',a') (s′,a′) 的,也就是 ( s 2 , a 3 ) (s_2,a_3) (s2,a3),所以根据公式:
Q ( s , a ) ← Q ( s , a ) + α [ r + γ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s,a)\leftarrow Q(s,a)+\alpha[r+\gamma Q(s',a')-Q(s,a)] Q(s,a)←Q(s,a)+α[r+γQ(s′,a′)−Q(s,a)]
Q ( s 1 , a 1 ) Q(s_1,a_1) Q(s1,a1) 的值应该更新为 2 + ( 1 + 0.8 × 2 − 2 ) = 2.6 2+(1+0.8\times 2-2)=2.6 2+(1+0.8×2−2)=2.6,
而如果是Q-leaning,对 s 2 s_2 s2 下的Q值取最大值,那就是 ( s 2 , a 1 ) (s_2,a_1) (s2,a1),此时的更新则是 2 + ( 1 + 0.8 × 4 − 2 ) = 4.2 2+(1+0.8\times 4-2)=4.2 2+(1+0.8×4−2)=4.2。
算法流程
伪代码如下:

Sarsa因为更新的时候考虑的连续时刻的值,所以Sarsa适用于连续性问题。
小结
Q-learning和Sarsa一个是off-policy算法,一个是on-policy算法。两者在算法上的区别就在于Q值更新的不同。换句话说,Q-learning在下一步更新时,考虑的是下一时刻中的最大Q值,而Sarsa是即时更新,在更新的时候,只考虑下一时刻的Q值。
参考
- 什么是 Q Leaning - 强化学习 (Reinforcement Learning) | 莫烦Python (mofanpy.com)
- 什么是 Sarsa - 强化学习 (Reinforcement Learning) | 莫烦Python (mofanpy.com
- DQN从入门到放弃5 深度解读DQN算法
