感知器【python】

1. 实验目的

1.理解感知器的基本原理
2.提高基础编程能力

2. 实训内容

例子：用感知器实现or函数

0 表示false， 1表示true

3. 感知器原理

感知器（perceptron）是人工神经网络中最基础的网络结构（perceptron一般特指单层感知器），单层感知器的模型，公式为

其中X代表向量[x1,x2,…,xn,1]，W代表向量[w1,w2,…,wn,b]，σ代表激活函数

对于一组输入值X，我们期望该网络的输出值为Y，而实际输出值为y，则我们定义损失函数（或者称为代价函数、目标函数）L为：

其中的X和Y已知，L是关于W的函数。对此可通过梯度下降法(先确定一个初始值，然后将W沿着梯度下降的方向进行调整，就会使得L的值向更小的方向进行变化)改变W，使得L等于0或者无线趋近于0，则此时可以认为网络的输出值y就等于期望值Y。

4. 代码方法和步骤

4.1 向量的计算

向量内积计算dot(x, y)
将x[x1, x2, x3...]和y[y1, y2, y3...]按元素对应相乘【调用两个向量x和y按元素相乘方法element_multiply(x, y)】，即转变为[x1 * y1, x2 * y2, x3 * y3 …]
使用reduce()函数【对参数序列中元素进行累积求和0】

@staticmethod
def dot(x, y):
    return reduce(lambda a, b: a + b, VectorOp.element_multiply(x, y), 0.0)
	向量按元素相乘element_multiply(x, y)
	将x[x1, x2, x3...]和y[y1, y2, y3...]通过zip()打包在一起，变成[(x1,y1),(x2, y2),(x3,y3),...]
	利用map 函数计算[x1*y1, x2*y2, x3*y3]
	list（）返回列表集合
@staticmethod
def element_multiply(x, y):         
    return list(map(lambda x_y: x_y[0] * x_y[1], zip(x, y)))
4.1.3向量x和y按元素相加element_add(x, y)
	将x[x1, x2, x3...]和y[y1, y2, y3...]通过zip()打包在一起, 变成[(x1,y1),(x2, y2),(x3,y3),...]
	利用map 函数计算[x1+y1, x2+y2, x3+y3]
	通过list()返回一个列表
@staticmethod
def element_add(x, y):
    return list(map(lambda x_y: x_y[0] + x_y[1], zip(x, y)))

4.1.4某向量中的每个元素和标量相乘scala_multiply(v, s)

将向量v中的每个元素和标量s相乘

@staticmethod
def scala_multiply(v, s):
    return map(lambda e: e * s, v)

4.2.感知器

4.2.1初始化感知器__init__

初始化感知器 ，设置输入参数的个数input_num [初始权重0.0，初始偏置项0.0]

def __init__(self, input_num, activator):
self.activator = activator
    weight=int(input("初始化权重"))
    self.weights = [weight] * input_num
    print("初始化权重为",self.weights)
    self.bias = 0.0

4.2.2训练(多次迭代)

输入训练数据：一组向量input_vecs、以及每个向量对应的标签labels、以及迭代次数iteration和学习率rate
使用for循环迭代次数

def train(self, input_vecs, labels, iteration, rate):
	for i in range(iteration):
        self._one_iteration(input_vecs, labels, rate)

4.2.3 单次迭代_one_iteration

把输入input_vecs和输出labels通过zip()打包在一起，生成样本列表samples【包含每个样本(samples)均为（input_vec, label）】
循环预测每个输入(input_vec)定义output输出
将预测输出output和输入input_vec，和真实输出标签label以及学习率用于权重更新学习

def _one_iteration(self, input_vecs, labels, rate):
	samples = zip(input_vecs, labels)
    for (input_vec, label) in samples:
        output = self.predict(input_vec)
        self._update_weights(input_vec, output, label, rate)

4.2.4更新权重_update_weights

计算本次更新的delta(梯度变化)
input_vec[x1, x2, x3,...]向量中的每个值乘上delta*学习率
通过element_add向量相加把权重更新按元素加到原先的weights[w1, w2, w3,...]上

def _update_weights(self, input_vec, output, label, rate):
	delta = label - output
    self.weights = VectorOp.element_add(
    self.weights, VectorOp.scala_multiply(input_vec, rate * delta))
    self.bias += rate * delta

4.2.5预测predict

通过输入，权重，偏置进行向量内积计算返回感知器

def predict(self, input_vec):
	return self.activator(
          VectorOp.dot(input_vec, self.weights) + self.bias)

4.3激活函数

采用激活函数【如果x大于0则返回1，否则返回0】

def f(x):
	return 1 if x > 0 else 0

	训练数据get_training_dataset()

根据or真值表产生训练数据

def get_training_dataset():
	input_vecs = [[0, 0], [0, 1], [1, 0], [1, 1]]
  labels = [0, 1, 1, 1]
  return input_vecs, labels

训练感知器train_and_perception()
输入迭代次数num
通过get_training_dataset()函数获取训练集
开始训练train()

def train_and_perception():
p = Perceptron(2, f)
  num=int(input("迭代次数"))
  input_vecs, labels = get_training_dataset()
  p.train(input_vecs, labels, num, 0.1)
  return p

5. 不同迭代次数，不同初始化权重对结果的影响

当初始化权重为大于0时，不同的迭代次数均不会对偏置项结果产生改变[由于所给训练集的缘故]

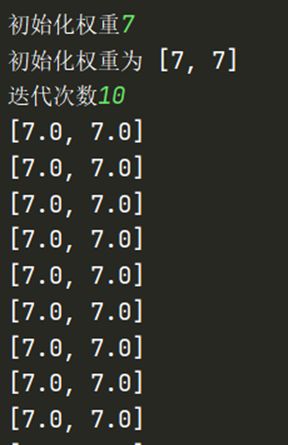
当初始化权重为小于0时，不同的初始化权重以及不同的迭代次数会对偏置项结果产生不同的变化

不同的初始化权重(-1至-1000)，相同发迭代次数5情况下测试得
(初始化权重,偏置项)=》[（-1，0.7),（-2，1.1)，（-3，1.1)，（-4，1.1)…………（-1000，1.1)] 随着初始化权重减小，偏置项改变直至稳定某数
不同发迭代次数，相同的初始化权重情况下测试得
(初始化权重,偏置项)=》（-5，0.3),（-5，0.5)，（-5，0.7)，（-5，0.9)，（-5，1.1)…(-5,1.0)…(-5,-0.0),(-5,-0.0),(-5,-0.0) 随着迭代次数增加，偏置项改变直至稳定至-0.0

6.完整代码

from __future__ import print_function
from functools import reduce

# 实现向量计算
class VectorOp(object):

    @staticmethod
    def dot(x, y):
        return reduce(lambda a, b: a + b, VectorOp.element_multiply(x, y), 0.0)

    @staticmethod
    def element_multiply(x, y):
        return list(map(lambda x_y: x_y[0] * x_y[1], zip(x, y)))

    @staticmethod
    def element_add(x, y):
        return list(map(lambda x_y: x_y[0] + x_y[1], zip(x, y)))


    @staticmethod
    def scala_multiply(v, s):
        return map(lambda e: e * s, v)
    # 将向量v中的每个元素和标量s相乘

class Perceptron(object):
    def __init__(self, input_num, activator):
        self.activator = activator
        weight=int(input("初始化权重"))
        self.weights = [weight] * input_num
        print("初始化权重为",self.weights)
        self.bias = 0.0
    # 初始化感知器，设置输入参数的个数，以及激活函数。
    def __str__(self):
        #   打印学习到的权重、偏置项
        return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias)

    def train(self, input_vecs, labels, iteration, rate):
        for i in range(iteration):
            self._one_iteration(input_vecs, labels, rate)
    # 输入训练数据：一组向量、以及每个向量对应的label；以及迭代次数和学习率
    def _one_iteration(self, input_vecs, labels, rate):
        samples = zip(input_vecs, labels)
        for (input_vec, label) in samples:
            output = self.predict(input_vec)
            self._update_weights(input_vec, output, label, rate)

    def _update_weights(self, input_vec, output, label, rate):
        delta = label - output
        self.weights = VectorOp.element_add(
        self.weights, VectorOp.scala_multiply(input_vec, rate * delta))
        print(self.weights)
        self.bias += rate * delta
    def predict(self, input_vec):
          return self.activator(
              VectorOp.dot(input_vec, self.weights) + self.bias)

# 定义激活函数
def f(x):
  return 1 if x > 0 else 0
# 根据or真值表产生训练数据
def get_training_dataset():
  input_vecs = [[0, 0], [0, 1], [1, 0], [1, 1]]
  labels = [0, 1, 1, 1]
  return input_vecs, labels
# 使用or真值表训练感知器
def train_and_perception():
  p = Perceptron(2, f)
  num=int(input("迭代次数"))
  input_vecs, labels = get_training_dataset()
  p.train(input_vecs, labels, num, 0.1)
  return p

and_perception = train_and_perception()
print(and_perception)

7.nice~~~~~~~~~~呀呀呀