TensorFlow:神经网络实现手写体数字识别
0,引言
MNIST 是一个非常有名的手写体数字识别数据集,在很多资料中,这个数据集都会被用作深度学习的入门样例。本文将介绍利用神经网络技术解决在MNIST数据集上的手写体数字识别问题。代码主要参考郑泽宇等著《TensorFlow实战Google 深度学习框架》一书(MNIST数据集下载地址https://download.csdn.net/download/u013419318/10833617)。
1,环境配置
(1)PyCharm Edition(下载地址:http://www.jetbrains.com/pycharm/)
(2)TensorFlow(下载地址:https://www.cnblogs.com/lvsling/p/8672404.html)
2,实现过程
(1)源代码
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
# MNIST数据集相关的常熟
INPUT_NODE = 784 # 输入层的节点数。对于MNIST数据集,这个就等于图片的像素
OUTPUT_NODE = 10 # 输出层的节点数。这个等于类别的数目。因为在MNIST数据集
# 中需要区分的是0~9这10个数字,所以这里输出层的节点数为10
# 配置神经网络的参数
LAYER_NODE = 500 # 隐藏层节点数。这里使用的只有一个隐藏层的网络结构作为样例。
# 这个隐藏层有500个节点。
BATCH_SIZE = 100 # 一个训练batch中的训练数据个数。数字越小时,
# 训练过程越接近随机梯度下降;数字越大时,训练越接近梯度下降
LEARNING_RATE_BASE = 0.8 # 基础的学习率
LEARNING_RATE_DECAY = 0.99 # 学习率的衰减
REGULARIZATION_RATE = 0.0001 # 描述模型复杂度的正则项在损失函数中的系数。
TRAINING_STEPS = 30000 # 训练轮数。
MOVING_AVERAGE_DECAY = 0.99 # 滑动平均衰减率。
# 一个辅助函数,给定神经网络的输入和所有的参数,计算神经网络的前项传播结果。在这里
# 定义了一个使用ReLU激活函数的三层全连接网络。通过加入隐藏层实现了多层网络结构,
# 通过ReLU激活函数实现了去线性化。在这个函数中也支持传入用于计算参数平均值的类,
# 这样方便在测试的时候使用滑动平均模型。
def inference(input_tensor, avg_class, weights1, biases1, weights2, biases2):
# 当没有提供滑动平均类时,直接使用参数当前的取值。
if avg_class ==None:
# 计算隐藏层的前项传播结果,这里使用了ReLU激活函数。
layer1 = tf.nn.relu(tf.matmul(input_tensor, weights1) + biases1)
# 计算输出层的前项传播结果,因为计算损失函数时候会一并计算softmax函数,
# 所以这里不需要加入激活函数。而且不加入softmax不会影响预测结果。
# 因为预测时使用的是不同的类别对应节点输出的相对大小,有没有softmax层
# 对最后的分类结果的计算没有影响。于是在计算整个神经网络的前项传播时可以不加入最后的softmax层。
return tf.matmul(layer1, weights2) + biases2
else:
# 首先使用avg_class.average函数来计算得出的变量的滑动平均值。
# 然后再计算相应的神经网络的前项传播结果。
layer1 = tf.nn.relu(tf.matmul(input_tensor, avg_class.average(weights1)) + avg_class.average(biases1))
return tf.matmul(layer1, avg_class.average(weights2)) + avg_class.average(biases2)
# 训练模型的过程。
def train(mnist):
x = tf.placeholder(tf.float32, [None, INPUT_NODE],name='x-input')
y_ = tf.placeholder(tf.float32,[None, OUTPUT_NODE],name='y-input')
# 生成隐藏层的参数。
weights1 = tf.Variable(tf.truncated_normal([INPUT_NODE,LAYER_NODE],stddev=0.1))
biases1 = tf.Variable(tf.constant(0.1,shape=[LAYER_NODE]))
# 生成输出层的参数。
weights2 = tf.Variable(tf.truncated_normal([LAYER_NODE,OUTPUT_NODE],stddev=0.1))
biases2 = tf.Variable(tf.constant(0.1,shape=[OUTPUT_NODE]))
# 计算在当前参数下神经网络前项传播的结果。这里给出的用于计算滑动平均的类为None,
# 所以函数不会使用参数的滑动平均值。
y = inference(x,None,weights1, biases1, weights2, biases2)
# 定义储存训练轮数的变量。这个变量不需要计算滑动平均值,所以这里指定这个变量为
# 不可训练的变量(trainable = False)。在使用TensorFlow训练神经网络的时候,
# 一般会将代表训练轮数的变量指定为不可训练的参数。
global_step = tf.Variable(0, trainable=False)
# 给定滑动平均衰减率和训练轮数的变量,初始化滑动平均类。
# 在第4章中介绍过给定训练轮数的变量可以加快训练早期变量的更新速度。
variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
# 在所有神经网络参数的变量上使用滑动平均。其他辅助变量(比如global_step)就不需要了。
# tf.trainable_variable返回的就是图上的集合
# GraphHeys.TRAINABLE_VARIABLES中的元素。这个集合的元素就是所有没有指定trainable = False的参数。
variable_averages_op = variable_averages.apply(tf.trainable_variables())
# 计算使用了滑动平均之后的前项传播结果。第4章中介绍过滑动平均不会改变变量本身的取值,
# 而是会维护一个影子变量来记录起滑动平均值。所以当需要使用这个滑动平均值的时候,需要
# 明确调用average函数。
average_y = inference(x, variable_averages, weights1, biases1, weights2, biases2)
# 计算交叉熵作为刻画顶训值和真实值之间差距的损失函数。这里使用了TensorFlow 中提
# 供的sparse_softmax_cross_entropy_with_logits 函数来计算交叉熵。当分类
# 问题只打一个正确答案时,可以使用这个函数来加速交叉熵的计算。MNIST问题的图片中
# 只包含了0~9中的-个数字,所以可以使用这个函数来计算交叉熵损失。这个函数的第一个
# 参数是神经网络不包括softmax层的前向传播结果, 第二个是训练数据的正确答案。因为
# 标准答案是一个长度为10的一维数组,而该函数需要提供的是一个正确答案的数字,所以需
# 要使用tf.argmax函数来得到正确答案对应的类别编号。
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y,labels=tf.argmax(y_,1))
# 计算在当前batch中所有样例的交叉熵平均值。
cross_entropy_mean = tf.reduce_mean(cross_entropy)
# 计算L2正则化损失函数。
regularizer = tf.contrib.layers.l2_regularizer(REGULARIZATION_RATE)
# 计算模型的正则化损失。一般只计算神经网络边上权重的正则化损失,而不是使用偏置项。
regularizqtion = regularizer(weights1) + regularizer(weights2)
# 总损失等于交叉熵损失和正则化损失的和。
loss = cross_entropy_mean + regularizqtion
# 设置指数衰减的学习率。
learning_rate = tf.train.exponential_decay(
LEARNING_RATE_BASE, # 基础的学习率,随着迭代的进行,更新变量时使用的
# 学习率在这个基础上递减。
global_step, # 当前迭代的轮数。
mnist.train.num_examples / BATCH_SIZE, # 过完所有的训练数据需要的迭代次数。
LEARNING_RATE_DECAY) # 学习率衰减速度。
# 使用tf.train.GradientDescentOptimizer 优化算法来优化损失函数。注意这里损失函数
# 包含了交叉熵损失和12正则化损失。
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step)
# 在训练、神经网络模型时,每过一遍数据既需要通过反向传播来更新神经网络中的参数,
# 又要更新每一个参数的滑到J平均值。为了一次完成多个操作, TensorFlow 提供了
# tf.control dependencies 和tf.group 两种机制。下面两行程序和
# (train_op = tf . group(train_step, variables_averages_op)是等价的
with tf.control_dependencies([train_step, variable_averages_op]):
train_op = tf.no_op(name='train')
# 检验使用了滑动平均模型的神经网络前向传播结果是否正确。tf.argmax(average_y , 1)
# 计算每一个样例的预测答案。其中average_y 是一个batch_size 食10 的二维数组,每一行
# 表示一个样例的前向传播结果。tf . argmax 的第二个参数" l ”表示选取最大值的操作仅在第一
# 个维度中进行,也就是说,只在每一行选取最大值对应的下标。于是得到的结果是一个长度为
# batch 的一维数组,这个一维数组中的值就表示了每一个样例对应的数字识别结果。tf.equal
# 判断两个张量的每一维是否相等,如果相等返回True ,否则返回False 。
correct_prediction = tf.equal(tf.argmax(average_y,1), tf.argmax(y_,1))
# 这个运算首先将一个布尔型的数值转换为实数型,然后计算平均值。这个平均值就是模型在这
# 一组数据上的正确率。
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
# ****************************
list_test_acc = []
# ****************************
# 初始化会话并开始训练过程。
with tf.Session() as sess:
tf.global_variables_initializer().run()
# 准备验证数据。一般在神经网络的训练过程中会通过验证数据来大致判断停止的
# 条件和评判训练的效果。
validate_feed = {x:mnist.validation.images,y_:mnist.validation.labels}
# 准备测试数据。在真实的应用中,这部分数据在训练时是不可见的,这个数据只是作为模
# 型优劣的最后评价标准。
test_feed = {x:mnist.test.images,y_:mnist.test.labels}
# 法代地训练神经网络。
for i in range(TRAINING_STEPS):
# 每1000 轮输出一次在验证数据集上的测试结果。
if i % 1000 == 0:
# 计算滑动平均模型在验证数据上的结果。因为MNIST 数据集比较小,所以一次可以处理所有的验证数据。
# 为了计算方便,本样例程序没有将验证数据划分为更小的batch. 当神经网络棋型比较复杂或者验证数据
# 比较大时,太大的batch会导致计算时间过长甚至发生内存溢出的错误。
validate_acc = sess.run(accuracy, feed_dict = validate_feed)
print("After %d training step(s) ,validation accuracy using average model is %g " % (i,validate_acc))
list_test_acc.append(validate_acc)
# 产生这一轮使用的一个batch 的训练、数据,并运行训练过程。
xs,ys = mnist.train.next_batch(BATCH_SIZE)
sess.run(train_op, feed_dict={x:xs,y_:ys})
# 在训练结束之后,在测试数据上检测神经网络模型的最终正确率。
test_acc = sess.run(accuracy, feed_dict=test_feed)
print("After %d training step(s) ,test accuracy using average model is %g " % (TRAINING_STEPS,test_acc))
# ********************
list_test_acc.append(test_acc)
list_test_acc[0] = 0.974
xx = range(len(list_test_acc))
yy = list_test_acc
plt.plot(xx, yy, marker='o', mec='r', mfc='w',label=u'训练准确率曲线图')
plt.show()
# ********************
# 主程序入口。
def main(argv=None):
# 声明处理MNIST数据集的类,这个类在初始化时会自动下载数据。
mnist = input_data.read_data_sets('..\MNIST_data',one_hot=True)
train(mnist)
# TensorFlow 提供的一个主程序入口,tf.app.run 会调用上面定义的main 函数。
if __name__ == '__main__':
tf.app.run()
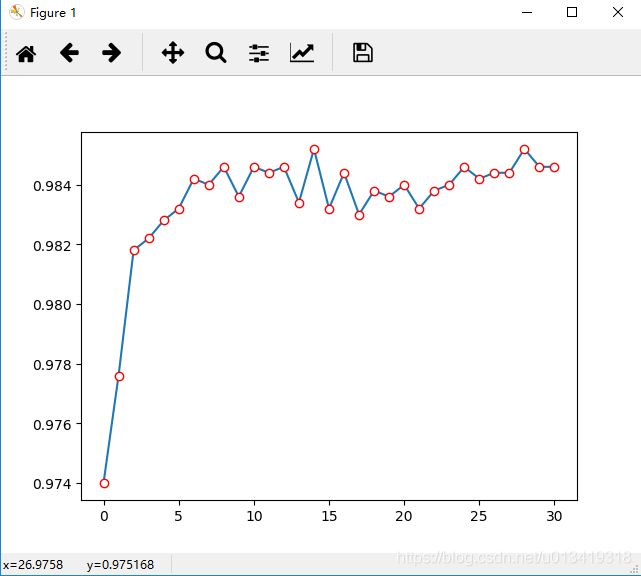
(2)运行结果
3,总结
运行结果可以看出,神经网络的训练效果在前期有明显的提升,训练后期逐渐趋于稳定。同时可以看到,利用神经网络实现的手写体数字识别的准确度比传统的机器学习算法的识别准确度有了巨大的提升。这也体现了神经网络在图像识别方面的优势。